23.1 图形的旋转培优练习2023-2024学年人教版九年级上册数学(无答案)
文档属性
| 名称 | 23.1 图形的旋转培优练习2023-2024学年人教版九年级上册数学(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 379.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 00:00:00 | ||
图片预览


文档简介
23.1 图形的旋转
一、选择题。
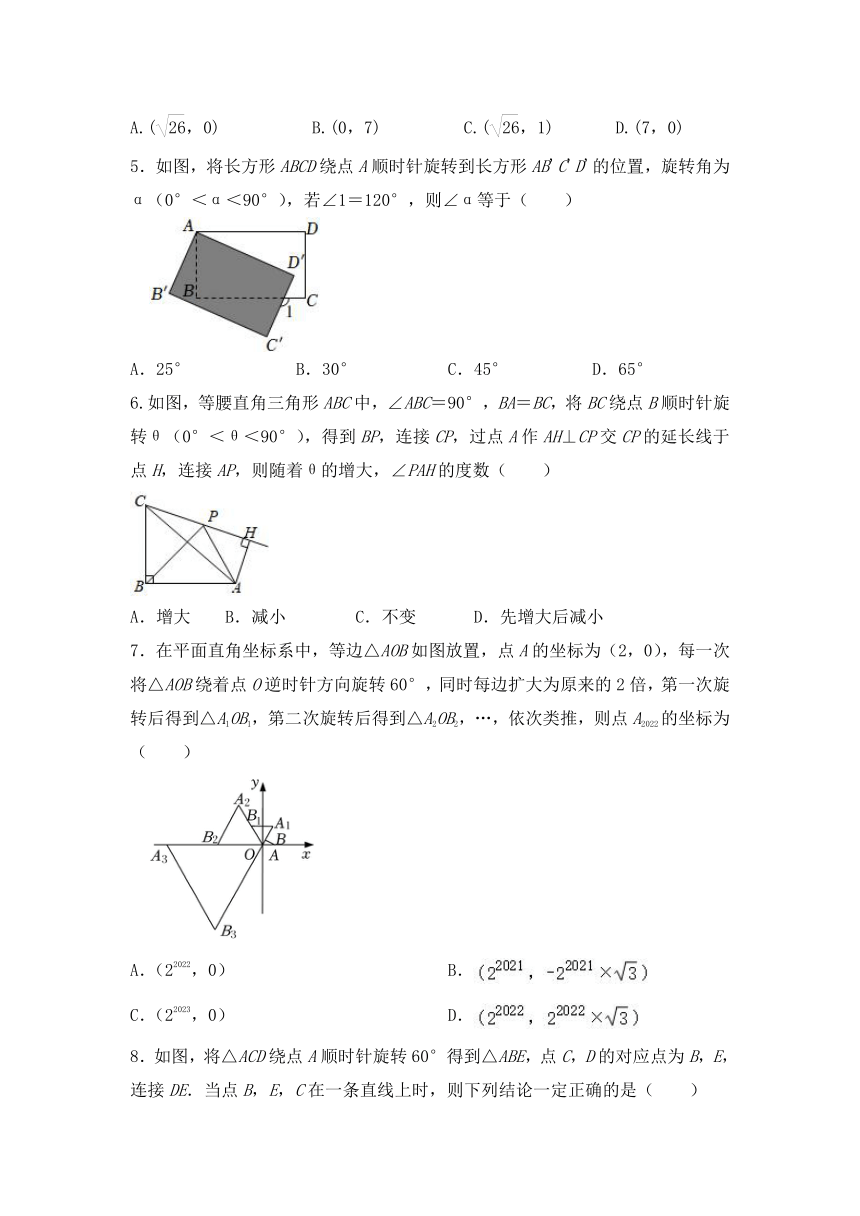
1.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别( )
A.4,30° B.2,60° C.1,30° D.3,60°
2.如图,在等腰直角△ABC中,∠BAC=90°,点D是△ABC所在平面上一点,且满足DB=3,DA=5,则CD的最小值为( )
A.5-3 B.5-3 C.2 D.1
3.如图,已知正方形ABCD,点E、F分别是AB、BC边上,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.下列结论正确的是( )
A.F是BM的中点 B.BE=BF
C.△EDF≌△MDF D.EF∥DM
4.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕C点顺时针方向旋转90°后,A点的坐标为( )
A.(,0) B.(0,7) C.(,1) D.(7,0)
5.如图,将长方形ABCD绕点A顺时针旋转到长方形AB'C'D'的位置,旋转角为α(0°<α<90°),若∠1=120°,则∠α等于( )
A.25° B.30° C.45° D.65°
6.如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则随着θ的增大,∠PAH的度数( )
A.增大 B.减小 C.不变 D.先增大后减小
7.在平面直角坐标系中,等边△AOB如图放置,点A的坐标为(2,0),每一次将△AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A1OB1,第二次旋转后得到△A2OB2,…,依次类推,则点A2022的坐标为( )
A.(22022,0) B.
C.(22023,0) D.
8.如图,将△ACD绕点A顺时针旋转60°得到△ABE,点C,D的对应点为B,E,连接DE.当点B,E,C在一条直线上时,则下列结论一定正确的是( )
A.AB=EC+DC B.AE=AC C.∠ADC=60° D.AE∥CD
9.如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10) C.(10,-3) D.(3,-10)
10.如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A. B.2 C.3 D.2
11.如图,在正方形中,、是射线上的动点,且,射线、分别交、延长线于、,连接,在下列结论中:①;②;③;④若,则,⑤,其中正确的结论有( )
个 B.个
C.个 D.个
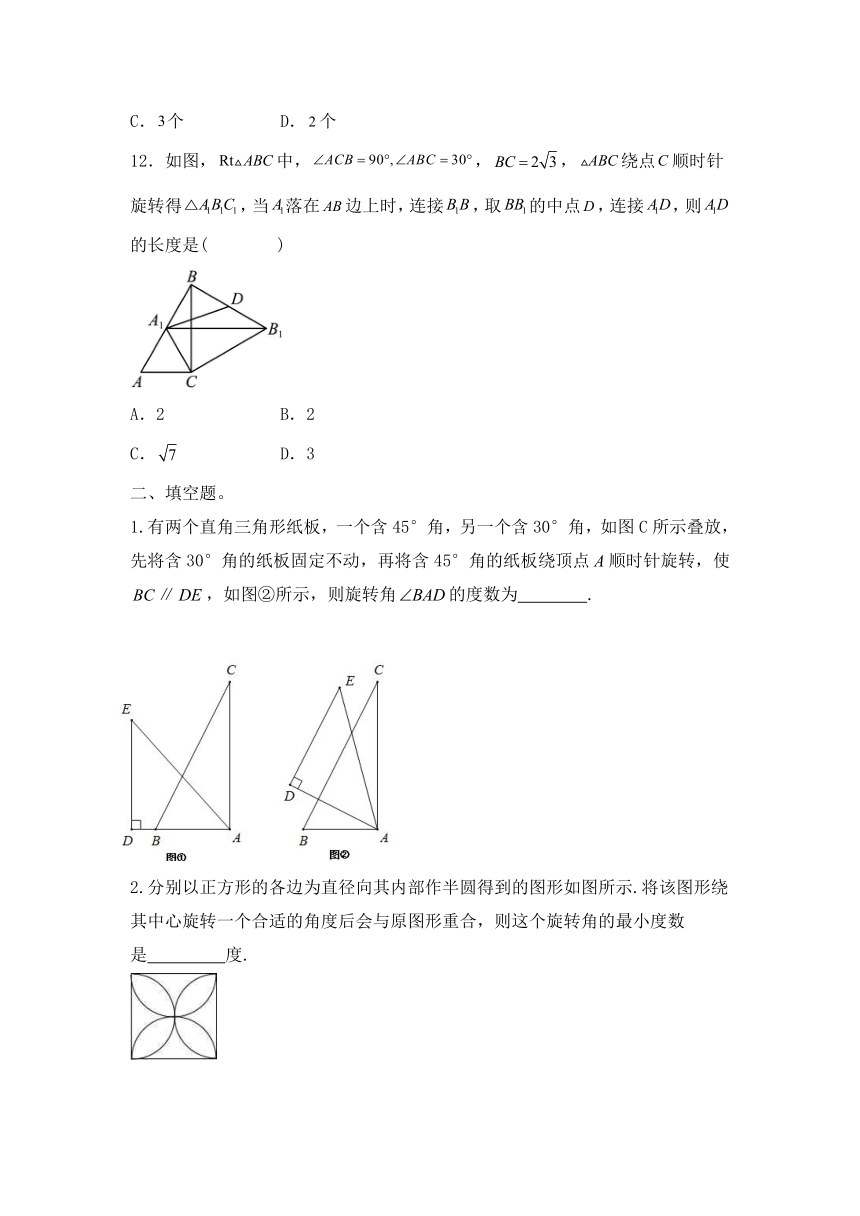
12.如图,中,,,绕点顺时针旋转得,当落在边上时,连接,取的中点,连接,则的长度是( )
A.2 B.2
C. D.3
二、填空题。
1.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图C所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点顺时针旋转,使∥,如图②所示,则旋转角的度数为 .
2.分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是 度.
32.如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为_____.
4.如图,正△ABO的边长为4,O为坐标原点,A在x轴上,△ABO沿x轴正方
向作无滑动的翻滚,经一次翻滚后得到△A1B1O,翻滚2022次后AB中点M坐标为 .
5.在中,,D是线段上的动点.连接,将绕点C逆时针旋转至的位置.连接,则的最大值为 _____.
6.如图,在△ABC中,∠BAC=105°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB=CB',则∠AB'C'的度数为 .
三、解答题。
1.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABG,连接EG.
(1)求证:△AEG≌△AEF;
(2)求证:EF2=DF2+BE2.
2.如图,在△ABC中,点E在边BC上,AE=AB,将线段AC绕点A逆时针旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
求证:EF=BC.
3.如图,把矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,使点E落在对角线BD上,连接DG,DF.
(1)若∠BAE=50°,求∠DGF的度数;
(2)求证:DF=DC.
4.如图,在△ABC中,AB=AC,D 是BC上一点,且AD=BD.将△ABD绕点A逆时针旋转得到△ACE.
(1)求证:AE∥BC;
(2)连结DE,判断四边形ABDE的形状,并说明理由.
5.如图,在△ABC中,将△ABC绕点C按顺时针方向旋转得△A1B1C.
(1)若∠ACB=90°,且A1B1∥BC,∠BCB1=40°,求∠A的大小;
(2)若BC=4,CA1=3,AB=5,求△A1B1C的周长.
6.如图,等腰△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A逆时针旋转一定角度α(45°<α≤90°)得到△ADE,点B、C的对应点分别是D、E.连结BD、CE交于点F,连结AD、CE交于点G.
(1)用含α的代数式表示∠AGC的度数;
(2)当AE∥BD时,求CF的长.
一、选择题。
1.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别( )
A.4,30° B.2,60° C.1,30° D.3,60°
2.如图,在等腰直角△ABC中,∠BAC=90°,点D是△ABC所在平面上一点,且满足DB=3,DA=5,则CD的最小值为( )
A.5-3 B.5-3 C.2 D.1
3.如图,已知正方形ABCD,点E、F分别是AB、BC边上,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.下列结论正确的是( )
A.F是BM的中点 B.BE=BF
C.△EDF≌△MDF D.EF∥DM
4.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕C点顺时针方向旋转90°后,A点的坐标为( )
A.(,0) B.(0,7) C.(,1) D.(7,0)
5.如图,将长方形ABCD绕点A顺时针旋转到长方形AB'C'D'的位置,旋转角为α(0°<α<90°),若∠1=120°,则∠α等于( )
A.25° B.30° C.45° D.65°
6.如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则随着θ的增大,∠PAH的度数( )
A.增大 B.减小 C.不变 D.先增大后减小
7.在平面直角坐标系中,等边△AOB如图放置,点A的坐标为(2,0),每一次将△AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A1OB1,第二次旋转后得到△A2OB2,…,依次类推,则点A2022的坐标为( )
A.(22022,0) B.
C.(22023,0) D.
8.如图,将△ACD绕点A顺时针旋转60°得到△ABE,点C,D的对应点为B,E,连接DE.当点B,E,C在一条直线上时,则下列结论一定正确的是( )
A.AB=EC+DC B.AE=AC C.∠ADC=60° D.AE∥CD
9.如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10) C.(10,-3) D.(3,-10)
10.如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A. B.2 C.3 D.2
11.如图,在正方形中,、是射线上的动点,且,射线、分别交、延长线于、,连接,在下列结论中:①;②;③;④若,则,⑤,其中正确的结论有( )
个 B.个
C.个 D.个
12.如图,中,,,绕点顺时针旋转得,当落在边上时,连接,取的中点,连接,则的长度是( )
A.2 B.2
C. D.3
二、填空题。
1.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图C所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点顺时针旋转,使∥,如图②所示,则旋转角的度数为 .
2.分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是 度.
32.如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为_____.
4.如图,正△ABO的边长为4,O为坐标原点,A在x轴上,△ABO沿x轴正方
向作无滑动的翻滚,经一次翻滚后得到△A1B1O,翻滚2022次后AB中点M坐标为 .
5.在中,,D是线段上的动点.连接,将绕点C逆时针旋转至的位置.连接,则的最大值为 _____.
6.如图,在△ABC中,∠BAC=105°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB=CB',则∠AB'C'的度数为 .
三、解答题。
1.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABG,连接EG.
(1)求证:△AEG≌△AEF;
(2)求证:EF2=DF2+BE2.
2.如图,在△ABC中,点E在边BC上,AE=AB,将线段AC绕点A逆时针旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
求证:EF=BC.
3.如图,把矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,使点E落在对角线BD上,连接DG,DF.
(1)若∠BAE=50°,求∠DGF的度数;
(2)求证:DF=DC.
4.如图,在△ABC中,AB=AC,D 是BC上一点,且AD=BD.将△ABD绕点A逆时针旋转得到△ACE.
(1)求证:AE∥BC;
(2)连结DE,判断四边形ABDE的形状,并说明理由.
5.如图,在△ABC中,将△ABC绕点C按顺时针方向旋转得△A1B1C.
(1)若∠ACB=90°,且A1B1∥BC,∠BCB1=40°,求∠A的大小;
(2)若BC=4,CA1=3,AB=5,求△A1B1C的周长.
6.如图,等腰△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A逆时针旋转一定角度α(45°<α≤90°)得到△ADE,点B、C的对应点分别是D、E.连结BD、CE交于点F,连结AD、CE交于点G.
(1)用含α的代数式表示∠AGC的度数;
(2)当AE∥BD时,求CF的长.
同课章节目录
