第1章 一元二次方程(单元统考测试)2023-2024学年苏科版九年级数学上册(含解析)
文档属性
| 名称 | 第1章 一元二次方程(单元统考测试)2023-2024学年苏科版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 93.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 19:09:57 | ||
图片预览




文档简介
第1章 一元二次方程(单元统考测试)
苏科新版九年级上学期数学
一.选择题(共10小题)
1.下列方程是关于x的一元二次方程的是( )
A. B.2x2﹣y+6=0
C.ax2+bx+c=0 D.
2.将一元二次方程3x2=﹣4+2x化为一般形式后,二次项系数和一次项系数分别是( )
A.3,﹣2 B.﹣3,2 C.3,2 D.﹣3,﹣2
3.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3 B.(x+2)2=11 C.(x﹣2)2=3 D.(x﹣2)2=11
4.一元二次方程x2﹣4x+2=0根的情况是( )
A.无实数根 B.有两个正根
C.有一个正根,一个负根 D.有两个负根
5.方程x(x﹣6)﹣6+x=0的解是( )
A.x1=6,x2=﹣1 B.x1=6,x2=1
C.x1=﹣6,x2=﹣1 D.x1=﹣6,x2=1
6.若实数x,y满足(x+y)(x+y﹣1)=2,则x+y的值为( )
A.﹣1 B.2 C.﹣1或2 D.﹣2或1
7.某市组织一次足球联赛,赛制为单循环形式(每两队之间都要赛一场),共比赛了21场,设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x﹣1)=21 B.x(x+1)=21
C.x(x﹣1)=21 D.x(x+1)=21
8.若关于x的一元二次方程ax2+bx+5=0的一个根是x=﹣1,则2018﹣a+b的值是( )
A.2013 B.2016 C.2023 D.2021
9.已知a,b,c满足a2+4b=﹣7,b2﹣2c=3,c2+2a=﹣2,则a+b﹣c的值为( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
10.一元二次方程x2﹣8x﹣a=0的两实数根都是整数,则下列选项中a可以取的值是( )
A.12 B.16 C.20 D.24
二.填空题(共7小题)
11.是关于x的一元二次方程,则a的值是 .
12.若代数式x2﹣4x+1的值与﹣3x+2的值相等,则x的值为 .
13.关于x的方程a(x+k)2+2023=0的解是x1=﹣2,x2=1(a、k、b均为常数,a≠0).
问题:
(1)关于x的方程a(x+k+2)2+2023=0的根是 ;
(2)关于x的方程a(x﹣k+2)2+2023=0的根为 .
14.杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除算法》):直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.解答这个问题可知长为 步.
15.已知α,β是方程x2+3x﹣1=0的两个实数根,则3α3﹣10β2= .
16.已知a是正整数,且使得关于x的一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0至少有一个整数根,则a的值为 .
17.已知①x2+ax+b=0,②x2+bx+c=0,③x2+cx+a=0,a≠b≠c,方程①②有公共根p,②③有公共根q,①③有公共根r,则abc= .
三.解答题(共5小题)
18.当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2.
(1)是一元二次方程;
(2)是一元一次方程.
19.求证:当关于x的一元二次方程x2+2x=m+9没有实数根时,关于y的一元二次方程y2+my﹣2m=﹣5一定有两个不相等的实数根.
20.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,求该长方体的底面宽,若该长方体的底面宽为x米:
(1)用含x的代数式分别表示出该长方体的底面长和容积.
(2)请列出关于x的方程.
21.先阅读材料,然后按照要求答题.
阅读材料:为了解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,(x2﹣1)2=y2,则原方程可化为:y2﹣5y+4=0①
解得:y1=1,y2=4
当y=1时,x2﹣1=1,x2=2,
∴x=±,
当y=4时,x2﹣1=4,x2=5,
∴x=±,
∴原方程的解为:x1=,x2=﹣,x3=,x4=﹣,
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用 法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决问题:若(m2+n2﹣2)(m2+n2)=8,求m2+n2的值.
22.我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用,例如:试求二次三项式x2+4x+5最小值.解:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1,即x2+4x+5的最小值是1.试利用“配方法”解决下列问题:
(1)已知y=x2﹣6x+12,求y的最小值.
(2)比较代数式3x2﹣x+2与2x2+3x﹣6的大小,并说明理由.
知识迁移:
(3)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P在AC边上以2cm/s的速度从点A向C移动,点Q在CB边上以1cm/s的速度从点C向点B移动.若点P,Q同时出发,且当一点移动到终点时,另一点也随之停止,设四边形APQB的面积为Scm2,运动时间为t秒,求S的最小值.
第1章 一元二次方程(单元统考测试)苏科新版九年级上学期数学
参考答案与试题解析
一.选择题(共10小题)
1.下列方程是关于x的一元二次方程的是( )
A. B.2x2﹣y+6=0
C.ax2+bx+c=0 D.
【答案】A
【解答】解:A、是关于x的一元二次方程,故本选项符合题意;
C、是关于x,y的二元二次方程,故本选项不符合题意;
C、当a=0时不是关于x的一元二次方程,故本选项不符合题意;
D、是关于x的分式方程,故本选项不符合题意;
故选:A.
2.将一元二次方程3x2=﹣4+2x化为一般形式后,二次项系数和一次项系数分别是( )
A.3,﹣2 B.﹣3,2 C.3,2 D.﹣3,﹣2
【答案】A
【解答】解:∵将原方程转化成一般式为3x2﹣2x+4=0,
∴二次项系数为3,一次项系数为﹣2.
故选:A.
3.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3 B.(x+2)2=11 C.(x﹣2)2=3 D.(x﹣2)2=11
【答案】D
【解答】解:∵x2﹣4x﹣7=0,
∴x2﹣4x+4=11,
∴(x﹣2)2=11,
故选:D.
4.一元二次方程x2﹣4x+2=0根的情况是( )
A.无实数根 B.有两个正根
C.有一个正根,一个负根 D.有两个负根
【答案】B
【解答】解:x2﹣4x+2=0,
∵Δ=(﹣4)2﹣4×1×2=8>0,且x1+x2=4>0,x1 x2=2>0,
∴有两个正根,
故选:B.
5.方程x(x﹣6)﹣6+x=0的解是( )
A.x1=6,x2=﹣1 B.x1=6,x2=1
C.x1=﹣6,x2=﹣1 D.x1=﹣6,x2=1
【答案】A
【解答】解:∵x(x﹣6)﹣6+x=0,
∴x(x﹣6)+(x﹣6)=0,
则(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
解得x1=6,x2=﹣1,
故选:A.
6.若实数x,y满足(x+y)(x+y﹣1)=2,则x+y的值为( )
A.﹣1 B.2 C.﹣1或2 D.﹣2或1
【答案】C
【解答】解:设x+y=a,
方程整理得:a(a﹣1)=2,
整理得:a2﹣a﹣2=0,即(a﹣2)(a+1)=0,
解得:a=2或a=﹣1,
则x+y=2或﹣1.
故选:C.
7.某市组织一次足球联赛,赛制为单循环形式(每两队之间都要赛一场),共比赛了21场,设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x﹣1)=21 B.x(x+1)=21
C.x(x﹣1)=21 D.x(x+1)=21
【答案】C
【解答】解:设有x个球队参加比赛,
依题意得1+2+3+…+x﹣1=21,
即x(x﹣1)=21.
故选:C.
8.若关于x的一元二次方程ax2+bx+5=0的一个根是x=﹣1,则2018﹣a+b的值是( )
A.2013 B.2016 C.2023 D.2021
【答案】C
【解答】解:把x=﹣1代入方程ax2+bx+5=0得a﹣b+5=0,
所以a﹣b=﹣5,
所以2018﹣a+b=2018﹣(a﹣b)=2018﹣(﹣5)=2023.
故选:C.
9.已知a,b,c满足a2+4b=﹣7,b2﹣2c=3,c2+2a=﹣2,则a+b﹣c的值为( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
【答案】A
【解答】解:∵a2+4b=﹣7,b2﹣2c=3,c2+2a=﹣2,
∴a2+4b+b2﹣2c+c2+2a=﹣6,
∴a2+2a+1+b2+4b+4+c2﹣2c+1=0,即(a+1)2+(b+2)2+(c﹣1)2=0,
∴a=﹣1,b=﹣2,c=1,
∴a+b﹣c=﹣1﹣2﹣1=﹣4;
故选A.
10.一元二次方程x2﹣8x﹣a=0的两实数根都是整数,则下列选项中a可以取的值是( )
A.12 B.16 C.20 D.24
【答案】C
【解答】解:当a=12时,方程为x2﹣8x﹣12=0,解得不是整数,故A选项不符合题意;
当a=16时,方程为x2﹣8x﹣16=0,解得不是整数,故B选项不符合题意;
当a=20时,方程为x2﹣8x﹣20=0,解得x=10或x=﹣2是整数,故C选项符合题意;
当a=24时,方程为x2﹣8x﹣24=0,解得不是整数,故D选项不符合题意;
解法二:x=4±,
由选项可知,a=20,符合题意.
故选:C.
二.填空题(共7小题)
11.是关于x的一元二次方程,则a的值是 ﹣2 .
【答案】﹣2.
【解答】解:∵(a﹣2)x+3x﹣1=0是关于x的一元二次方程,
∴a2﹣2=2,a﹣2≠0,
解得:a=﹣2.
故答案为:﹣2.
12.若代数式x2﹣4x+1的值与﹣3x+2的值相等,则x的值为 x1=,x2= .
【答案】x1=,x2=.
【解答】解:根据题意得x2﹣4x+1=﹣3x+2,
整理得x2﹣x﹣1=0,
∵Δ=(﹣1)2﹣4×(﹣1)=5>0,
∴x==,
∴x1=,x2=.
故答案为:x1=,x2=.
13.关于x的方程a(x+k)2+2023=0的解是x1=﹣2,x2=1(a、k、b均为常数,a≠0).
问题:
(1)关于x的方程a(x+k+2)2+2023=0的根是 x1=﹣4,x2=﹣1 ;
(2)关于x的方程a(x﹣k+2)2+2023=0的根为 x1=0,x2=﹣3 .
【答案】(1)x1=﹣4,x2=﹣1;
(2)x1=0,x2=﹣3.
【解答】解:(1)∵方程a(x+k)2+2023=0的解是x1=﹣2,x2=1,
∵a(x+k+2)2+2023=0,
∴x+2=﹣2,x+2=1,
解得x1=﹣4,x2=﹣1,
故答案为:x1=﹣4,x2=﹣1.
(2)∵方程a(x+k)2+2023=0的解是x1=﹣2,x2=1,
∵a(x﹣k+2)2+2023=0,
∴x+2=﹣1,x+2=2,
∴x1=0,x2=﹣3,
故答案为:x1=0,x2=﹣3.
14.杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除算法》):直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.解答这个问题可知长为 36 步.
【答案】36.
【解答】解:设长为x步,则宽为(x﹣12)步,
依题意得:x(x﹣12)=864,
整理得:x2﹣12x﹣864=0,
解得:x1=36,x2=﹣24(不合题意,舍去).
故答案为:36.
15.已知α,β是方程x2+3x﹣1=0的两个实数根,则3α3﹣10β2= ﹣109 .
【答案】﹣109.
【解答】解:∵α,β是方程x2+3x﹣1=0的两个实数根,
∴α2+3α﹣1=0,β2+3β﹣1=0,α+β=﹣3,
∴α2=﹣3a+1,β2=﹣3β+1,
∴α3=﹣3α2+α=﹣3(﹣3α+1)+α=9α﹣3+2α=10α﹣3,
则3α3﹣10β2=3(10α﹣3)﹣10(﹣3β+1)=30α﹣9+30β﹣10=30(α+β)﹣19=﹣109,
故答案为:﹣109.
16.已知a是正整数,且使得关于x的一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0至少有一个整数根,则a的值为 2 .
【答案】2.
【解答】解:由题意知,a≠0,
Δ=[2(2a﹣3)]2﹣4a[4(a﹣2)]=36﹣16a≥0,
∵关于x的一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0至少有一个整数根,
∴36﹣16a为完全平方数,
又∵a是正整数,
∴当a=2时,36﹣16a=36﹣16×2=4=22是完全平方数,
此时一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0可整理为:
x2+x=0,
解得x=1或0,有整数根,
∴a的值为2符合题意,
故答案为:2.
17.已知①x2+ax+b=0,②x2+bx+c=0,③x2+cx+a=0,a≠b≠c,方程①②有公共根p,②③有公共根q,①③有公共根r,则abc= 1 .
【答案】1.
【解答】解:由题意得:p2+ap+b=0,p2+bp+c=0.
∴(a﹣b)p+b﹣c=0,
∴p=.
同理,q=,r=.
∴pqr=﹣1.
若p=q=r时,则有p=q=r=﹣1,
将其代入方程,则有.
∴a=b=c,与题设矛盾.
∴p、q、r互不相等.
∵p、q、r互不相等.若p=q,则p、q是①③公共根,于是p=q=r=﹣1.代入方程①②③,得
.
三式相加,有0=﹣3,矛盾.
∴①的两根为p、r.②的两根为p、q,③的两根为q、r.
由根与系数的关系,有a=qr,b=pr,c=pq,
∴abc=(pqr)2=1.
故答案为:1.
三.解答题(共5小题)
18.当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2.
(1)是一元二次方程;
(2)是一元一次方程.
【答案】(1)m≠±1;(2)m=﹣1.
【解答】解:(1)∵(m2+2)x2+(m﹣1)x﹣4=3x2是一元二次方程,
∴m2+2≠3,
解得m≠±1;
(2)∵(m2+2)x2+(m﹣1)x﹣4=3x2是一元一次方程,
∴,
解得m=﹣1.
19.求证:当关于x的一元二次方程x2+2x=m+9没有实数根时,关于y的一元二次方程y2+my﹣2m=﹣5一定有两个不相等的实数根.
【答案】证明见解析.
【解答】解:一元二次方程x2+2x=m+9化为:x2+2x﹣m﹣9=0,
∵关于x的一元二次方程x2+2x=m+9没有实数根,
∴△1=22﹣4(﹣m﹣9)<0,解得:m<﹣10,
关于y的一元二次方程y2+my﹣2m=﹣5化为:y2+my﹣2m+5=0,
∴△2=m2﹣4(﹣2m+5)=m2+8m﹣20=(m+4)2﹣36,
∵m<﹣10,
∴(m+4)2>36,
∴(m+4)2﹣36>0,即△2>0,
∴关于y的一元二次方程y2+my﹣2m=﹣5一定有两个不相等的实数根.
20.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,求该长方体的底面宽,若该长方体的底面宽为x米:
(1)用含x的代数式分别表示出该长方体的底面长和容积.
(2)请列出关于x的方程.
【答案】见试题解答内容
【解答】解:(1)长方体运输箱底面的宽为xm,则长为(x+2)m.
容积为x(x+2)×1=x2+2x;
(2)x2+2x=15.
21.先阅读材料,然后按照要求答题.
阅读材料:为了解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,(x2﹣1)2=y2,则原方程可化为:y2﹣5y+4=0①
解得:y1=1,y2=4
当y=1时,x2﹣1=1,x2=2,
∴x=±,
当y=4时,x2﹣1=4,x2=5,
∴x=±,
∴原方程的解为:x1=,x2=﹣,x3=,x4=﹣,
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用 换元 法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决问题:若(m2+n2﹣2)(m2+n2)=8,求m2+n2的值.
【答案】(1)换元;
(2)4.
【解答】解:(1)上述解题过程,在由原方程得到方程①的过程中,利用换元法达到了解方程的目的,体现了转化的数学思想,
故答案为:换元;
(2)(m2+n2﹣2)(m2+n2)=8,
设m2+n2=x,
则原方程化为:(x﹣2)x=8,
即x2﹣2x﹣8=0,
解得:x=4或﹣2,
当x=4时,m2+n2=4,
当x=﹣2时,m2+n2=﹣1,
因为不论m、n为何值,m2+n2≥0,
所以m2+n2=﹣2不符合,舍去,
即m2+n2=4.
22.我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用,例如:试求二次三项式x2+4x+5最小值.解:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1,即x2+4x+5的最小值是1.试利用“配方法”解决下列问题:
(1)已知y=x2﹣6x+12,求y的最小值.
(2)比较代数式3x2﹣x+2与2x2+3x﹣6的大小,并说明理由.
知识迁移:
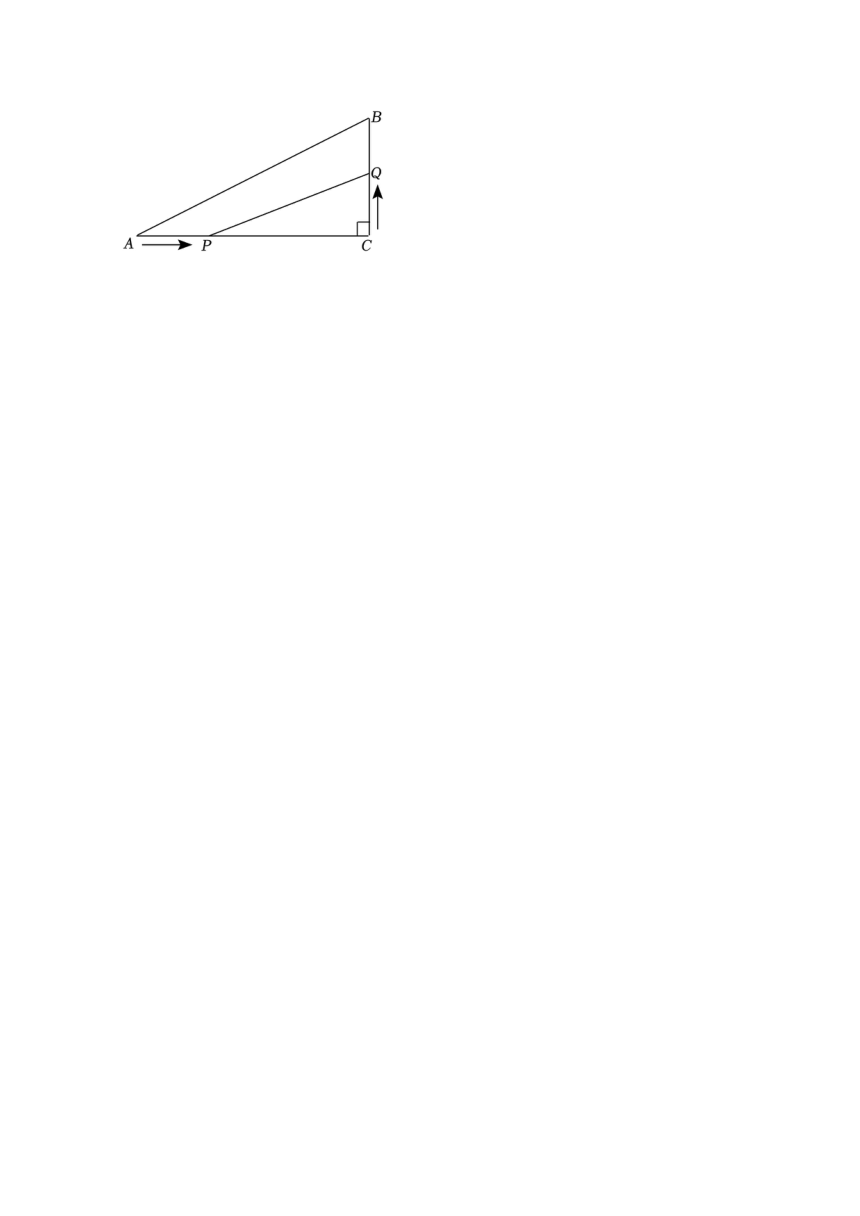
(3)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P在AC边上以2cm/s的速度从点A向C移动,点Q在CB边上以1cm/s的速度从点C向点B移动.若点P,Q同时出发,且当一点移动到终点时,另一点也随之停止,设四边形APQB的面积为Scm2,运动时间为t秒,求S的最小值.
【答案】(1)3;
(2)3x2﹣x+2>2x2+3x﹣6;
(3)5.
【解答】解:(1)∵y=x2﹣6x+12,
∴y=(x﹣3)2+3,
∴y的最小值为3;
(2)3x2﹣x+2﹣(2x2+3x﹣6)
=3x2﹣x+2﹣2x2﹣3x+6
=x2﹣4x+8
=(x﹣2)2+4
∵(x﹣2)2+4>0
∴3x2﹣x+2>2x2+3x﹣6;
(3)根据题意可得:
S=S△ABC﹣S△PQC,
S=×4×3﹣(4﹣2t)t,
S=6﹣2t+t2,
S=(t﹣1)2+5,
∴S的最小值为5.
苏科新版九年级上学期数学
一.选择题(共10小题)
1.下列方程是关于x的一元二次方程的是( )
A. B.2x2﹣y+6=0
C.ax2+bx+c=0 D.
2.将一元二次方程3x2=﹣4+2x化为一般形式后,二次项系数和一次项系数分别是( )
A.3,﹣2 B.﹣3,2 C.3,2 D.﹣3,﹣2
3.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3 B.(x+2)2=11 C.(x﹣2)2=3 D.(x﹣2)2=11
4.一元二次方程x2﹣4x+2=0根的情况是( )
A.无实数根 B.有两个正根
C.有一个正根,一个负根 D.有两个负根
5.方程x(x﹣6)﹣6+x=0的解是( )
A.x1=6,x2=﹣1 B.x1=6,x2=1
C.x1=﹣6,x2=﹣1 D.x1=﹣6,x2=1
6.若实数x,y满足(x+y)(x+y﹣1)=2,则x+y的值为( )
A.﹣1 B.2 C.﹣1或2 D.﹣2或1
7.某市组织一次足球联赛,赛制为单循环形式(每两队之间都要赛一场),共比赛了21场,设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x﹣1)=21 B.x(x+1)=21
C.x(x﹣1)=21 D.x(x+1)=21
8.若关于x的一元二次方程ax2+bx+5=0的一个根是x=﹣1,则2018﹣a+b的值是( )
A.2013 B.2016 C.2023 D.2021
9.已知a,b,c满足a2+4b=﹣7,b2﹣2c=3,c2+2a=﹣2,则a+b﹣c的值为( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
10.一元二次方程x2﹣8x﹣a=0的两实数根都是整数,则下列选项中a可以取的值是( )
A.12 B.16 C.20 D.24
二.填空题(共7小题)
11.是关于x的一元二次方程,则a的值是 .
12.若代数式x2﹣4x+1的值与﹣3x+2的值相等,则x的值为 .
13.关于x的方程a(x+k)2+2023=0的解是x1=﹣2,x2=1(a、k、b均为常数,a≠0).
问题:
(1)关于x的方程a(x+k+2)2+2023=0的根是 ;
(2)关于x的方程a(x﹣k+2)2+2023=0的根为 .
14.杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除算法》):直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.解答这个问题可知长为 步.
15.已知α,β是方程x2+3x﹣1=0的两个实数根,则3α3﹣10β2= .
16.已知a是正整数,且使得关于x的一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0至少有一个整数根,则a的值为 .
17.已知①x2+ax+b=0,②x2+bx+c=0,③x2+cx+a=0,a≠b≠c,方程①②有公共根p,②③有公共根q,①③有公共根r,则abc= .
三.解答题(共5小题)
18.当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2.
(1)是一元二次方程;
(2)是一元一次方程.
19.求证:当关于x的一元二次方程x2+2x=m+9没有实数根时,关于y的一元二次方程y2+my﹣2m=﹣5一定有两个不相等的实数根.
20.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,求该长方体的底面宽,若该长方体的底面宽为x米:
(1)用含x的代数式分别表示出该长方体的底面长和容积.
(2)请列出关于x的方程.
21.先阅读材料,然后按照要求答题.
阅读材料:为了解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,(x2﹣1)2=y2,则原方程可化为:y2﹣5y+4=0①
解得:y1=1,y2=4
当y=1时,x2﹣1=1,x2=2,
∴x=±,
当y=4时,x2﹣1=4,x2=5,
∴x=±,
∴原方程的解为:x1=,x2=﹣,x3=,x4=﹣,
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用 法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决问题:若(m2+n2﹣2)(m2+n2)=8,求m2+n2的值.
22.我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用,例如:试求二次三项式x2+4x+5最小值.解:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1,即x2+4x+5的最小值是1.试利用“配方法”解决下列问题:
(1)已知y=x2﹣6x+12,求y的最小值.
(2)比较代数式3x2﹣x+2与2x2+3x﹣6的大小,并说明理由.
知识迁移:
(3)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P在AC边上以2cm/s的速度从点A向C移动,点Q在CB边上以1cm/s的速度从点C向点B移动.若点P,Q同时出发,且当一点移动到终点时,另一点也随之停止,设四边形APQB的面积为Scm2,运动时间为t秒,求S的最小值.
第1章 一元二次方程(单元统考测试)苏科新版九年级上学期数学
参考答案与试题解析
一.选择题(共10小题)
1.下列方程是关于x的一元二次方程的是( )
A. B.2x2﹣y+6=0
C.ax2+bx+c=0 D.
【答案】A
【解答】解:A、是关于x的一元二次方程,故本选项符合题意;
C、是关于x,y的二元二次方程,故本选项不符合题意;
C、当a=0时不是关于x的一元二次方程,故本选项不符合题意;
D、是关于x的分式方程,故本选项不符合题意;
故选:A.
2.将一元二次方程3x2=﹣4+2x化为一般形式后,二次项系数和一次项系数分别是( )
A.3,﹣2 B.﹣3,2 C.3,2 D.﹣3,﹣2
【答案】A
【解答】解:∵将原方程转化成一般式为3x2﹣2x+4=0,
∴二次项系数为3,一次项系数为﹣2.
故选:A.
3.用配方法解方程x2﹣4x﹣7=0,可变形为( )
A.(x+2)2=3 B.(x+2)2=11 C.(x﹣2)2=3 D.(x﹣2)2=11
【答案】D
【解答】解:∵x2﹣4x﹣7=0,
∴x2﹣4x+4=11,
∴(x﹣2)2=11,
故选:D.
4.一元二次方程x2﹣4x+2=0根的情况是( )
A.无实数根 B.有两个正根
C.有一个正根,一个负根 D.有两个负根
【答案】B
【解答】解:x2﹣4x+2=0,
∵Δ=(﹣4)2﹣4×1×2=8>0,且x1+x2=4>0,x1 x2=2>0,
∴有两个正根,
故选:B.
5.方程x(x﹣6)﹣6+x=0的解是( )
A.x1=6,x2=﹣1 B.x1=6,x2=1
C.x1=﹣6,x2=﹣1 D.x1=﹣6,x2=1
【答案】A
【解答】解:∵x(x﹣6)﹣6+x=0,
∴x(x﹣6)+(x﹣6)=0,
则(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
解得x1=6,x2=﹣1,
故选:A.
6.若实数x,y满足(x+y)(x+y﹣1)=2,则x+y的值为( )
A.﹣1 B.2 C.﹣1或2 D.﹣2或1
【答案】C
【解答】解:设x+y=a,
方程整理得:a(a﹣1)=2,
整理得:a2﹣a﹣2=0,即(a﹣2)(a+1)=0,
解得:a=2或a=﹣1,
则x+y=2或﹣1.
故选:C.
7.某市组织一次足球联赛,赛制为单循环形式(每两队之间都要赛一场),共比赛了21场,设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x﹣1)=21 B.x(x+1)=21
C.x(x﹣1)=21 D.x(x+1)=21
【答案】C
【解答】解:设有x个球队参加比赛,
依题意得1+2+3+…+x﹣1=21,
即x(x﹣1)=21.
故选:C.
8.若关于x的一元二次方程ax2+bx+5=0的一个根是x=﹣1,则2018﹣a+b的值是( )
A.2013 B.2016 C.2023 D.2021
【答案】C
【解答】解:把x=﹣1代入方程ax2+bx+5=0得a﹣b+5=0,
所以a﹣b=﹣5,
所以2018﹣a+b=2018﹣(a﹣b)=2018﹣(﹣5)=2023.
故选:C.
9.已知a,b,c满足a2+4b=﹣7,b2﹣2c=3,c2+2a=﹣2,则a+b﹣c的值为( )
A.﹣4 B.﹣5 C.﹣6 D.﹣7
【答案】A
【解答】解:∵a2+4b=﹣7,b2﹣2c=3,c2+2a=﹣2,
∴a2+4b+b2﹣2c+c2+2a=﹣6,
∴a2+2a+1+b2+4b+4+c2﹣2c+1=0,即(a+1)2+(b+2)2+(c﹣1)2=0,
∴a=﹣1,b=﹣2,c=1,
∴a+b﹣c=﹣1﹣2﹣1=﹣4;
故选A.
10.一元二次方程x2﹣8x﹣a=0的两实数根都是整数,则下列选项中a可以取的值是( )
A.12 B.16 C.20 D.24
【答案】C
【解答】解:当a=12时,方程为x2﹣8x﹣12=0,解得不是整数,故A选项不符合题意;
当a=16时,方程为x2﹣8x﹣16=0,解得不是整数,故B选项不符合题意;
当a=20时,方程为x2﹣8x﹣20=0,解得x=10或x=﹣2是整数,故C选项符合题意;
当a=24时,方程为x2﹣8x﹣24=0,解得不是整数,故D选项不符合题意;
解法二:x=4±,
由选项可知,a=20,符合题意.
故选:C.
二.填空题(共7小题)
11.是关于x的一元二次方程,则a的值是 ﹣2 .
【答案】﹣2.
【解答】解:∵(a﹣2)x+3x﹣1=0是关于x的一元二次方程,
∴a2﹣2=2,a﹣2≠0,
解得:a=﹣2.
故答案为:﹣2.
12.若代数式x2﹣4x+1的值与﹣3x+2的值相等,则x的值为 x1=,x2= .
【答案】x1=,x2=.
【解答】解:根据题意得x2﹣4x+1=﹣3x+2,
整理得x2﹣x﹣1=0,
∵Δ=(﹣1)2﹣4×(﹣1)=5>0,
∴x==,
∴x1=,x2=.
故答案为:x1=,x2=.
13.关于x的方程a(x+k)2+2023=0的解是x1=﹣2,x2=1(a、k、b均为常数,a≠0).
问题:
(1)关于x的方程a(x+k+2)2+2023=0的根是 x1=﹣4,x2=﹣1 ;
(2)关于x的方程a(x﹣k+2)2+2023=0的根为 x1=0,x2=﹣3 .
【答案】(1)x1=﹣4,x2=﹣1;
(2)x1=0,x2=﹣3.
【解答】解:(1)∵方程a(x+k)2+2023=0的解是x1=﹣2,x2=1,
∵a(x+k+2)2+2023=0,
∴x+2=﹣2,x+2=1,
解得x1=﹣4,x2=﹣1,
故答案为:x1=﹣4,x2=﹣1.
(2)∵方程a(x+k)2+2023=0的解是x1=﹣2,x2=1,
∵a(x﹣k+2)2+2023=0,
∴x+2=﹣1,x+2=2,
∴x1=0,x2=﹣3,
故答案为:x1=0,x2=﹣3.
14.杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除算法》):直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.解答这个问题可知长为 36 步.
【答案】36.
【解答】解:设长为x步,则宽为(x﹣12)步,
依题意得:x(x﹣12)=864,
整理得:x2﹣12x﹣864=0,
解得:x1=36,x2=﹣24(不合题意,舍去).
故答案为:36.
15.已知α,β是方程x2+3x﹣1=0的两个实数根,则3α3﹣10β2= ﹣109 .
【答案】﹣109.
【解答】解:∵α,β是方程x2+3x﹣1=0的两个实数根,
∴α2+3α﹣1=0,β2+3β﹣1=0,α+β=﹣3,
∴α2=﹣3a+1,β2=﹣3β+1,
∴α3=﹣3α2+α=﹣3(﹣3α+1)+α=9α﹣3+2α=10α﹣3,
则3α3﹣10β2=3(10α﹣3)﹣10(﹣3β+1)=30α﹣9+30β﹣10=30(α+β)﹣19=﹣109,
故答案为:﹣109.
16.已知a是正整数,且使得关于x的一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0至少有一个整数根,则a的值为 2 .
【答案】2.
【解答】解:由题意知,a≠0,
Δ=[2(2a﹣3)]2﹣4a[4(a﹣2)]=36﹣16a≥0,
∵关于x的一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0至少有一个整数根,
∴36﹣16a为完全平方数,
又∵a是正整数,
∴当a=2时,36﹣16a=36﹣16×2=4=22是完全平方数,
此时一元二次方程ax2+2(2a﹣3)x+4(a﹣2)=0可整理为:
x2+x=0,
解得x=1或0,有整数根,
∴a的值为2符合题意,
故答案为:2.
17.已知①x2+ax+b=0,②x2+bx+c=0,③x2+cx+a=0,a≠b≠c,方程①②有公共根p,②③有公共根q,①③有公共根r,则abc= 1 .
【答案】1.
【解答】解:由题意得:p2+ap+b=0,p2+bp+c=0.
∴(a﹣b)p+b﹣c=0,
∴p=.
同理,q=,r=.
∴pqr=﹣1.
若p=q=r时,则有p=q=r=﹣1,
将其代入方程,则有.
∴a=b=c,与题设矛盾.
∴p、q、r互不相等.
∵p、q、r互不相等.若p=q,则p、q是①③公共根,于是p=q=r=﹣1.代入方程①②③,得
.
三式相加,有0=﹣3,矛盾.
∴①的两根为p、r.②的两根为p、q,③的两根为q、r.
由根与系数的关系,有a=qr,b=pr,c=pq,
∴abc=(pqr)2=1.
故答案为:1.
三.解答题(共5小题)
18.当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2.
(1)是一元二次方程;
(2)是一元一次方程.
【答案】(1)m≠±1;(2)m=﹣1.
【解答】解:(1)∵(m2+2)x2+(m﹣1)x﹣4=3x2是一元二次方程,
∴m2+2≠3,
解得m≠±1;
(2)∵(m2+2)x2+(m﹣1)x﹣4=3x2是一元一次方程,
∴,
解得m=﹣1.
19.求证:当关于x的一元二次方程x2+2x=m+9没有实数根时,关于y的一元二次方程y2+my﹣2m=﹣5一定有两个不相等的实数根.
【答案】证明见解析.
【解答】解:一元二次方程x2+2x=m+9化为:x2+2x﹣m﹣9=0,
∵关于x的一元二次方程x2+2x=m+9没有实数根,
∴△1=22﹣4(﹣m﹣9)<0,解得:m<﹣10,
关于y的一元二次方程y2+my﹣2m=﹣5化为:y2+my﹣2m+5=0,
∴△2=m2﹣4(﹣2m+5)=m2+8m﹣20=(m+4)2﹣36,
∵m<﹣10,
∴(m+4)2>36,
∴(m+4)2﹣36>0,即△2>0,
∴关于y的一元二次方程y2+my﹣2m=﹣5一定有两个不相等的实数根.
20.如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,求该长方体的底面宽,若该长方体的底面宽为x米:
(1)用含x的代数式分别表示出该长方体的底面长和容积.
(2)请列出关于x的方程.
【答案】见试题解答内容
【解答】解:(1)长方体运输箱底面的宽为xm,则长为(x+2)m.
容积为x(x+2)×1=x2+2x;
(2)x2+2x=15.
21.先阅读材料,然后按照要求答题.
阅读材料:为了解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,(x2﹣1)2=y2,则原方程可化为:y2﹣5y+4=0①
解得:y1=1,y2=4
当y=1时,x2﹣1=1,x2=2,
∴x=±,
当y=4时,x2﹣1=4,x2=5,
∴x=±,
∴原方程的解为:x1=,x2=﹣,x3=,x4=﹣,
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用 换元 法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决问题:若(m2+n2﹣2)(m2+n2)=8,求m2+n2的值.
【答案】(1)换元;
(2)4.
【解答】解:(1)上述解题过程,在由原方程得到方程①的过程中,利用换元法达到了解方程的目的,体现了转化的数学思想,
故答案为:换元;
(2)(m2+n2﹣2)(m2+n2)=8,
设m2+n2=x,
则原方程化为:(x﹣2)x=8,
即x2﹣2x﹣8=0,
解得:x=4或﹣2,
当x=4时,m2+n2=4,
当x=﹣2时,m2+n2=﹣1,
因为不论m、n为何值,m2+n2≥0,
所以m2+n2=﹣2不符合,舍去,
即m2+n2=4.
22.我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用,例如:试求二次三项式x2+4x+5最小值.解:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1,即x2+4x+5的最小值是1.试利用“配方法”解决下列问题:
(1)已知y=x2﹣6x+12,求y的最小值.
(2)比较代数式3x2﹣x+2与2x2+3x﹣6的大小,并说明理由.
知识迁移:
(3)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P在AC边上以2cm/s的速度从点A向C移动,点Q在CB边上以1cm/s的速度从点C向点B移动.若点P,Q同时出发,且当一点移动到终点时,另一点也随之停止,设四边形APQB的面积为Scm2,运动时间为t秒,求S的最小值.
【答案】(1)3;
(2)3x2﹣x+2>2x2+3x﹣6;
(3)5.
【解答】解:(1)∵y=x2﹣6x+12,
∴y=(x﹣3)2+3,
∴y的最小值为3;
(2)3x2﹣x+2﹣(2x2+3x﹣6)
=3x2﹣x+2﹣2x2﹣3x+6
=x2﹣4x+8
=(x﹣2)2+4
∵(x﹣2)2+4>0
∴3x2﹣x+2>2x2+3x﹣6;
(3)根据题意可得:
S=S△ABC﹣S△PQC,
S=×4×3﹣(4﹣2t)t,
S=6﹣2t+t2,
S=(t﹣1)2+5,
∴S的最小值为5.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
