第12章一次函数 单元复习题2022-2023学年沪科版八年级数学上册(含解析)
文档属性
| 名称 | 第12章一次函数 单元复习题2022-2023学年沪科版八年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 263.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 19:13:04 | ||
图片预览



文档简介
沪科版八年级数学上册第12章一次函数 单元复习题
一、选择题
1.某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,( )
A.s是变量 B.t是常量 C.v是常量 D.s是常量
2.函数y=x-1的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
3.已知直线y= -3x-4与直线y=kx+2平行,则k的值为( ).
A.-3 B.3 C.-4 D.4
4.如图所示图象中,表示y是x的函数的有( )
A.1个 B.2个 C.3个 D.4个
5.一列火车由甲市驶往相距的乙市,火车的速度是时,火车离乙市的距离单位:随行驶时间单位:小时 变化的关系用图表示正确的是( )
A. B. C. D.
6.一次函数y=x+2的图象与y轴的交点坐标为( )
A.(0,2) B.(0,-2) C.(2,0) D.(-2,0)
7.直线与在同一平面直角坐标系内,其位置可能是( )
A. B. C. D.
8.已知(m,n是不为0的常数),则下列描述正确的是( )
A.若,则当x的值增大时,y的值也随之增大
B.若,则当x的值增大时,y的值也随之增头
C.若m,n同号,则当x的值增大时,y的值也随之增大
D.若m,n异号,则当x的值增大时,y的值也随之增大
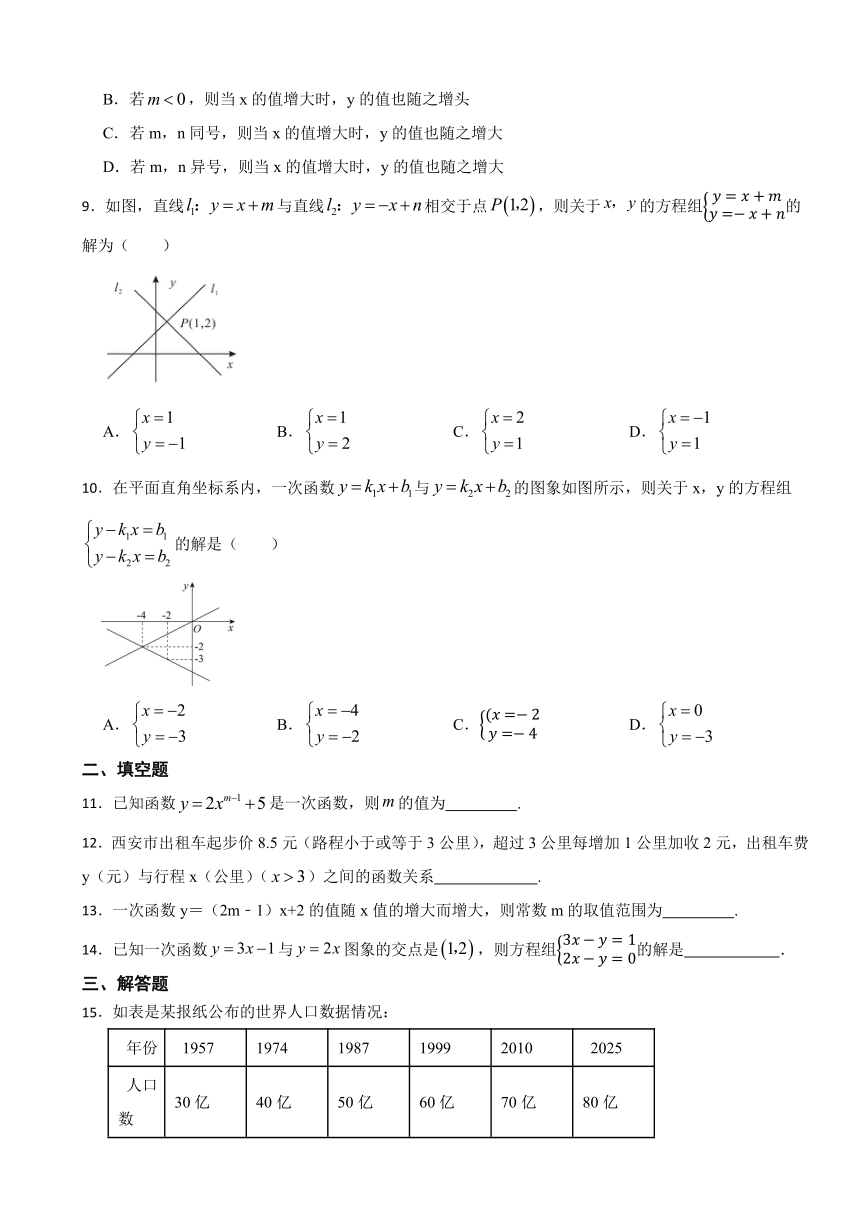
9.如图,直线与直线相交于点,则关于的方程组的解为( )
A. B. C. D.
10.在平面直角坐标系内,一次函数与的图象如图所示,则关于x,y的方程组的解是( )
A. B. C. D.
二、填空题
11.已知函数是一次函数,则的值为 .
12.西安市出租车起步价8.5元(路程小于或等于3公里),超过3公里每增加1公里加收2元,出租车费y(元)与行程x(公里)()之间的函数关系 .
13.一次函数y=(2m﹣1)x+2的值随x值的增大而增大,则常数m的取值范围为 .
14.已知一次函数与图象的交点是,则方程组的解是 .
三、解答题
15.如表是某报纸公布的世界人口数据情况:
年份 1957 1974 1987 1999 2010 2025
人口数 30亿 40亿 50亿 60亿 70亿 80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
16.已知一次函数y=ax-3,当x=1时,y=7,当x=-2时,求y的值.
17.设一次函数y=kx+b的图象过点A(2,﹣1)和点B,其中点B是直线y= x+3与y轴的交点,求这个一次函数的解析式.
四、综合题
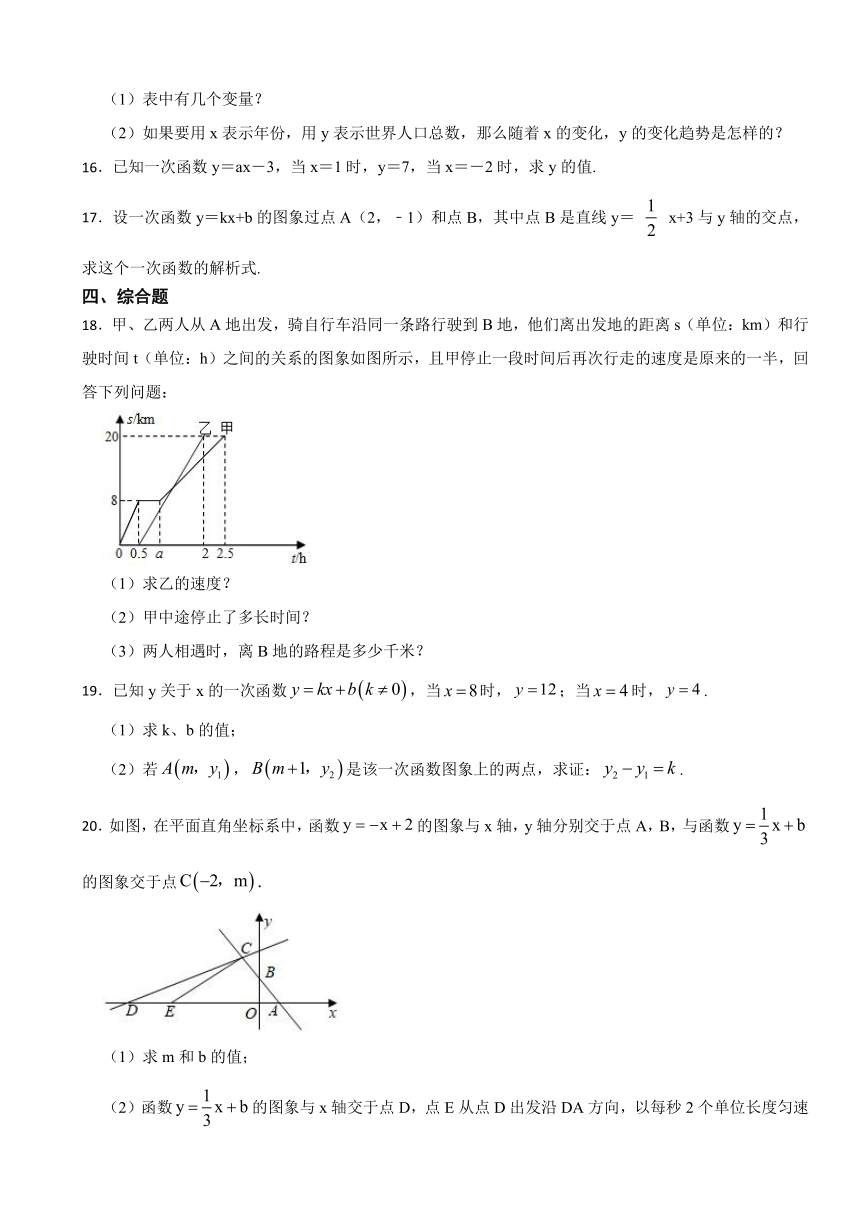
18.甲、乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图象如图所示,且甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
(1)求乙的速度?
(2)甲中途停止了多长时间?
(3)两人相遇时,离B地的路程是多少千米?
19.已知y关于x的一次函数,当时,;当时,.
(1)求k、b的值;
(2)若,是该一次函数图象上的两点,求证:.
20.如图,在平面直角坐标系中,函数的图象与x轴,y轴分别交于点A,B,与函数的图象交于点.
(1)求m和b的值;
(2)函数的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速向x轴正方向运动.设点E的运动时间为t秒.当的面积为12时,求t的值;
答案解析部分
1.【答案】D
【解析】【解答】解:某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,v和t是变量,s是常量.
故答案为:D
【分析】由题意可知速度随着时间的变化而变化,路程不变,可得到此变化过程中的常量.
2.【答案】D
【解析】【解答】解:∵一次函数的一次项系数为,常数项为,
∴此函数的图象经过第一、三、四象限,
故答案为:D.
【分析】一次函数y=kx+b(k≠0),当k>0,b>0时, 一次函数图象经过第一、二、三象限;当k>0,b<0时, 一次函数图象经过第一、三、四象限;当k<0,b>0时, 一次函数图象经过第一、二、四象限;当k<0,b<0时, 一次函数图象经过第二、三、四象限,据此判断即可.
3.【答案】A
【解析】【解答】解:若直线 和直线 平行,则 ,
∵直线 与直线 平行,
∴
故答案为:A.
【分析】根据"两直线平行,k值相等"可求解.
4.【答案】B
【解析】【解答】解:根据每个自变量都只能对应唯一函数值判断,第一幅图和第二幅图符合函数概念的要求。
故答案为B。
【分析】根据函数的概念,对于自变量x的每一个值,因变量y都有唯一的值与它对应解答即可。
5.【答案】D
【解析】【解答】解:由题意得:s与t的函数关系式为,其中,
所以函数图象是D.
故答案为:D.
【分析】根据火车距离乙市的距离等于两地之间的距离减去火车形式的路程,求出s与t的函数关系式及自变量的取值范围,再判断即可.
6.【答案】A
【解析】【解答】当x=0时,y=2。故一次函数图象与y轴的交点坐标为:(0,2)。
故答案为:A。
【分析】图像与y轴交点横坐标为0,代入x值即可求出y值,即可写出与y轴交点坐标。
7.【答案】B
【解析】【解答】解:因为时,的直线过第一、三、四象限,可以排除C、D选项;
当时,经过第一,二,四象限,的图象经过第一,三,四象限,只有选项B正确,
故答案为:B.
【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限.
8.【答案】D
【解析】【解答】解:∵
∴
∴m,n异号时,>0,y随x增大而增大,
m,n同号时,<0,y随x增大而减小,
故答案为:D.
【分析】根据已知条件可得y=x+,当m、n异号时,>0;当m、n同号时,<0,然后结合一次函数的性质进行判断.
9.【答案】B
【解析】【解答】解:∵直线与直线相交于点,
∴关于的方程组的解为.
故答案为:B.
【分析】根据两一次函数图象的交点坐标即为对应的二元一次方程组的解进行解答.
10.【答案】B
【解析】【解答】解:∵一次函数y=k1x+b1与y=k2x+b2交于点A(-4,-2),
∴方程组的解是,
故答案为:B.
【分析】根据一次函数与二元一次方程组的关系可知:两函数图象的交点坐标即是方程组的解,从而得解。
11.【答案】2
【解析】【解答】解:依题意,,
解得:,
故答案为:2.
【分析】一次函数的一般形式为y=kx+b(k≠0),则m-1=1,求解可得m的值.
12.【答案】
【解析】【解答】解:设乘出租车,应付y元车费.
∵每增加1公里加收2元,
∴根据题意得:当时,.
故答案为:.
【分析】设乘出租车xkm,应付y元车费,当x>3时,超过3公里的费用为2(x-3),加上起步价可得y与x的关系式.
13.【答案】m>
【解析】【解答】解:∵一次函数y=(2m﹣1)x+2中,函数值y随自变量x的增大而增大,
∴2m﹣1>0,解得m> .
故答案为:m> .
【分析】根据一次函数的性质结合题意可得2m-1>0,求解可得m的范围.
14.【答案】
【解析】【解答】解:∵一次函数与的图象的交点是,
∴方程组的解为.
故答案为:.
【分析】根据一次函数与二元一次方程组的关系:两函数图象的交点坐标即是方程组的解求解即可。
15.【答案】解:(1)表中有两个变量,分别是年份和人口数;
(2)用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是增大.
【解析】【分析】(1)年份和人口数都在变化,据此得到;
(2)根据人口的变化写出变化趋势即可;
16.【答案】解:根据题意得: ,
∴ ,
∴一次函数解析式为 ,
∴当x=-2时,y=10 (-2)-3=-23 ,
∴y 的值为-23.
【解析】【分析】将x=1、y=7代入可得a-3=7,求出a的值,据此可得一次函数的解析式,然后将x=-2代入求解就可得到y的值.
17.【答案】解:当x=0时,y= x+3=3,则B点坐标为(0,3),
把A(2,﹣1),B(0,3)代入y=kx+b得 ,
解得 ,
所以一次函数解析式为y=﹣2x+3.
【解析】【分析】根据直线y=x+3与y轴相交可令x=0求得x的值,则点B的坐标可求解;然后用待定系数法可求得直线AB的解析式.
18.【答案】(1)解:乙的速度为,
答:乙的速度为.
(2)解:甲停止前的速度为,
甲停止一段时间后再次行走的速度为,
则,
所以甲中途停止的时间为,
答:甲中途停止了.
(3)解:设乙骑行了小时与甲相遇,
因为,
所以,
则可列方程为,
解得,
则,
答:两人相遇时,离B地的路程是10千米.
【解析】【分析】(1)由图象可知乙1.5小时行走20千米,根据速度=路程÷速度即可求出乙的速度;
(2)先由甲0.5小时行走8千米求出甲原来的速度,即可求出甲停止一段时间后再次行走的速度,由甲甲停止一段时间后再次用(2.5-a)小时行走(20-8)千米,根据路程÷时间=速度建立方程可求出a值,继而求解;
(3)设乙骑行了小时与甲相遇,根据甲、乙相遇时所走的路程相等列出方程并解之,继而得解.
19.【答案】(1)解:把,;,代入,得
,解得
(2)证明:由(1)可知:函数解析式为,
把,代入解析式得:
,,
∴
【解析】【分析】(1)将x=8、y=12;x=4、y=4代入y=kx+b中进行计算可得k、b的值;
(2)根据k、b的值可得函数解析式,将A(m,y1)、B(m+1,y2)代入可得y1、y2,然后作差即可.
20.【答案】(1)解:∵点C( 2,m)在直线y= x+2上,
∴m= ( 2)+2=2+2=4,
∴点C( 2,4),
∵函数y=x+b的图象过点C( 2,4),
∴4=×( 2)+b,解得b=,
即m的值是4,b的值是;
(2)(2)∵函数y= x+2的图象与x轴,y轴分别交于点A,B,
∴点A(2,0),点B(0,2),
∵函数y=x+的图象与x轴交于点D,
∴点D的坐标为( 14,0),
∴AD=16,
由题意可得,DE=2t,
当点E在线段AD上时,AE=16 2t,
由(1)知点C的坐标为( 2,4),
∵△ACE的面积为12,
∴,
解得,t=5,
当点E在线段DA的延长线上时,AE=2t-16,
∵△ACE的面积为12,
∴,
解得,t=11,
即当△ACE的面积为12时,t的值是5或11.
【解析】【分析】(1)将点C( 2,m)代入y= x+2,可以求得m的值,从而可以得到点C的坐标,再将点C的坐标代入y=x+b,可以得到b的值;
(2)分别令求y= x+2中的x=0与y=0算出对应的y与x的值,得点A、点B的坐标,令y=x+中的y=0算出对应的x的值可得点D的坐标,然后分当点E在线段AD上时与当点E在线段DA的延长线上时两种情况,用含t的代数式表示出AE的长度,然后根据△ACE的面积为12,建立方程即可得到t的值.
一、选择题
1.某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,( )
A.s是变量 B.t是常量 C.v是常量 D.s是常量
2.函数y=x-1的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
3.已知直线y= -3x-4与直线y=kx+2平行,则k的值为( ).
A.-3 B.3 C.-4 D.4
4.如图所示图象中,表示y是x的函数的有( )
A.1个 B.2个 C.3个 D.4个
5.一列火车由甲市驶往相距的乙市,火车的速度是时,火车离乙市的距离单位:随行驶时间单位:小时 变化的关系用图表示正确的是( )
A. B. C. D.
6.一次函数y=x+2的图象与y轴的交点坐标为( )
A.(0,2) B.(0,-2) C.(2,0) D.(-2,0)
7.直线与在同一平面直角坐标系内,其位置可能是( )
A. B. C. D.
8.已知(m,n是不为0的常数),则下列描述正确的是( )
A.若,则当x的值增大时,y的值也随之增大
B.若,则当x的值增大时,y的值也随之增头
C.若m,n同号,则当x的值增大时,y的值也随之增大
D.若m,n异号,则当x的值增大时,y的值也随之增大
9.如图,直线与直线相交于点,则关于的方程组的解为( )
A. B. C. D.
10.在平面直角坐标系内,一次函数与的图象如图所示,则关于x,y的方程组的解是( )
A. B. C. D.
二、填空题
11.已知函数是一次函数,则的值为 .
12.西安市出租车起步价8.5元(路程小于或等于3公里),超过3公里每增加1公里加收2元,出租车费y(元)与行程x(公里)()之间的函数关系 .
13.一次函数y=(2m﹣1)x+2的值随x值的增大而增大,则常数m的取值范围为 .
14.已知一次函数与图象的交点是,则方程组的解是 .
三、解答题
15.如表是某报纸公布的世界人口数据情况:
年份 1957 1974 1987 1999 2010 2025
人口数 30亿 40亿 50亿 60亿 70亿 80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
16.已知一次函数y=ax-3,当x=1时,y=7,当x=-2时,求y的值.
17.设一次函数y=kx+b的图象过点A(2,﹣1)和点B,其中点B是直线y= x+3与y轴的交点,求这个一次函数的解析式.
四、综合题
18.甲、乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图象如图所示,且甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
(1)求乙的速度?
(2)甲中途停止了多长时间?
(3)两人相遇时,离B地的路程是多少千米?
19.已知y关于x的一次函数,当时,;当时,.
(1)求k、b的值;
(2)若,是该一次函数图象上的两点,求证:.
20.如图,在平面直角坐标系中,函数的图象与x轴,y轴分别交于点A,B,与函数的图象交于点.
(1)求m和b的值;
(2)函数的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速向x轴正方向运动.设点E的运动时间为t秒.当的面积为12时,求t的值;
答案解析部分
1.【答案】D
【解析】【解答】解:某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,v和t是变量,s是常量.
故答案为:D
【分析】由题意可知速度随着时间的变化而变化,路程不变,可得到此变化过程中的常量.
2.【答案】D
【解析】【解答】解:∵一次函数的一次项系数为,常数项为,
∴此函数的图象经过第一、三、四象限,
故答案为:D.
【分析】一次函数y=kx+b(k≠0),当k>0,b>0时, 一次函数图象经过第一、二、三象限;当k>0,b<0时, 一次函数图象经过第一、三、四象限;当k<0,b>0时, 一次函数图象经过第一、二、四象限;当k<0,b<0时, 一次函数图象经过第二、三、四象限,据此判断即可.
3.【答案】A
【解析】【解答】解:若直线 和直线 平行,则 ,
∵直线 与直线 平行,
∴
故答案为:A.
【分析】根据"两直线平行,k值相等"可求解.
4.【答案】B
【解析】【解答】解:根据每个自变量都只能对应唯一函数值判断,第一幅图和第二幅图符合函数概念的要求。
故答案为B。
【分析】根据函数的概念,对于自变量x的每一个值,因变量y都有唯一的值与它对应解答即可。
5.【答案】D
【解析】【解答】解:由题意得:s与t的函数关系式为,其中,
所以函数图象是D.
故答案为:D.
【分析】根据火车距离乙市的距离等于两地之间的距离减去火车形式的路程,求出s与t的函数关系式及自变量的取值范围,再判断即可.
6.【答案】A
【解析】【解答】当x=0时,y=2。故一次函数图象与y轴的交点坐标为:(0,2)。
故答案为:A。
【分析】图像与y轴交点横坐标为0,代入x值即可求出y值,即可写出与y轴交点坐标。
7.【答案】B
【解析】【解答】解:因为时,的直线过第一、三、四象限,可以排除C、D选项;
当时,经过第一,二,四象限,的图象经过第一,三,四象限,只有选项B正确,
故答案为:B.
【分析】y=ax+b(a≠0),当a>0,b>0时,图象过一、二、三象;当a>0,b<0时,图象过一、三、四象限;当a<0,b>0时,图象过一、二、四象限;当a<0,b<0时,图象过二、三、四象限.
8.【答案】D
【解析】【解答】解:∵
∴
∴m,n异号时,>0,y随x增大而增大,
m,n同号时,<0,y随x增大而减小,
故答案为:D.
【分析】根据已知条件可得y=x+,当m、n异号时,>0;当m、n同号时,<0,然后结合一次函数的性质进行判断.
9.【答案】B
【解析】【解答】解:∵直线与直线相交于点,
∴关于的方程组的解为.
故答案为:B.
【分析】根据两一次函数图象的交点坐标即为对应的二元一次方程组的解进行解答.
10.【答案】B
【解析】【解答】解:∵一次函数y=k1x+b1与y=k2x+b2交于点A(-4,-2),
∴方程组的解是,
故答案为:B.
【分析】根据一次函数与二元一次方程组的关系可知:两函数图象的交点坐标即是方程组的解,从而得解。
11.【答案】2
【解析】【解答】解:依题意,,
解得:,
故答案为:2.
【分析】一次函数的一般形式为y=kx+b(k≠0),则m-1=1,求解可得m的值.
12.【答案】
【解析】【解答】解:设乘出租车,应付y元车费.
∵每增加1公里加收2元,
∴根据题意得:当时,.
故答案为:.
【分析】设乘出租车xkm,应付y元车费,当x>3时,超过3公里的费用为2(x-3),加上起步价可得y与x的关系式.
13.【答案】m>
【解析】【解答】解:∵一次函数y=(2m﹣1)x+2中,函数值y随自变量x的增大而增大,
∴2m﹣1>0,解得m> .
故答案为:m> .
【分析】根据一次函数的性质结合题意可得2m-1>0,求解可得m的范围.
14.【答案】
【解析】【解答】解:∵一次函数与的图象的交点是,
∴方程组的解为.
故答案为:.
【分析】根据一次函数与二元一次方程组的关系:两函数图象的交点坐标即是方程组的解求解即可。
15.【答案】解:(1)表中有两个变量,分别是年份和人口数;
(2)用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是增大.
【解析】【分析】(1)年份和人口数都在变化,据此得到;
(2)根据人口的变化写出变化趋势即可;
16.【答案】解:根据题意得: ,
∴ ,
∴一次函数解析式为 ,
∴当x=-2时,y=10 (-2)-3=-23 ,
∴y 的值为-23.
【解析】【分析】将x=1、y=7代入可得a-3=7,求出a的值,据此可得一次函数的解析式,然后将x=-2代入求解就可得到y的值.
17.【答案】解:当x=0时,y= x+3=3,则B点坐标为(0,3),
把A(2,﹣1),B(0,3)代入y=kx+b得 ,
解得 ,
所以一次函数解析式为y=﹣2x+3.
【解析】【分析】根据直线y=x+3与y轴相交可令x=0求得x的值,则点B的坐标可求解;然后用待定系数法可求得直线AB的解析式.
18.【答案】(1)解:乙的速度为,
答:乙的速度为.
(2)解:甲停止前的速度为,
甲停止一段时间后再次行走的速度为,
则,
所以甲中途停止的时间为,
答:甲中途停止了.
(3)解:设乙骑行了小时与甲相遇,
因为,
所以,
则可列方程为,
解得,
则,
答:两人相遇时,离B地的路程是10千米.
【解析】【分析】(1)由图象可知乙1.5小时行走20千米,根据速度=路程÷速度即可求出乙的速度;
(2)先由甲0.5小时行走8千米求出甲原来的速度,即可求出甲停止一段时间后再次行走的速度,由甲甲停止一段时间后再次用(2.5-a)小时行走(20-8)千米,根据路程÷时间=速度建立方程可求出a值,继而求解;
(3)设乙骑行了小时与甲相遇,根据甲、乙相遇时所走的路程相等列出方程并解之,继而得解.
19.【答案】(1)解:把,;,代入,得
,解得
(2)证明:由(1)可知:函数解析式为,
把,代入解析式得:
,,
∴
【解析】【分析】(1)将x=8、y=12;x=4、y=4代入y=kx+b中进行计算可得k、b的值;
(2)根据k、b的值可得函数解析式,将A(m,y1)、B(m+1,y2)代入可得y1、y2,然后作差即可.
20.【答案】(1)解:∵点C( 2,m)在直线y= x+2上,
∴m= ( 2)+2=2+2=4,
∴点C( 2,4),
∵函数y=x+b的图象过点C( 2,4),
∴4=×( 2)+b,解得b=,
即m的值是4,b的值是;
(2)(2)∵函数y= x+2的图象与x轴,y轴分别交于点A,B,
∴点A(2,0),点B(0,2),
∵函数y=x+的图象与x轴交于点D,
∴点D的坐标为( 14,0),
∴AD=16,
由题意可得,DE=2t,
当点E在线段AD上时,AE=16 2t,
由(1)知点C的坐标为( 2,4),
∵△ACE的面积为12,
∴,
解得,t=5,
当点E在线段DA的延长线上时,AE=2t-16,
∵△ACE的面积为12,
∴,
解得,t=11,
即当△ACE的面积为12时,t的值是5或11.
【解析】【分析】(1)将点C( 2,m)代入y= x+2,可以求得m的值,从而可以得到点C的坐标,再将点C的坐标代入y=x+b,可以得到b的值;
(2)分别令求y= x+2中的x=0与y=0算出对应的y与x的值,得点A、点B的坐标,令y=x+中的y=0算出对应的x的值可得点D的坐标,然后分当点E在线段AD上时与当点E在线段DA的延长线上时两种情况,用含t的代数式表示出AE的长度,然后根据△ACE的面积为12,建立方程即可得到t的值.
