直线和双曲线的关系
图片预览




文档简介
课件15张PPT。直线与抛物线一、直线与抛物线位置关系种类1、相离;2、相切;3、相交(一个交点,两个交点)1、相离;2、相切;3、相交(一个交点,两个交点)与双曲线的情况一样二、判断方法探讨1、直线与抛物线的对称轴平行例:计算直线 y = 6
与抛物线 y2 =4x 的位置关系计算结果:得到一元一次方程,容易解出交点坐标xyO二、判断方法探讨2、直线与抛物线的对称轴不平行例:计算直线 y = x -1与
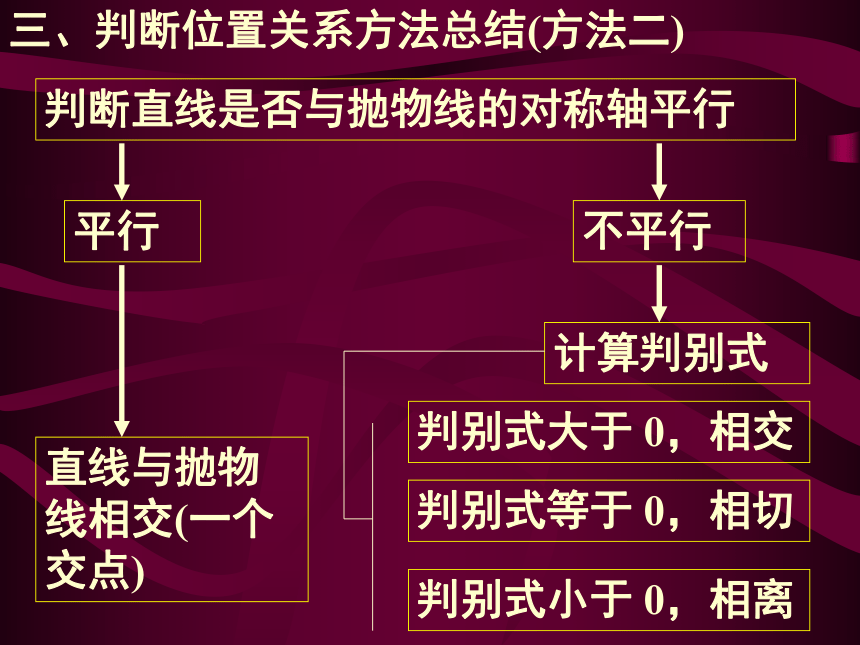
抛物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相交。三、判断位置关系方法总结(方法一)把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交(一个交点)计算判别式判别式大于 0,相交判别式等于 0,相切判别式小于 0,相离三、判断位置关系方法总结(方法二)判断直线是否与抛物线的对称轴平行不平行直线与抛物线相交(一个交点)计算判别式判别式大于 0,相交判别式等于 0,相切判别式小于 0,相离平行四、直线与圆锥曲线位置关系判断方法的回顾直线与圆把直线方程代入圆的方程得到一元 二次方程计 算 判 别 式? > 0, 相 交? = 0, 相 切? < 0, 相 离[1]判断直线与椭圆位置关系的根本方法是解直线方程和椭圆方程组成的方程组[2]把直线方程代入椭圆方程后,若一元二次方程好解,则应解方程;若一元二次方程不好解,则计算判别式。 把直线方程代入 椭圆方程得到一元二次方程方程好解方程不好解计算判别式解方程 交 点 个 数 位 置 关 系判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式直线与抛物线把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交(一个交点)计算判别式判别式大于 0,相交判别式等于 0,相切判别式小于 0,相离判断直线与曲线位置关系的操作程序把直线方程代入曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐进线
或抛物线的对称轴平行相交(一个交点) 计 算 判 别 式练习:教材:101页 5过抛物线 y2=2x的焦点做倾斜角为450的弦AB,则AB的长度是多少?答: 4作业101页 7,8,9
与抛物线 y2 =4x 的位置关系计算结果:得到一元一次方程,容易解出交点坐标xyO二、判断方法探讨2、直线与抛物线的对称轴不平行例:计算直线 y = x -1与
抛物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相交。三、判断位置关系方法总结(方法一)把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交(一个交点)计算判别式判别式大于 0,相交判别式等于 0,相切判别式小于 0,相离三、判断位置关系方法总结(方法二)判断直线是否与抛物线的对称轴平行不平行直线与抛物线相交(一个交点)计算判别式判别式大于 0,相交判别式等于 0,相切判别式小于 0,相离平行四、直线与圆锥曲线位置关系判断方法的回顾直线与圆把直线方程代入圆的方程得到一元 二次方程计 算 判 别 式? > 0, 相 交? = 0, 相 切? < 0, 相 离[1]判断直线与椭圆位置关系的根本方法是解直线方程和椭圆方程组成的方程组[2]把直线方程代入椭圆方程后,若一元二次方程好解,则应解方程;若一元二次方程不好解,则计算判别式。 把直线方程代入 椭圆方程得到一元二次方程方程好解方程不好解计算判别式解方程 交 点 个 数 位 置 关 系判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式直线与抛物线把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交(一个交点)计算判别式判别式大于 0,相交判别式等于 0,相切判别式小于 0,相离判断直线与曲线位置关系的操作程序把直线方程代入曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐进线
或抛物线的对称轴平行相交(一个交点) 计 算 判 别 式练习:教材:101页 5过抛物线 y2=2x的焦点做倾斜角为450的弦AB,则AB的长度是多少?答: 4作业101页 7,8,9
