相似三角形判定
图片预览



文档简介
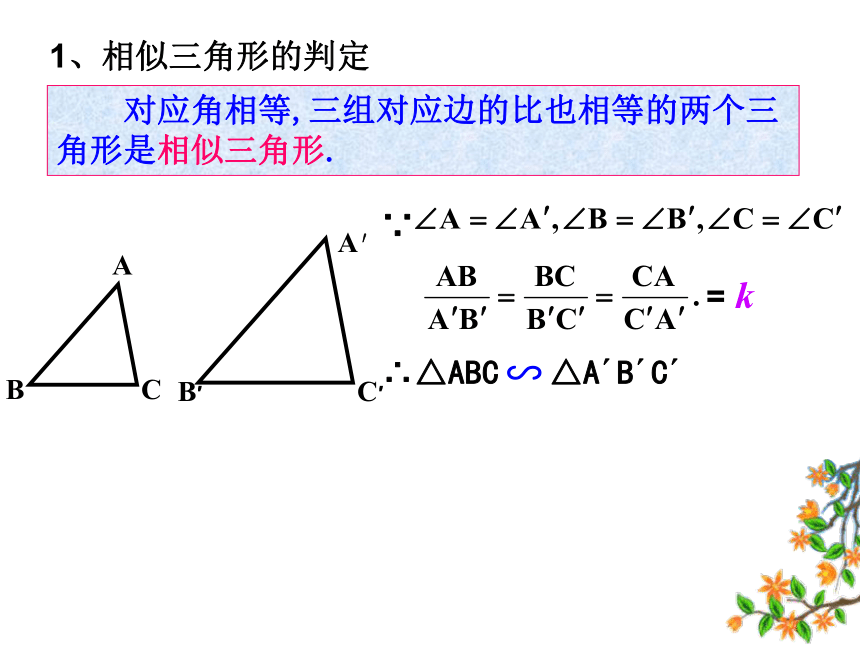
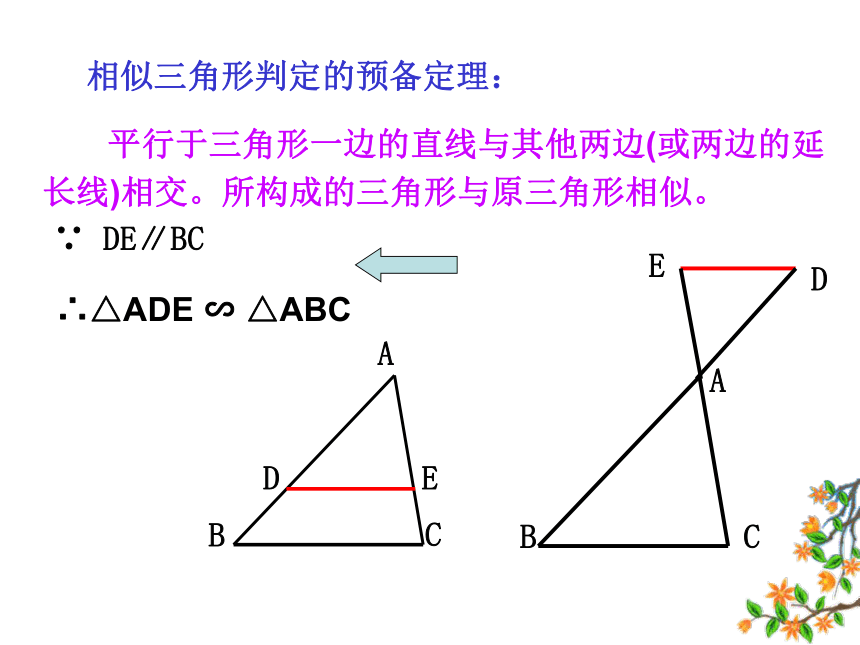
课件19张PPT。27.2.1 相似三角形的判定(一) 对应角相等,三组对应边的比也相等的两个三角形是相似三角形.1、相似三角形的判定= k∴△ABC △A′B′C′∵∽∵ DE∥BC∴△ADE ∽ △ABC 平行于三角形一边的直线与其他两边(或两边的延长线)相交。所构成的三角形与原三角形相似。相似三角形判定的预备定理:提出问题1.除了上述的两个三角形相似判定外.还有比其更简洁判定的吗?2.在△ABC和△A′B′C′中
如果满足,
那么能否判定这两个三角形相似?
问题探究请同学们按照下列要求作图
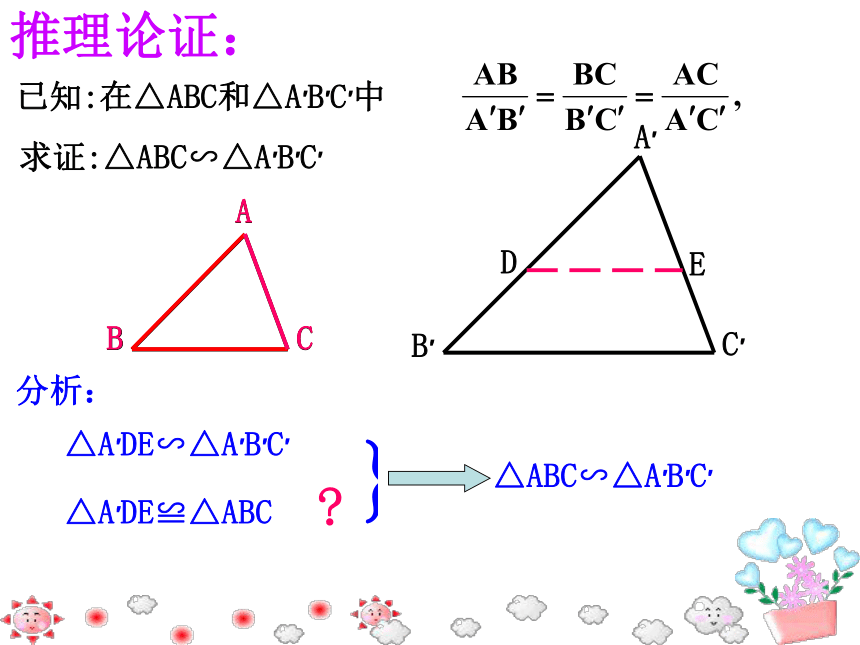
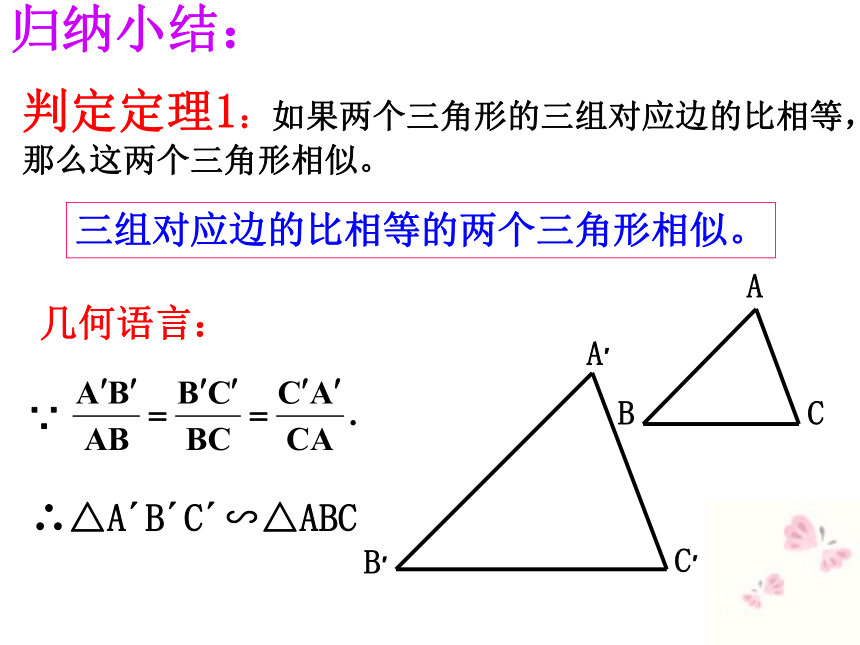
1.任意画△ABC. 2.再画△A′B′C′,使它的各边长都是△ABC的3倍3.把画好的两个三角形剪下.4.比较它们的对应角相等?分组讨论5.能说明三角形△ABC ∽ △ A′B′C′, 分组讨论推理论证:分析:△A′DE≌△ABC?归纳小结:判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:三组对应边的比相等的两个三角形相似。∴△A′B′C′∽△ABC∵牛刀小试: 根据条件判断下列的两个三角形是否相似。(1)如右图(3) △ABC的三边长分别为
△A′B′C′的三边分别为(2)AB=6cm,BC=10cm,AC=8cm;
A1B1=25cm,B1C1=15cm,A1C1=20cm(4)ACBA1B1C1(5)AB=3,BC=4,AC=6; DE=6,EF=9,DF=12例题教学:例1 如图,判断4×4方格中的两个三角形是否相似,并说明理由.例题教学:例2 求证:三角形的三条中位线所组成的三角形 与原三角形相似。已知:求证:如图,DE,DF,EF是△ABC的中位线△ABC∽△FED证明:∵ DE,DF,EF是△ABC的中位线∴ DE= BC,DF= AC,EF= AB∴∴ △ABC∽△DEF例题教学:已知:如图,DE,DF,EF是△ABC的中位线。(1)请找出图中的相似三角形。∽∽∽∽例题教学:证明:即 ∠BAD=∠CAE∵∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC 课堂巩固题1.如图∠B=90°AB=BE=EF=FC=1
求证:(1)
(2) ∠C+ ∠AFE=45°∽AAA例题教学: 例题4,如图在正方形ABCD中,P是
BC边上一点,且 Q是DC的中点.
求证:∠DAQ= ∠CQP
提示设AD=a,
通过计算找三角形相似请你帮忙: 图纸上上有不锈钢三角架的长分别20cm,50cm,60cm,库存的不锈钢条有两根中,一根长30cm,另一根长60cm,工人师傅想用其中一根做三角架的一边,在另一根上取两截,(允许有余料)用来做三角架的另外两边,使做成的三角架与图纸上的形状相同(即图形相似)。请帮他确定:共有几种不同的做法(焊接用料略去不计)?205060相似三角形判定方法1、三组对应边的比相等的两个三角形相似。总结反思 与同桌交流一下你这节课的收获! 2.能通过三角形相似证明角等,即给出了角相等又一个证明方法3.除了上述我们学过的证明三角形相似的判定方法还能有别判定的方法?作业:选做题:《作业本》必做题:《课本》P55 面
第1、3、4、5题合作习题: 为美化校园,学校决定对东教学楼后面的一块三角形的空地(如图)进行修整,现已测量出AB=12m,BC=16m,CA=24m,请你用适当的比例为这块空地画出图纸。1.量一量,与同桌交流一下,你们所画的两个三角形的对应角相等吗?两个三角形各边的对应比相等2.猜测:三组对应边的比相等的两个三角形是否相似?
如果满足,
那么能否判定这两个三角形相似?
问题探究请同学们按照下列要求作图
1.任意画△ABC. 2.再画△A′B′C′,使它的各边长都是△ABC的3倍3.把画好的两个三角形剪下.4.比较它们的对应角相等?分组讨论5.能说明三角形△ABC ∽ △ A′B′C′, 分组讨论推理论证:分析:△A′DE≌△ABC?归纳小结:判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。几何语言:三组对应边的比相等的两个三角形相似。∴△A′B′C′∽△ABC∵牛刀小试: 根据条件判断下列的两个三角形是否相似。(1)如右图(3) △ABC的三边长分别为
△A′B′C′的三边分别为(2)AB=6cm,BC=10cm,AC=8cm;
A1B1=25cm,B1C1=15cm,A1C1=20cm(4)ACBA1B1C1(5)AB=3,BC=4,AC=6; DE=6,EF=9,DF=12例题教学:例1 如图,判断4×4方格中的两个三角形是否相似,并说明理由.例题教学:例2 求证:三角形的三条中位线所组成的三角形 与原三角形相似。已知:求证:如图,DE,DF,EF是△ABC的中位线△ABC∽△FED证明:∵ DE,DF,EF是△ABC的中位线∴ DE= BC,DF= AC,EF= AB∴∴ △ABC∽△DEF例题教学:已知:如图,DE,DF,EF是△ABC的中位线。(1)请找出图中的相似三角形。∽∽∽∽例题教学:证明:即 ∠BAD=∠CAE∵∴△ABC∽△ADE∴∠BAC=∠DAE∴∠BAC-∠DAC =∠DAE-∠DAC 课堂巩固题1.如图∠B=90°AB=BE=EF=FC=1
求证:(1)
(2) ∠C+ ∠AFE=45°∽AAA例题教学: 例题4,如图在正方形ABCD中,P是
BC边上一点,且 Q是DC的中点.
求证:∠DAQ= ∠CQP
提示设AD=a,
通过计算找三角形相似请你帮忙: 图纸上上有不锈钢三角架的长分别20cm,50cm,60cm,库存的不锈钢条有两根中,一根长30cm,另一根长60cm,工人师傅想用其中一根做三角架的一边,在另一根上取两截,(允许有余料)用来做三角架的另外两边,使做成的三角架与图纸上的形状相同(即图形相似)。请帮他确定:共有几种不同的做法(焊接用料略去不计)?205060相似三角形判定方法1、三组对应边的比相等的两个三角形相似。总结反思 与同桌交流一下你这节课的收获! 2.能通过三角形相似证明角等,即给出了角相等又一个证明方法3.除了上述我们学过的证明三角形相似的判定方法还能有别判定的方法?作业:选做题:《作业本》必做题:《课本》P55 面
第1、3、4、5题合作习题: 为美化校园,学校决定对东教学楼后面的一块三角形的空地(如图)进行修整,现已测量出AB=12m,BC=16m,CA=24m,请你用适当的比例为这块空地画出图纸。1.量一量,与同桌交流一下,你们所画的两个三角形的对应角相等吗?两个三角形各边的对应比相等2.猜测:三组对应边的比相等的两个三角形是否相似?
