2.1整式(第二课时) 课件(25张PPT)
文档属性
| 名称 | 2.1整式(第二课时) 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 10:39:45 | ||
图片预览







文档简介
(共25张PPT)
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第二章整式的加减
2.1整式(第二课时)
学习目标
1. 通过具体实例了解单项式、单项式的系数和次数的概念;
2. 能用代数式表示具体情境中的数量关系;
3. 经历单项式概念的形成过程,从中体会抽象的数学思想,提高观察、分析、归纳、概括能力.
复习提问
你发现这些式子有什么共同特点?
观察式子100t,0.8p,mn,a2h,-n,都有哪些特点?
都是数或字母的积,像这样的式子叫做单项式.
探究新知
单项式的定义:表示数或字母的积的式子叫做单项式.
单独一个数或一个字母也是单项式
一、单项式的定义
探究新知
下列式子中哪些是单项式
√
√
√
√
√
√
探究新知
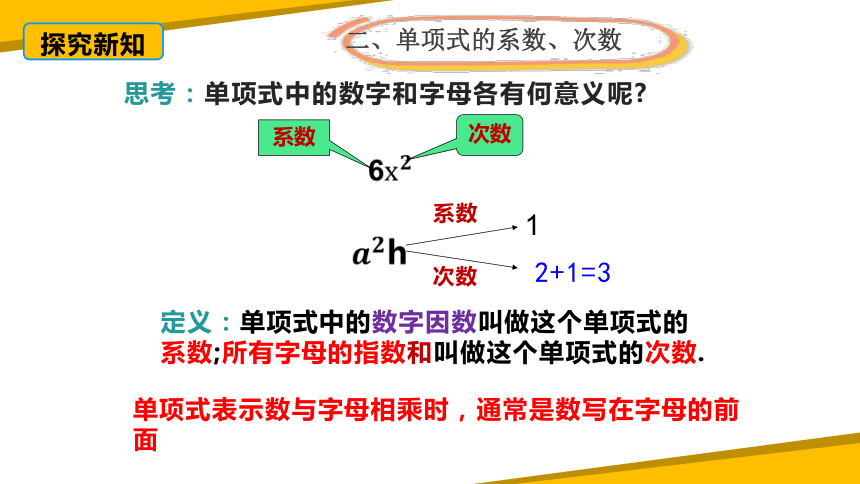
思考:单项式中的数字和字母各有何意义呢
系数
次数
系数
定义:单项式中的数字因数叫做这个单项式的系数;所有字母的指数和叫做这个单项式的次数.
2+1=3
次数
1
二、单项式的系数、次数
单项式表示数与字母相乘时,通常是数写在字母的前面
探究新知
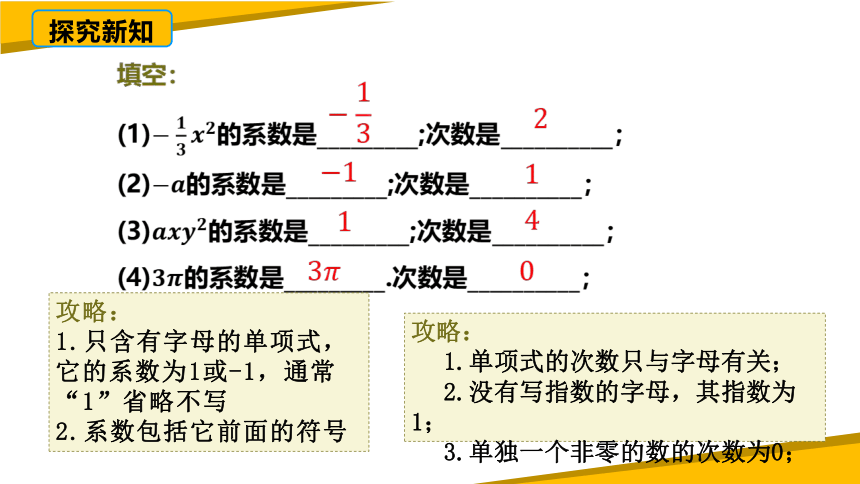
攻略:
1.只含有字母的单项式,它的系数为1或-1,通常“1”省略不写
2.系数包括它前面的符号
攻略:
1.单项式的次数只与字母有关;
2.没有写指数的字母,其指数为1;
3.单独一个非零的数的次数为0;
建立模型
单项式定义:
单独的一个数或一个字母也是单项式.
单项式中的数字因数叫做这个单项式的系数.
如单项式100t,a2h,-n的系数分别是100,1,-1.
单项式的次数:单项式中所有字母的指数的和.
表示数或字母的积的式子
叫做单项式.
单项式的系数:
典例解析
(1) 每包书有12册,n包书有______册;
例1:用单项式填空,并指出它们的系数和次数:
(1)12n,它的系数是12,次数是1;
(2) 底边长为 a cm,高为 h cm的三角形的面积是_____cm2;
(2) ,它的系数是 ,次数是2;
(3)棱长为 a cm的正方体的体积是______cm3 ;
(3)a3,它的系数是1,次数是3;
12n
a3
典例解析
(4)0.9b,它的系数是0.9,次数是1;
(5)0.9b,它的系数是0.9,次数是1.
(4)一台电视机原价 b 元,现按原价的9折出售,这台电视机现在的售价是______元;
(5)一个长方形的长是0.9 m,宽是b m ,这个长方形的面积是______m2.
0.9b
0.9b
例1: 用单项式填空,并指出它们的系数和次数:
典例解析
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1”通常省略不写;
③省略1的字母指数别漏掉;
④单项式次数只与字母指数有关,单独一个非0数字的次数是0.
典例解析
用字母表示数后,同一个式子可以表示不同的含义.
例如,在例题的第(4)(5)小题中 0.9b 既可以表示电视机的售价,又可以表示长方形的面积.
你能赋予 0.9b 一个新的含义吗?
典例解析
你能写出一个只含有x、y,而且系数是-3,次数是4的单项式吗?
-3xy3
-3x2y2
-3x3y
x、y的指数之和为4即可
典例解析
例2:若 是关于 x,y 的一个五次单项式,m,n应满足的条件?
该单项式次数是2+n
所以m≠ 2,n=3.
2+n=5,
m-2 ≠ 0,
为什么m-2 ≠ 0?
解:由题意知m,n要满足
系数为m-2,m当作已知常数看待
针对训练
若-3xa+1y是一个六次单项式,你能说出指数a是几吗?
解:a+1+1=6,a=4
随堂练习
随堂练习
中考链接
课堂小结
次数:所有字母的指数的和.
概念:数与字母的乘积.
系数:单项式中的数字因数.
二、几点注意:
①单独的一个数或一个字母也是单项式;
②当一个单项式的系数是1或-1时,通常省略不写,如x2,-a2b等;
③圆周率π是常数,把它当作系数;
④如果单项式系数为0,它就是0次单项式;
⑤单项式次数只与字母指数有关.
一、单项式的有关概念:
当堂测试
当堂测试
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第二章整式的加减
2.1整式(第二课时)
学习目标
1. 通过具体实例了解单项式、单项式的系数和次数的概念;
2. 能用代数式表示具体情境中的数量关系;
3. 经历单项式概念的形成过程,从中体会抽象的数学思想,提高观察、分析、归纳、概括能力.
复习提问
你发现这些式子有什么共同特点?
观察式子100t,0.8p,mn,a2h,-n,都有哪些特点?
都是数或字母的积,像这样的式子叫做单项式.
探究新知
单项式的定义:表示数或字母的积的式子叫做单项式.
单独一个数或一个字母也是单项式
一、单项式的定义
探究新知
下列式子中哪些是单项式
√
√
√
√
√
√
探究新知
思考:单项式中的数字和字母各有何意义呢
系数
次数
系数
定义:单项式中的数字因数叫做这个单项式的系数;所有字母的指数和叫做这个单项式的次数.
2+1=3
次数
1
二、单项式的系数、次数
单项式表示数与字母相乘时,通常是数写在字母的前面
探究新知
攻略:
1.只含有字母的单项式,它的系数为1或-1,通常“1”省略不写
2.系数包括它前面的符号
攻略:
1.单项式的次数只与字母有关;
2.没有写指数的字母,其指数为1;
3.单独一个非零的数的次数为0;
建立模型
单项式定义:
单独的一个数或一个字母也是单项式.
单项式中的数字因数叫做这个单项式的系数.
如单项式100t,a2h,-n的系数分别是100,1,-1.
单项式的次数:单项式中所有字母的指数的和.
表示数或字母的积的式子
叫做单项式.
单项式的系数:
典例解析
(1) 每包书有12册,n包书有______册;
例1:用单项式填空,并指出它们的系数和次数:
(1)12n,它的系数是12,次数是1;
(2) 底边长为 a cm,高为 h cm的三角形的面积是_____cm2;
(2) ,它的系数是 ,次数是2;
(3)棱长为 a cm的正方体的体积是______cm3 ;
(3)a3,它的系数是1,次数是3;
12n
a3
典例解析
(4)0.9b,它的系数是0.9,次数是1;
(5)0.9b,它的系数是0.9,次数是1.
(4)一台电视机原价 b 元,现按原价的9折出售,这台电视机现在的售价是______元;
(5)一个长方形的长是0.9 m,宽是b m ,这个长方形的面积是______m2.
0.9b
0.9b
例1: 用单项式填空,并指出它们的系数和次数:
典例解析
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②当一个单项式的系数是1或-1时,“1”通常省略不写;
③省略1的字母指数别漏掉;
④单项式次数只与字母指数有关,单独一个非0数字的次数是0.
典例解析
用字母表示数后,同一个式子可以表示不同的含义.
例如,在例题的第(4)(5)小题中 0.9b 既可以表示电视机的售价,又可以表示长方形的面积.
你能赋予 0.9b 一个新的含义吗?
典例解析
你能写出一个只含有x、y,而且系数是-3,次数是4的单项式吗?
-3xy3
-3x2y2
-3x3y
x、y的指数之和为4即可
典例解析
例2:若 是关于 x,y 的一个五次单项式,m,n应满足的条件?
该单项式次数是2+n
所以m≠ 2,n=3.
2+n=5,
m-2 ≠ 0,
为什么m-2 ≠ 0?
解:由题意知m,n要满足
系数为m-2,m当作已知常数看待
针对训练
若-3xa+1y是一个六次单项式,你能说出指数a是几吗?
解:a+1+1=6,a=4
随堂练习
随堂练习
中考链接
课堂小结
次数:所有字母的指数的和.
概念:数与字母的乘积.
系数:单项式中的数字因数.
二、几点注意:
①单独的一个数或一个字母也是单项式;
②当一个单项式的系数是1或-1时,通常省略不写,如x2,-a2b等;
③圆周率π是常数,把它当作系数;
④如果单项式系数为0,它就是0次单项式;
⑤单项式次数只与字母指数有关.
一、单项式的有关概念:
当堂测试
当堂测试
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
