2.6 正多边形与圆 课件(32张PPT)
文档属性
| 名称 | 2.6 正多边形与圆 课件(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 10:25:13 | ||
图片预览








文档简介
2.6 正多边形与圆
第2章对称图形——圆
教学目标
01
认识正多边形,理解圆的内接正n边形、正n边形的外接圆的概念
02
理解正多边形的有关概念,掌握正多边形的有关计算
03
能借助尺规作出一些特殊的正多边形
正多边形与圆
01
二、定义
情境引入
我们已经学习过等边三角形(正三角形)、正方形(正四边形),正三角形、正四边形的各边相等,各角也相等。
螺帽的边缘
窗户的边框
生活中,各边相等、各角也相等的多边形的形象处处可见~
二、定义
情境引入
02
知识精讲
正多边形
正多边形:各边相等、各角也相等的多边形叫做正多边形。
情境引入
02
知识精讲
【思考1】已知:三边相等的三角形是正三角形,三角相等的三角形也是正三角形,问:各边相等的多边形是正多边形吗?或各角相等的多边形是正多边形吗?
各角相等的多边形不一定是正多边形
各边相等的多边形不一定是正多边形
02
二、定义
知识精讲
【思考2】如图,已知?O,
(1)用量角器把?O五等分,依次连接各等分点,得五边形ABCDE;(2)五边形ABCDE是正五边形吗?为什么?
如图,点A、B、C、D、E把?O五等分,
∵????????=????????=????????=????????=????????,
∴AB=BC=CD=DE=EA,????????????=???????????? ,
∴∠A =∠B,
同理:∠B=∠C=∠D=∠E,
∴五边形ABCDE是正五边形.
?
O
A
B
C
D
E
02
知识精讲
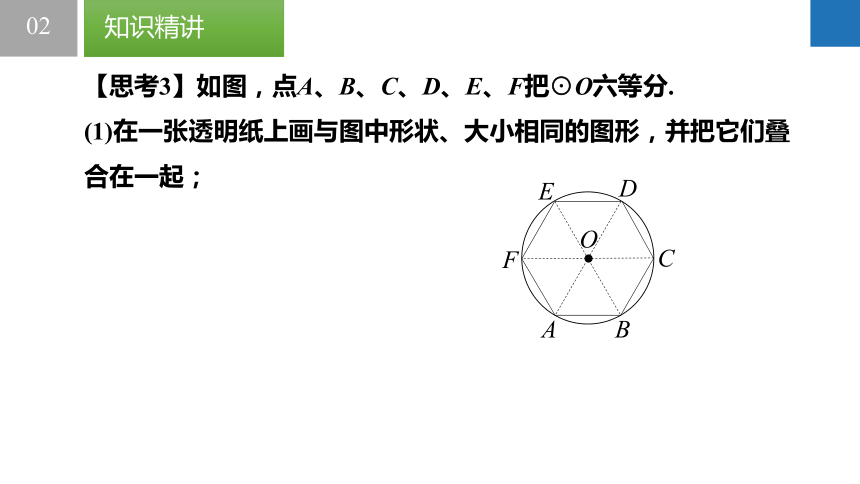
【思考3】如图,点A、B、C、D、E、F把?O六等分.
(1)在一张透明纸上画与图中形状、大小相同的图形,并把它们叠合在一起;
O
A
B
C
D
E
F
02
知识精讲
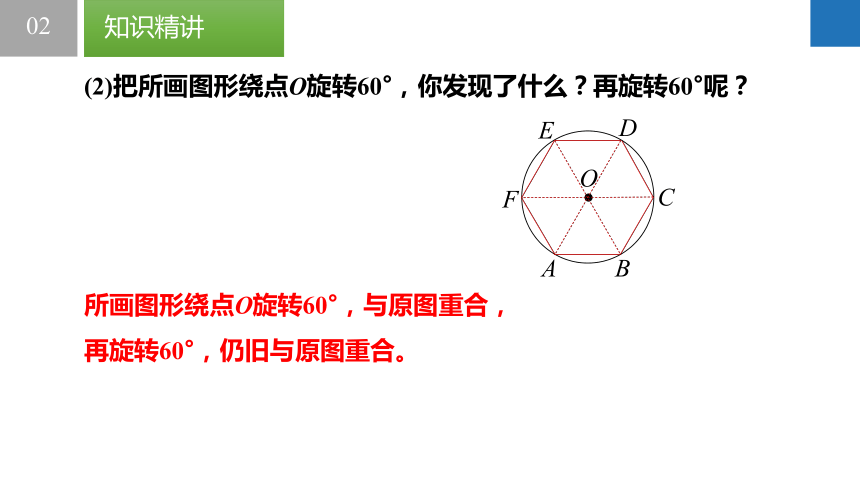
(2)把所画图形绕点O旋转60°,你发现了什么?再旋转60°呢?
O
A
B
C
D
E
F
所画图形绕点O旋转60°,与原图重合,
再旋转60°,仍旧与原图重合。
02
知识精讲
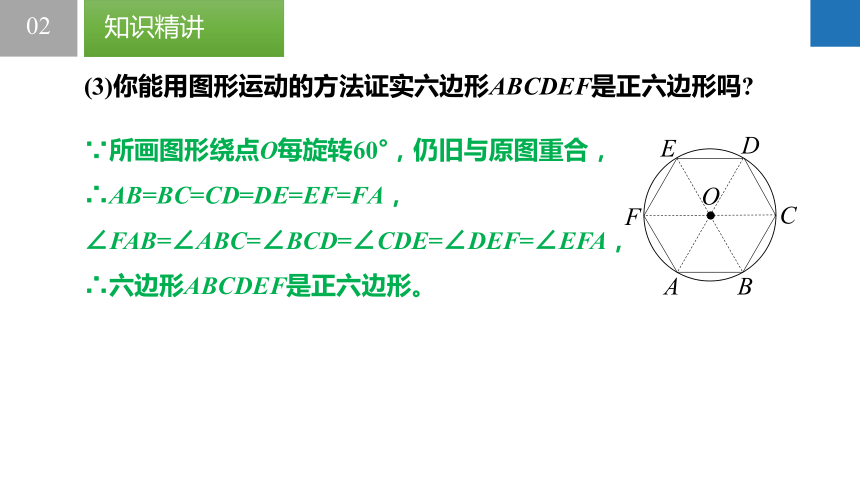
(3)你能用图形运动的方法证实六边形ABCDEF是正六边形吗?
O
A
B
C
D
E
F
∵所画图形绕点O每旋转60°,仍旧与原图重合,
∴AB=BC=CD=DE=EF=FA,
∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∴六边形ABCDEF是正六边形。
二、定义
情境引入
02
知识精讲
正多边形与圆
一般地,只要用量角器把一个圆n(n≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆是这个正n边形的外接圆。
二、定义
情境引入
02
知识精讲
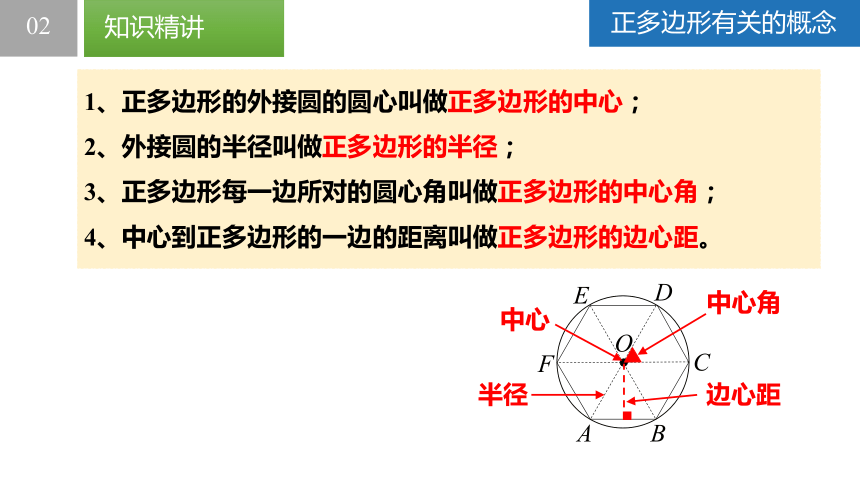
正多边形有关的概念
1、正多边形的外接圆的圆心叫做正多边形的中心;
2、外接圆的半径叫做正多边形的半径;
3、正多边形每一边所对的圆心角叫做正多边形的中心角;
4、中心到正多边形的一边的距离叫做正多边形的边心距。
O
A
B
C
D
E
F
中心
半径
中心角
边心距
02
知识精讲
【思考4】分别求半径为R的圆的内接正三角形、正方形、正六边形的边长、中心角、边心距、周长和面积。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正三角形
内接正方形
内接正六边形
边长
中心角
边心距
周长
面积
02
知识精讲
O
A
B
C
D
R
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正三角形
边长
中心角
边心距
周长
面积
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正三角形
边长
R
中心角
120°
边心距
周长
3R
面积
R2
02
知识精讲
O
A
B
C
D
R
E
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正方形
边长
中心角
边心距
周长
面积
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正方形
边长
R
中心角
90°
边心距
R
周长
4R
面积
2R2
02
知识精讲
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正六边形
边长
中心角
边心距
周长
面积
O
A
B
C
D
E
F
R
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正六边形
边长
R
中心角
60°
边心距
R
周长
6R
面积
R2
二、定义
情境引入
02
知识精讲
正多边形有关的计算
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}设正n边形的半径为R,边长为a,边心距为d,周长为C,面积为S
名称
公式
中心角
边心距
d=
周长
C=na
面积
S=Cd
02
知识精讲
【思考5】图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如果是轴对称图形,画出它的对称轴;如果是中心对称图形,找出它的对称中心。
轴对称图形:正三角形、正方形、正五边形、正六边形;
中心对称图形:正方形、正六边形。
02
知识精讲
【思考6】连接图中正多边形的半径和边心距,你发现了什么?
正三角形分成6个全等的直角三角形;
正方形分成8个全等的直角三角形;
正五边形分成10个全等的直角三角形;
正六边形分成12个全等的直角三角形。
二、定义
情境引入
02
知识精讲
正多边形的性质
1、轴对称性:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都经过正n边形的中心。
2、中心对称性:一个正多边形,如果有偶数条边,那么它是中心对称图形,对称中心就是这个正多边形的中心。
3、正多边形的半径和边心距把正n边形分成2n个全等的直角三角形。
03
二、定义
典例精析
例1、如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心.若∠ADB=18°,则这个正多边形的边数为________。
【分析】如图,连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数=????????????°????????°=10.
?
10
03
二、定义
典例精析
例2、已知?O的半径为6,则它的内接正三角形边心距为________。
【分析】如图,连接OB、OC,作OD⊥BC于D,
则∠ODB=90°,
∵边心角∠BOC=????????×360°=120°,OB=OC=6,
∴∠OBC=∠OCB=30°,
∴OD=????????OB=3.
?
3
03
二、定义
典例精析
例3、已知一个正多边形的中心角为45°,边长为5,那么这个正多边形的周长等于________。
【分析】∵该正多边形的中心角为45°,
∴正多边形的边数为:360°÷45°=8,
∴该正多边形的周长为:5×8=40.
40
03
二、定义
典例精析
例4、已知圆内接正六边形的边长是1,则该圆的内接正三角形的面积为________。
【分析】如图(二),
∵中心角=????????????°????=60°,
OA=OB,
∴△OAB是等边三角形,
∵圆内接正六边形边长为1,
∴圆的半径为1,
?
????????????
?
如图(一),
连接OB,过O作OD⊥BC于D,则∠OBC=30°,∴BD=????????OB=????????,∴BC=2BD=????,
∴圆的内接正三角形的面积=????????×????2=????????????.
?
正多边形的作法
情境引入
02
知识精讲
作图
用直尺和圆规可以作出一些特殊的正多边形~
1、作正方形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中作两条互相垂直的直径AC、BD.
2.依次连接A、B、C、D各点。
四边形ABCD就是所求作的正方形。
O
A
B
C
D
情境引入
02
知识精讲
【思考1】如何作正八边形?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中作两条互相垂直的直径AE、CG。
2.依次连接A、C、E、G各点。
3.过点O分别作AC、CE的垂线分别交于点B、交于点F和交于点D、交于点H。
4.依次连接A、B、C、D、E、F、G、H各点。
八边形ABCDEFGH就是所求作的正八边形。
O
A
C
E
G
B
D
F
H
情境引入
02
知识精讲
作图
2、作正六边形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中任意作一条直径AD。
2.分别以点A、D为圆心,?O的半径为半
径作弧,与?O相交于点B、F和点C、E。3.依次连接A、B、C、D、E、F各点。
六边形ABCDEF就是所求作的正六边形。
O
D
A
B
C
E
F
情境引入
02
知识精讲
【思考2】如何作正三角形?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中任意作一条直径BD。
2.分别以点A为圆心,?O的半径为半
径作弧,与?O相交于点A、C。
3.依次连接A、B、C各点。
三角形ABC就是所求作的正三角形。
O
A
C
B
D
情境引入
02
知识精讲
【思考3】如何作正十二边形?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中作两条互相垂直的直径AG、DJ。
2.分别以点A、G、D、J为圆心,?O的半径为半径作弧,与?O相交于点C、K和点E、I和点B、F和点H、L。
3.依次连接A、B、C、D、E、F、G、H、I、J、K、L各点。
十二边形ABCDEFGHIJKL就是所求作的正十二边形。
O
C
E
I
K
G
A
D
J
B
F
L
H
课后总结
正多边形:各边相等、各角也相等的多边形叫做正多边形。
一般地,只要用量角器把一个圆n(n≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆是这个正n边形的外接圆。
正多边形有关的概念:
1、正多边形的外接圆的圆心叫做正多边形的中心;
2、外接圆的半径叫做正多边形的半径;
3、正多边形每一边所对的圆心角叫做正多边形的中心角;
4、中心到正多边形的一边的距离叫做正多边形的边心距。
课后总结
正多边形有关的计算:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}设正n边形的半径为R,边长为a,边心距为d,周长为C,面积为S
名称
公式
中心角
边心距
d=
周长
C=na
面积
S=Cd
正多边形的性质:
1、轴对称性:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都经过正n边形的中心。
2、中心对称性:一个正多边形,如果有偶数条边,那么它是中心对称图形,对称中心就是这个正多边形的中心。
3、正多边形的半径和边心距把正n边形分成2n个全等的直角三角形。
第2章对称图形——圆
教学目标
01
认识正多边形,理解圆的内接正n边形、正n边形的外接圆的概念
02
理解正多边形的有关概念,掌握正多边形的有关计算
03
能借助尺规作出一些特殊的正多边形
正多边形与圆
01
二、定义
情境引入
我们已经学习过等边三角形(正三角形)、正方形(正四边形),正三角形、正四边形的各边相等,各角也相等。
螺帽的边缘
窗户的边框
生活中,各边相等、各角也相等的多边形的形象处处可见~
二、定义
情境引入
02
知识精讲
正多边形
正多边形:各边相等、各角也相等的多边形叫做正多边形。
情境引入
02
知识精讲
【思考1】已知:三边相等的三角形是正三角形,三角相等的三角形也是正三角形,问:各边相等的多边形是正多边形吗?或各角相等的多边形是正多边形吗?
各角相等的多边形不一定是正多边形
各边相等的多边形不一定是正多边形
02
二、定义
知识精讲
【思考2】如图,已知?O,
(1)用量角器把?O五等分,依次连接各等分点,得五边形ABCDE;(2)五边形ABCDE是正五边形吗?为什么?
如图,点A、B、C、D、E把?O五等分,
∵????????=????????=????????=????????=????????,
∴AB=BC=CD=DE=EA,????????????=???????????? ,
∴∠A =∠B,
同理:∠B=∠C=∠D=∠E,
∴五边形ABCDE是正五边形.
?
O
A
B
C
D
E
02
知识精讲
【思考3】如图,点A、B、C、D、E、F把?O六等分.
(1)在一张透明纸上画与图中形状、大小相同的图形,并把它们叠合在一起;
O
A
B
C
D
E
F
02
知识精讲
(2)把所画图形绕点O旋转60°,你发现了什么?再旋转60°呢?
O
A
B
C
D
E
F
所画图形绕点O旋转60°,与原图重合,
再旋转60°,仍旧与原图重合。
02
知识精讲
(3)你能用图形运动的方法证实六边形ABCDEF是正六边形吗?
O
A
B
C
D
E
F
∵所画图形绕点O每旋转60°,仍旧与原图重合,
∴AB=BC=CD=DE=EF=FA,
∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∴六边形ABCDEF是正六边形。
二、定义
情境引入
02
知识精讲
正多边形与圆
一般地,只要用量角器把一个圆n(n≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆是这个正n边形的外接圆。
二、定义
情境引入
02
知识精讲
正多边形有关的概念
1、正多边形的外接圆的圆心叫做正多边形的中心;
2、外接圆的半径叫做正多边形的半径;
3、正多边形每一边所对的圆心角叫做正多边形的中心角;
4、中心到正多边形的一边的距离叫做正多边形的边心距。
O
A
B
C
D
E
F
中心
半径
中心角
边心距
02
知识精讲
【思考4】分别求半径为R的圆的内接正三角形、正方形、正六边形的边长、中心角、边心距、周长和面积。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正三角形
内接正方形
内接正六边形
边长
中心角
边心距
周长
面积
02
知识精讲
O
A
B
C
D
R
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正三角形
边长
中心角
边心距
周长
面积
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正三角形
边长
R
中心角
120°
边心距
周长
3R
面积
R2
02
知识精讲
O
A
B
C
D
R
E
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正方形
边长
中心角
边心距
周长
面积
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正方形
边长
R
中心角
90°
边心距
R
周长
4R
面积
2R2
02
知识精讲
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正六边形
边长
中心角
边心距
周长
面积
O
A
B
C
D
E
F
R
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
内接正六边形
边长
R
中心角
60°
边心距
R
周长
6R
面积
R2
二、定义
情境引入
02
知识精讲
正多边形有关的计算
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}设正n边形的半径为R,边长为a,边心距为d,周长为C,面积为S
名称
公式
中心角
边心距
d=
周长
C=na
面积
S=Cd
02
知识精讲
【思考5】图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如果是轴对称图形,画出它的对称轴;如果是中心对称图形,找出它的对称中心。
轴对称图形:正三角形、正方形、正五边形、正六边形;
中心对称图形:正方形、正六边形。
02
知识精讲
【思考6】连接图中正多边形的半径和边心距,你发现了什么?
正三角形分成6个全等的直角三角形;
正方形分成8个全等的直角三角形;
正五边形分成10个全等的直角三角形;
正六边形分成12个全等的直角三角形。
二、定义
情境引入
02
知识精讲
正多边形的性质
1、轴对称性:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都经过正n边形的中心。
2、中心对称性:一个正多边形,如果有偶数条边,那么它是中心对称图形,对称中心就是这个正多边形的中心。
3、正多边形的半径和边心距把正n边形分成2n个全等的直角三角形。
03
二、定义
典例精析
例1、如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心.若∠ADB=18°,则这个正多边形的边数为________。
【分析】如图,连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数=????????????°????????°=10.
?
10
03
二、定义
典例精析
例2、已知?O的半径为6,则它的内接正三角形边心距为________。
【分析】如图,连接OB、OC,作OD⊥BC于D,
则∠ODB=90°,
∵边心角∠BOC=????????×360°=120°,OB=OC=6,
∴∠OBC=∠OCB=30°,
∴OD=????????OB=3.
?
3
03
二、定义
典例精析
例3、已知一个正多边形的中心角为45°,边长为5,那么这个正多边形的周长等于________。
【分析】∵该正多边形的中心角为45°,
∴正多边形的边数为:360°÷45°=8,
∴该正多边形的周长为:5×8=40.
40
03
二、定义
典例精析
例4、已知圆内接正六边形的边长是1,则该圆的内接正三角形的面积为________。
【分析】如图(二),
∵中心角=????????????°????=60°,
OA=OB,
∴△OAB是等边三角形,
∵圆内接正六边形边长为1,
∴圆的半径为1,
?
????????????
?
如图(一),
连接OB,过O作OD⊥BC于D,则∠OBC=30°,∴BD=????????OB=????????,∴BC=2BD=????,
∴圆的内接正三角形的面积=????????×????2=????????????.
?
正多边形的作法
情境引入
02
知识精讲
作图
用直尺和圆规可以作出一些特殊的正多边形~
1、作正方形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中作两条互相垂直的直径AC、BD.
2.依次连接A、B、C、D各点。
四边形ABCD就是所求作的正方形。
O
A
B
C
D
情境引入
02
知识精讲
【思考1】如何作正八边形?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中作两条互相垂直的直径AE、CG。
2.依次连接A、C、E、G各点。
3.过点O分别作AC、CE的垂线分别交于点B、交于点F和交于点D、交于点H。
4.依次连接A、B、C、D、E、F、G、H各点。
八边形ABCDEFGH就是所求作的正八边形。
O
A
C
E
G
B
D
F
H
情境引入
02
知识精讲
作图
2、作正六边形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中任意作一条直径AD。
2.分别以点A、D为圆心,?O的半径为半
径作弧,与?O相交于点B、F和点C、E。3.依次连接A、B、C、D、E、F各点。
六边形ABCDEF就是所求作的正六边形。
O
D
A
B
C
E
F
情境引入
02
知识精讲
【思考2】如何作正三角形?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中任意作一条直径BD。
2.分别以点A为圆心,?O的半径为半
径作弧,与?O相交于点A、C。
3.依次连接A、B、C各点。
三角形ABC就是所求作的正三角形。
O
A
C
B
D
情境引入
02
知识精讲
【思考3】如何作正十二边形?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作法
图形
1.在?O中作两条互相垂直的直径AG、DJ。
2.分别以点A、G、D、J为圆心,?O的半径为半径作弧,与?O相交于点C、K和点E、I和点B、F和点H、L。
3.依次连接A、B、C、D、E、F、G、H、I、J、K、L各点。
十二边形ABCDEFGHIJKL就是所求作的正十二边形。
O
C
E
I
K
G
A
D
J
B
F
L
H
课后总结
正多边形:各边相等、各角也相等的多边形叫做正多边形。
一般地,只要用量角器把一个圆n(n≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆是这个正n边形的外接圆。
正多边形有关的概念:
1、正多边形的外接圆的圆心叫做正多边形的中心;
2、外接圆的半径叫做正多边形的半径;
3、正多边形每一边所对的圆心角叫做正多边形的中心角;
4、中心到正多边形的一边的距离叫做正多边形的边心距。
课后总结
正多边形有关的计算:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}设正n边形的半径为R,边长为a,边心距为d,周长为C,面积为S
名称
公式
中心角
边心距
d=
周长
C=na
面积
S=Cd
正多边形的性质:
1、轴对称性:正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都经过正n边形的中心。
2、中心对称性:一个正多边形,如果有偶数条边,那么它是中心对称图形,对称中心就是这个正多边形的中心。
3、正多边形的半径和边心距把正n边形分成2n个全等的直角三角形。
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
