3.3勾股定理的简单应用 课件(28张PPT)
文档属性
| 名称 | 3.3勾股定理的简单应用 课件(28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 10:36:56 | ||
图片预览






文档简介
(共28张PPT)
第3章 · 勾股定理
3.3 勾股定理的简单应用
学习目标
1. 能应用勾股定理及其逆定理解决简单的实际问题;
2. 感受“转化”“建模”的数学思想,提高分析问题、解决问题的能力.
知识回顾
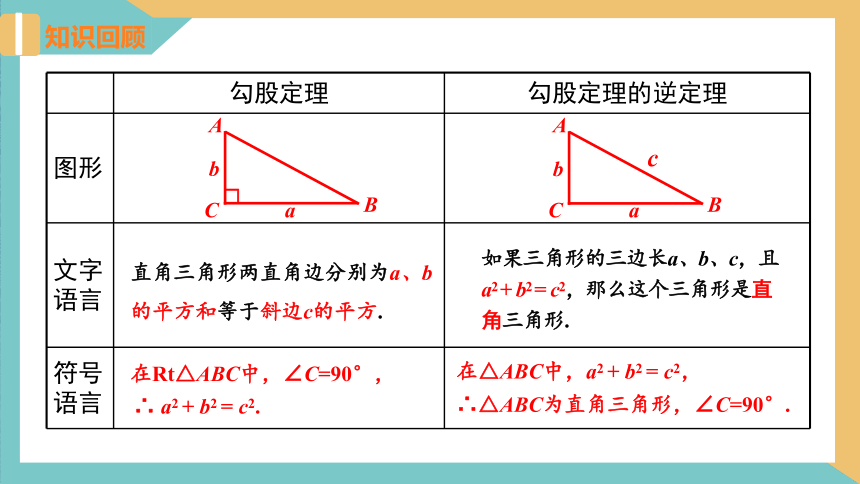
勾股定理 勾股定理的逆定理
图形
文字语言
符号语言
A
b
a
C
B
∟
在Rt△ABC中,∠C=90°,
∴ a2 + b2 = c2.
A
b
a
C
B
c
在△ABC中,a2 + b2 = c2,
∴△ABC为直角三角形,∠C=90°.
如果三角形的三边长a、b、c,且a2 + b2 = c2,那么这个三角形是直角三角形.
直角三角形两直角边分别为a、b的平方和等于斜边c的平方.
从远处看斜拉桥,可以发现有许多直角三角形.
已知桥面上以上的索塔AB的高,怎样计算拉索AC、AD、AE、AF、AG的长?
分别测量出BC、BD、BE、BF、BG的长度,根据勾股定理计算出AC、AD、AE、AF、AG的长
讨论与交流
例题讲解
例1 九章算术中的“折竹”问题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
A
C
B
x
(10-x)
3
┐
解:如图,竹子在点AC处折断,竹梢点B着地,△ABC是直角三角形.
设OA=x尺,则AB=(10-x)尺.
由勾股定理,得,
∴OA2+OB2=AB2,
∴x2+32=(10-x)2.
∴OA=x=4.55(尺)
1.构造直角三角形
3.用勾股定理列出方程
4.解方程
5.检验、写出答案
2.设出未知数
∴折断处离地面4.55尺.
例题讲解
例2 如图, 在△ABC中, AB=26, BC=20, BC边上的中线AD=24, 求AC.
D
C
B
A
26
20
24
∵AD2+BD2=576+100=676,
AB 2=262=676,
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
还有其他方法求AC吗?
能求出△ABC的周长和面积吗
∟
例题讲解
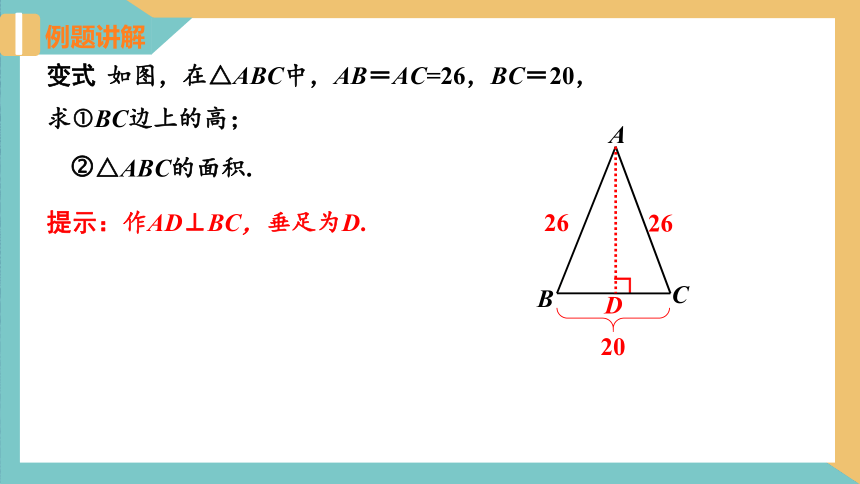
变式 如图,在△ABC中,AB=AC=26,BC=20,
求 BC边上的高;
C
B
A
26
20
26
△ABC的面积.
D
提示:作AD⊥BC,垂足为D.
新知巩固
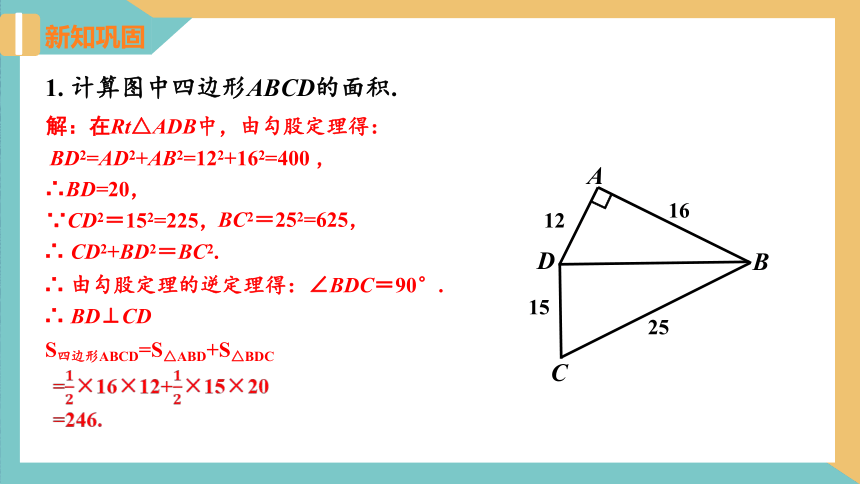
1. 计算图中四边形ABCD的面积.
解:在Rt△ADB中,由勾股定理得:
BD2=AD2+AB2=122+162=400 ,
∴BD=20,
∵CD2=152=225,
∴ CD2+BD2=BC2.
∴ 由勾股定理的逆定理得:∠BDC=90°.
∴ BD⊥CD
S四边形ABCD=S△ABD+S△BDC
D
C
B
A
∟
12
16
15
25
BC2=252=625,
新知巩固
2. 一个三角形三边长的比为3:4:5,它的周长是60cm. 求这个三角形的面积.
例3 如图,四边形ABCD是学校的一块空地,经数学兴趣小组的测量可知,∠B=90°,BC=3米,AB=4米,CD=13米,AD=12米.为了提高校园的绿化面积,现学校决定在空地内铺草坪,若铺设每平方米草坪需要30元,则将这块空地全部铺满一层草坪的费用是多少?
A
B
C
D
3
4
12
13
例题讲解
∟
例题讲解
例4 如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
D
B
A
C
E
x
10-x
6cm
10-x
10cm
∟
关于折叠问题,要紧扣折叠前后的对应边,对应角相等.
解:如图,连接BE.
∵A与B折叠后重合,
∴直线DE是线段AB的垂直平分线.
∴BE=AE.
设CE=x,则BE=AE=10-x,在Rt△EBC中,由勾股定理得:
BE2=CE2+BC2,
∴(10-x)2=x2+62,x=3.2.
∴CE=3.2cm.
1. 有一块空白地,如图,∠ADC=90°,CD=6 m,AD=8 m,AB=26 m,BC=24 m.试求这块空白地的面积.
A
D
B
C
解:连接AC.在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262=AB2,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S空白部分=S△ACB-S△ACD
=120-24
=96.
∟
新知巩固
新知巩固
2. 如图,有一块直角三角形纸片,两直角边AB=6cm,BC=8cm,现将三角形纸片沿直线AD折叠,使点B落在AC上,与点E重合,求DE的长度.
B
D
A
C
E
xcm
xcm
(8-x)cm
4cm
6cm
8cm
10cm
6cm
讨论与交流
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状.
勾股定理的前提必须是直角三角形;
课堂小结
勾股定理的简单应用
几何问题中的应用
求三角形的边长、求图形的面积等
实际问题中的应用
求长度、距离、宽度、高度等
关键:构造直角三角形
当堂检测
1.如图,将一根长13厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为( )厘米.
A.1 B.2 C.3 D.4
C
13cm
8cm
6cm
?cm
当堂检测
2.如图,由于台风影响,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是 米.
8
当堂检测
3.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.设芦苇长x尺,则可列方程__________________.
x尺
(x-1)尺
5尺
(x-1)2+52=x2
当堂检测
4.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了________m.
8m
2m
8m
A
B
C
8
6
10
10
┐
当堂检测
图(1)
图(2)
B
C
x
x+1
5
5.某八(2)班的学生想知道学校旗杆的高度,如图(1),他们发现旗杆上的绳子垂到地面还多1米,如图(2),当他们把绳子的下端拉开5米后,发现下端刚好接触地面,你们知道,他们是用什么方法求出旗杆的高度和绳子的长度的吗?
A
┐
当堂检测
6. 用一张长方形纸片ABCD进行折纸,已知纸片宽AB=8cm,长BC=10cm,折叠时,顶点D落在BC边上点F处,想一想此时EC有多长?
A
D
C
B
E
F
8cm
10cm
xcm
(8-x)cm
10cm
10cm
6cm
4cm
(8-x)cm
当堂检测
7. 如图,一架竹梯长13 m,斜靠在一面墙上,梯子底端离墙5 m.
(1)求这个梯子顶端距地面的高度;
(2)如果梯子的顶端下滑7 m,那么梯子的底部在水平方向也滑动了7 m吗?为什么?
解:(1)∵AO⊥BO,AB=13 m,OB=5 m,∴AO=12 m,即梯子顶端距地面的高度为12 m.
(2)梯子底部在水平方向也滑动了7 m.理由如下:
∵AC=7 m,∴OC=AO-AC=5 m.
又CD=AB=13 m,
∴OD=12 m,
∴BD=OD-OB=12-5=7(cm),
∴梯子的底部在水平方向也滑动了7 m.
当堂检测
8. 如图,甲、乙两船从港口A同时出发,甲船以16海里/时的速度向南偏东40°的方向航行,乙船以12海里/时的速度向另一方向航行,3小时后,甲船到达B岛,乙船到达C岛,若B,C两岛相距60海里,通过计算说明乙船航行的方向.
A
北
东
C
B
解:如图,由已知可得AB=16×3=48(海里),AC=12×3=36(海里),BC=60海里.
∵482+362=602,
∴AB2+AC2=BC2.
∴△ABC为直角三角形,且∠BAC=90°.
∵∠EAB=40°,
∴∠FAC=180°-40°-90°=50°.
∴乙船是沿北偏东50°方向航行的.
拓展延伸
1.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
F
A
B
C
C
E
18cm
30cm
两点的距离最短问题
—转化成平面展开图中两点之间的连线段最短.
拓展延伸
变式1 如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱表面爬到B点,那么它所行的最短路线的长是多少?
解:如图①,
AB2=AC2+BC2=32+(3+8)2=130.
如图②,
AB2=AC2+BC2=62+82=100.
∵130>100,
∴AB=10.
答:它所行的最短路线的长是10.
B
A
B
A
B
3
3
8
A
B
C
图①
图②
8
P
A
Q
拓展延伸
变式2 如图,长方体的长为4 cm,宽为2 cm,高为5 cm. 若一只蚂蚁从点P开始经过4个侧面爬行一圈到达点Q,求蚂蚁爬行的最短路径长.
Q
4cm
5cm
P
A
2cm
解:将长方体的侧面展开如图所示:
∵长方体的长为4 cm,宽为2 cm,
高为5 cm,
∴PA=4+2+4+2=12(cm),QA=5 cm.
∴PQ2=PA2+AQ2=169.
∴PQ=13(cm).答:蚂蚁爬行的最短路径长为13 cm.
拓展延伸
变式3 如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少?
2
0.3
0.2
A
B
A
B
C
2m
(0.2×3+0.3×3)m
拓展延伸
2.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
A
B
C
D
第3章 · 勾股定理
3.3 勾股定理的简单应用
学习目标
1. 能应用勾股定理及其逆定理解决简单的实际问题;
2. 感受“转化”“建模”的数学思想,提高分析问题、解决问题的能力.
知识回顾
勾股定理 勾股定理的逆定理
图形
文字语言
符号语言
A
b
a
C
B
∟
在Rt△ABC中,∠C=90°,
∴ a2 + b2 = c2.
A
b
a
C
B
c
在△ABC中,a2 + b2 = c2,
∴△ABC为直角三角形,∠C=90°.
如果三角形的三边长a、b、c,且a2 + b2 = c2,那么这个三角形是直角三角形.
直角三角形两直角边分别为a、b的平方和等于斜边c的平方.
从远处看斜拉桥,可以发现有许多直角三角形.
已知桥面上以上的索塔AB的高,怎样计算拉索AC、AD、AE、AF、AG的长?
分别测量出BC、BD、BE、BF、BG的长度,根据勾股定理计算出AC、AD、AE、AF、AG的长
讨论与交流
例题讲解
例1 九章算术中的“折竹”问题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?意思是:有一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?
A
C
B
x
(10-x)
3
┐
解:如图,竹子在点AC处折断,竹梢点B着地,△ABC是直角三角形.
设OA=x尺,则AB=(10-x)尺.
由勾股定理,得,
∴OA2+OB2=AB2,
∴x2+32=(10-x)2.
∴OA=x=4.55(尺)
1.构造直角三角形
3.用勾股定理列出方程
4.解方程
5.检验、写出答案
2.设出未知数
∴折断处离地面4.55尺.
例题讲解
例2 如图, 在△ABC中, AB=26, BC=20, BC边上的中线AD=24, 求AC.
D
C
B
A
26
20
24
∵AD2+BD2=576+100=676,
AB 2=262=676,
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
还有其他方法求AC吗?
能求出△ABC的周长和面积吗
∟
例题讲解
变式 如图,在△ABC中,AB=AC=26,BC=20,
求 BC边上的高;
C
B
A
26
20
26
△ABC的面积.
D
提示:作AD⊥BC,垂足为D.
新知巩固
1. 计算图中四边形ABCD的面积.
解:在Rt△ADB中,由勾股定理得:
BD2=AD2+AB2=122+162=400 ,
∴BD=20,
∵CD2=152=225,
∴ CD2+BD2=BC2.
∴ 由勾股定理的逆定理得:∠BDC=90°.
∴ BD⊥CD
S四边形ABCD=S△ABD+S△BDC
D
C
B
A
∟
12
16
15
25
BC2=252=625,
新知巩固
2. 一个三角形三边长的比为3:4:5,它的周长是60cm. 求这个三角形的面积.
例3 如图,四边形ABCD是学校的一块空地,经数学兴趣小组的测量可知,∠B=90°,BC=3米,AB=4米,CD=13米,AD=12米.为了提高校园的绿化面积,现学校决定在空地内铺草坪,若铺设每平方米草坪需要30元,则将这块空地全部铺满一层草坪的费用是多少?
A
B
C
D
3
4
12
13
例题讲解
∟
例题讲解
例4 如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
D
B
A
C
E
x
10-x
6cm
10-x
10cm
∟
关于折叠问题,要紧扣折叠前后的对应边,对应角相等.
解:如图,连接BE.
∵A与B折叠后重合,
∴直线DE是线段AB的垂直平分线.
∴BE=AE.
设CE=x,则BE=AE=10-x,在Rt△EBC中,由勾股定理得:
BE2=CE2+BC2,
∴(10-x)2=x2+62,x=3.2.
∴CE=3.2cm.
1. 有一块空白地,如图,∠ADC=90°,CD=6 m,AD=8 m,AB=26 m,BC=24 m.试求这块空白地的面积.
A
D
B
C
解:连接AC.在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262=AB2,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S空白部分=S△ACB-S△ACD
=120-24
=96.
∟
新知巩固
新知巩固
2. 如图,有一块直角三角形纸片,两直角边AB=6cm,BC=8cm,现将三角形纸片沿直线AD折叠,使点B落在AC上,与点E重合,求DE的长度.
B
D
A
C
E
xcm
xcm
(8-x)cm
4cm
6cm
8cm
10cm
6cm
讨论与交流
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状.
勾股定理的前提必须是直角三角形;
课堂小结
勾股定理的简单应用
几何问题中的应用
求三角形的边长、求图形的面积等
实际问题中的应用
求长度、距离、宽度、高度等
关键:构造直角三角形
当堂检测
1.如图,将一根长13厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为( )厘米.
A.1 B.2 C.3 D.4
C
13cm
8cm
6cm
?cm
当堂检测
2.如图,由于台风影响,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是 米.
8
当堂检测
3.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.设芦苇长x尺,则可列方程__________________.
x尺
(x-1)尺
5尺
(x-1)2+52=x2
当堂检测
4.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了________m.
8m
2m
8m
A
B
C
8
6
10
10
┐
当堂检测
图(1)
图(2)
B
C
x
x+1
5
5.某八(2)班的学生想知道学校旗杆的高度,如图(1),他们发现旗杆上的绳子垂到地面还多1米,如图(2),当他们把绳子的下端拉开5米后,发现下端刚好接触地面,你们知道,他们是用什么方法求出旗杆的高度和绳子的长度的吗?
A
┐
当堂检测
6. 用一张长方形纸片ABCD进行折纸,已知纸片宽AB=8cm,长BC=10cm,折叠时,顶点D落在BC边上点F处,想一想此时EC有多长?
A
D
C
B
E
F
8cm
10cm
xcm
(8-x)cm
10cm
10cm
6cm
4cm
(8-x)cm
当堂检测
7. 如图,一架竹梯长13 m,斜靠在一面墙上,梯子底端离墙5 m.
(1)求这个梯子顶端距地面的高度;
(2)如果梯子的顶端下滑7 m,那么梯子的底部在水平方向也滑动了7 m吗?为什么?
解:(1)∵AO⊥BO,AB=13 m,OB=5 m,∴AO=12 m,即梯子顶端距地面的高度为12 m.
(2)梯子底部在水平方向也滑动了7 m.理由如下:
∵AC=7 m,∴OC=AO-AC=5 m.
又CD=AB=13 m,
∴OD=12 m,
∴BD=OD-OB=12-5=7(cm),
∴梯子的底部在水平方向也滑动了7 m.
当堂检测
8. 如图,甲、乙两船从港口A同时出发,甲船以16海里/时的速度向南偏东40°的方向航行,乙船以12海里/时的速度向另一方向航行,3小时后,甲船到达B岛,乙船到达C岛,若B,C两岛相距60海里,通过计算说明乙船航行的方向.
A
北
东
C
B
解:如图,由已知可得AB=16×3=48(海里),AC=12×3=36(海里),BC=60海里.
∵482+362=602,
∴AB2+AC2=BC2.
∴△ABC为直角三角形,且∠BAC=90°.
∵∠EAB=40°,
∴∠FAC=180°-40°-90°=50°.
∴乙船是沿北偏东50°方向航行的.
拓展延伸
1.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
F
A
B
C
C
E
18cm
30cm
两点的距离最短问题
—转化成平面展开图中两点之间的连线段最短.
拓展延伸
变式1 如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱表面爬到B点,那么它所行的最短路线的长是多少?
解:如图①,
AB2=AC2+BC2=32+(3+8)2=130.
如图②,
AB2=AC2+BC2=62+82=100.
∵130>100,
∴AB=10.
答:它所行的最短路线的长是10.
B
A
B
A
B
3
3
8
A
B
C
图①
图②
8
P
A
Q
拓展延伸
变式2 如图,长方体的长为4 cm,宽为2 cm,高为5 cm. 若一只蚂蚁从点P开始经过4个侧面爬行一圈到达点Q,求蚂蚁爬行的最短路径长.
Q
4cm
5cm
P
A
2cm
解:将长方体的侧面展开如图所示:
∵长方体的长为4 cm,宽为2 cm,
高为5 cm,
∴PA=4+2+4+2=12(cm),QA=5 cm.
∴PQ2=PA2+AQ2=169.
∴PQ=13(cm).答:蚂蚁爬行的最短路径长为13 cm.
拓展延伸
变式3 如图,是一个三级台阶,它的每一级的长、宽、高分别为2m、0.3m、0.2m,A和B是台阶上两个相对的顶点,A点有一只蚂蚁,想到B点去吃可口的食物,问蚂蚁沿着台阶爬行到B点的最短路程是多少?
2
0.3
0.2
A
B
A
B
C
2m
(0.2×3+0.3×3)m
拓展延伸
2.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.
A
B
C
D
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
