12.1全等三角形 课件(29张PPT)
图片预览




文档简介
(共29张PPT)
新课标 人教版 八年级上册
2023-2024学年度上学期人教版精品课件
第十二章 全等角形
12.1 全等三角形
学习目标
1.理解全等形的定义.
2.掌握全等三角形的定义及性质,能正确表示两个全等三角形,能找准全等三角形的对应边、对应角.
3.利用全等三角形的性质进行简单的推理与计算,并解决一些实际问题.
情境引入
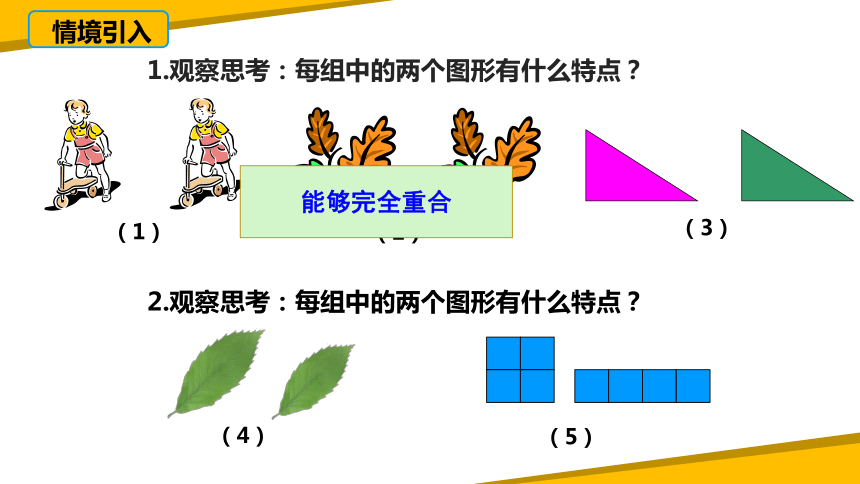
1.观察思考:每组中的两个图形有什么特点?
(1)
(2)
(3)
2.观察思考:每组中的两个图形有什么特点?
(4)
(5)
能够完全重合
探究新知
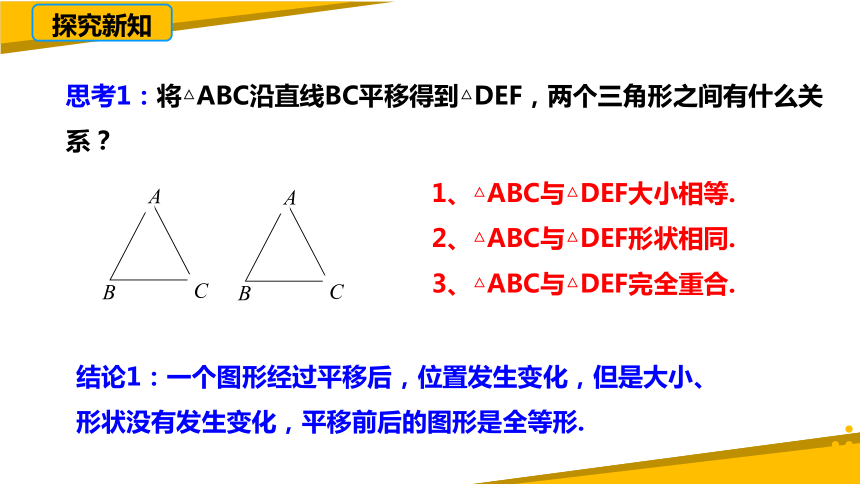
思考1:将△ABC沿直线BC平移得到△DEF,两个三角形之间有什么关系?
A
B
C
A
B
C
1、△ABC与△DEF大小相等.
2、△ABC与△DEF形状相同.
3、△ABC与△DEF完全重合.
结论1:一个图形经过平移后,位置发生变化,但是大小、形状没有发生变化,平移前后的图形是全等形.
探究新知
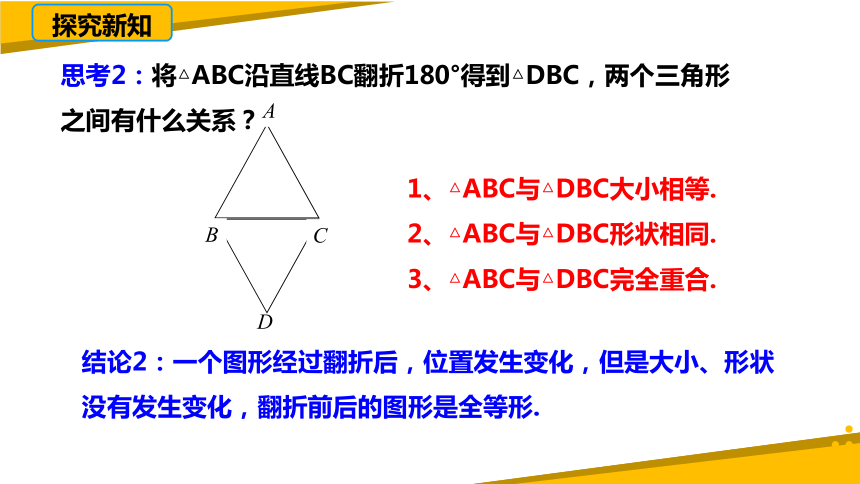
1、△ABC与△DBC大小相等.
2、△ABC与△DBC形状相同.
3、△ABC与△DBC完全重合.
A
B
C
结论2:一个图形经过翻折后,位置发生变化,但是大小、形状没有发生变化,翻折前后的图形是全等形.
D
思考2:将△ABC沿直线BC翻折180°得到△DBC,两个三角形之间有什么关系?
探究新知
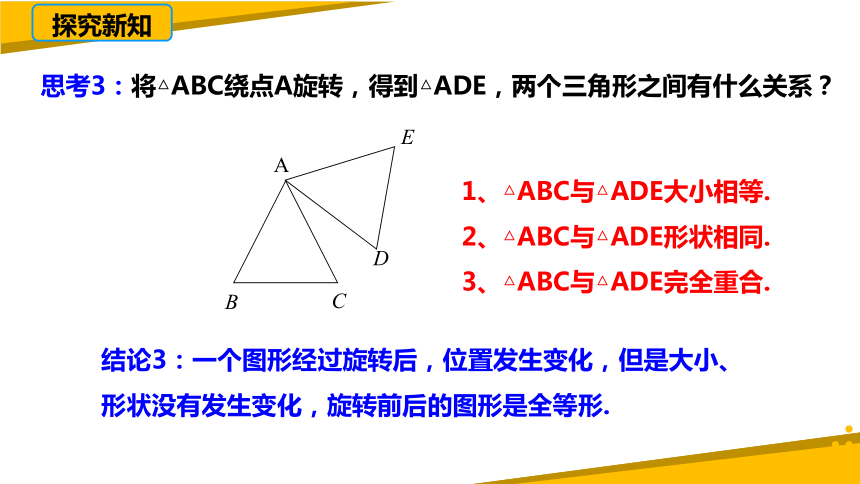
思考3:将△ABC绕点A旋转,得到△ADE,两个三角形之间有什么关系?
B
C
1、△ABC与△ADE大小相等.
2、△ABC与△ADE形状相同.
3、△ABC与△ADE完全重合.
结论3:一个图形经过旋转后,位置发生变化,但是大小、形状没有发生变化,旋转前后的图形是全等形.
A
E
D
探究新知
全等形的概念:
能够完全重合的两个图形叫做全等形.
全等形的性质:
如果两个图形全等,它们的形状和大小一定都相等.
一个图形经过平移、翻折、旋转后,位置发生变化,但是大小、形状没有发生变化,平移、翻折、旋转前后的图形是全等形.
归纳:
探究新知
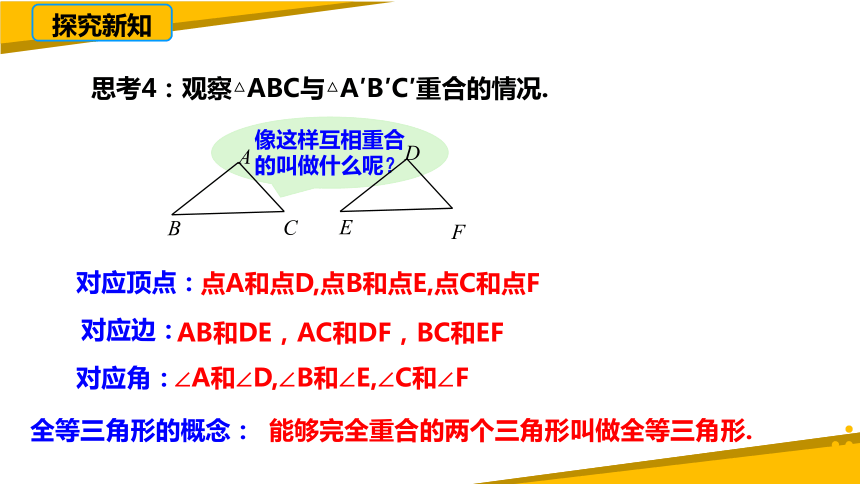
思考4:观察△ABC与△A′B′C′重合的情况.
像这样互相重合的叫做什么呢?
点A和点D,点B和点E,点C和点F
AB和DE,AC和DF,BC和EF
∠A和∠D,∠B和∠E,∠C和∠F
对应顶点:
对应边:
对应角:
A
B
C
D
E
F
全等三角形的概念:
能够完全重合的两个三角形叫做全等三角形.
探究新知
全等用符号“≌”表示,读作“全等于”.△ABC与△DEF全等,记作△ABC≌△DEF ,读作“三角形ABC全等于三角形DEF”.
全等三角形的表示:
注意:书写时应把对应顶点写在相对应的位置上.
如果两个三角形全等,它们的对应边、对应角有怎样的大小关系?
探究新知
A
B
C
D
E
F
全等三角形的性质:
几何符号表示:
∵△ABC≌△DEF
∴AB=DE,AC=DF,BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的对应边相等,全等三角形的对应角相等.
随堂练习
1. 下面哪些图形是全等图形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
随堂练习
2. 如图所示:△ABC≌ △ADE,写出其对应顶点,对应边和对应角.
解:对应顶点:点A和点A,点B和点D,点C和点E
对应角:∠BAC与∠DAE, ∠B与∠D, ∠C与∠E
对应边:AB与AD, BC与DE,AC与AE
随堂练习
3.如图,若把△ABC 绕A点顺时针旋转一定的角度得到△ADE,已知∠ BAC=85°,∠BAD=35°,求∠BAE的度数.
解: ∵ △ADE是由△ABC旋转而得到的
∴ △ADE ≌ △ABC
∴ ∠DAE= ∠BAC=85 °
∴ ∠BAE= ∠DAE —∠BAD
∵ ∠BAD=35°
=85°—35°
=50°
随堂练习
4.如图,△ABC≌△DEF,∠A=70 ,∠B=50 ,BF=4,EF=7,
求∠DEF的度数和CF的长.
A
D
C
F
B
E
解:∵△ABC≌△DEF,∠A=70 ,∠B=50 ,
BF=4,EF=7,
∴∠DEF=∠B=50 ,BC=EF=7,
∴CF=BC-BF=7-4=3.
中考链接
中考链接
中考链接
课堂小结
全等三角形
定义
能够完全重合的两个三角形.
表示方法
有关概念
对应顶点、对应边、对应角
性质
对应边相等、对应角相等
当堂测试
当堂测试
当堂测试
分层作业
分层作业
分层作业
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 八年级上册
2023-2024学年度上学期人教版精品课件
第十二章 全等角形
12.1 全等三角形
学习目标
1.理解全等形的定义.
2.掌握全等三角形的定义及性质,能正确表示两个全等三角形,能找准全等三角形的对应边、对应角.
3.利用全等三角形的性质进行简单的推理与计算,并解决一些实际问题.
情境引入
1.观察思考:每组中的两个图形有什么特点?
(1)
(2)
(3)
2.观察思考:每组中的两个图形有什么特点?
(4)
(5)
能够完全重合
探究新知
思考1:将△ABC沿直线BC平移得到△DEF,两个三角形之间有什么关系?
A
B
C
A
B
C
1、△ABC与△DEF大小相等.
2、△ABC与△DEF形状相同.
3、△ABC与△DEF完全重合.
结论1:一个图形经过平移后,位置发生变化,但是大小、形状没有发生变化,平移前后的图形是全等形.
探究新知
1、△ABC与△DBC大小相等.
2、△ABC与△DBC形状相同.
3、△ABC与△DBC完全重合.
A
B
C
结论2:一个图形经过翻折后,位置发生变化,但是大小、形状没有发生变化,翻折前后的图形是全等形.
D
思考2:将△ABC沿直线BC翻折180°得到△DBC,两个三角形之间有什么关系?
探究新知
思考3:将△ABC绕点A旋转,得到△ADE,两个三角形之间有什么关系?
B
C
1、△ABC与△ADE大小相等.
2、△ABC与△ADE形状相同.
3、△ABC与△ADE完全重合.
结论3:一个图形经过旋转后,位置发生变化,但是大小、形状没有发生变化,旋转前后的图形是全等形.
A
E
D
探究新知
全等形的概念:
能够完全重合的两个图形叫做全等形.
全等形的性质:
如果两个图形全等,它们的形状和大小一定都相等.
一个图形经过平移、翻折、旋转后,位置发生变化,但是大小、形状没有发生变化,平移、翻折、旋转前后的图形是全等形.
归纳:
探究新知
思考4:观察△ABC与△A′B′C′重合的情况.
像这样互相重合的叫做什么呢?
点A和点D,点B和点E,点C和点F
AB和DE,AC和DF,BC和EF
∠A和∠D,∠B和∠E,∠C和∠F
对应顶点:
对应边:
对应角:
A
B
C
D
E
F
全等三角形的概念:
能够完全重合的两个三角形叫做全等三角形.
探究新知
全等用符号“≌”表示,读作“全等于”.△ABC与△DEF全等,记作△ABC≌△DEF ,读作“三角形ABC全等于三角形DEF”.
全等三角形的表示:
注意:书写时应把对应顶点写在相对应的位置上.
如果两个三角形全等,它们的对应边、对应角有怎样的大小关系?
探究新知
A
B
C
D
E
F
全等三角形的性质:
几何符号表示:
∵△ABC≌△DEF
∴AB=DE,AC=DF,BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形的对应边相等,全等三角形的对应角相等.
随堂练习
1. 下面哪些图形是全等图形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
随堂练习
2. 如图所示:△ABC≌ △ADE,写出其对应顶点,对应边和对应角.
解:对应顶点:点A和点A,点B和点D,点C和点E
对应角:∠BAC与∠DAE, ∠B与∠D, ∠C与∠E
对应边:AB与AD, BC与DE,AC与AE
随堂练习
3.如图,若把△ABC 绕A点顺时针旋转一定的角度得到△ADE,已知∠ BAC=85°,∠BAD=35°,求∠BAE的度数.
解: ∵ △ADE是由△ABC旋转而得到的
∴ △ADE ≌ △ABC
∴ ∠DAE= ∠BAC=85 °
∴ ∠BAE= ∠DAE —∠BAD
∵ ∠BAD=35°
=85°—35°
=50°
随堂练习
4.如图,△ABC≌△DEF,∠A=70 ,∠B=50 ,BF=4,EF=7,
求∠DEF的度数和CF的长.
A
D
C
F
B
E
解:∵△ABC≌△DEF,∠A=70 ,∠B=50 ,
BF=4,EF=7,
∴∠DEF=∠B=50 ,BC=EF=7,
∴CF=BC-BF=7-4=3.
中考链接
中考链接
中考链接
课堂小结
全等三角形
定义
能够完全重合的两个三角形.
表示方法
有关概念
对应顶点、对应边、对应角
性质
对应边相等、对应角相等
当堂测试
当堂测试
当堂测试
分层作业
分层作业
分层作业
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
