等差数列前n项和
图片预览








文档简介
课件21张PPT。等差数列的前n项和等差数列的前n项和教学重点:等差数列前n项和公式及其应用。教学难点:获得推导公式的思路教学方法:启发诱导 自学探究知识目标:掌握等差数列的前n项和公式,
并能运用公式解决简单问题。 情感目标:提高分析和解决问题的能力,
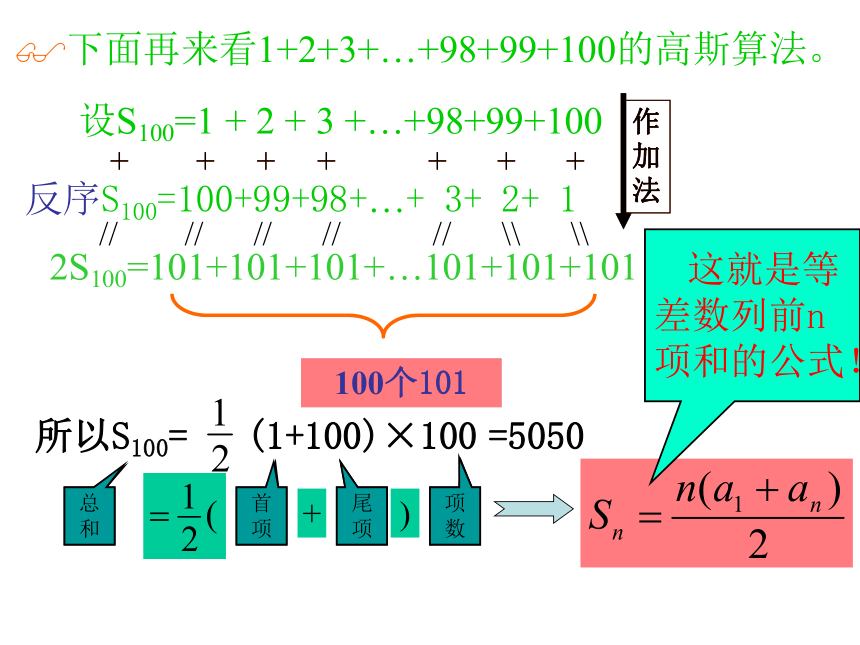
培养创新精神,强化实践能力。独立思考以下问题:问题一: 1+2+3+······+100=?问题二: 1+2+3+······+99=?问题三: 1+2+3+······+n=?等差数列的前n项和德国古代著名数学家高斯9岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?赶快开动脑筋,想一想!1+2+3+···+100=??下面再来看1+2+3+…+98+99+100的高斯算法。设S100=1 + 2 + 3 +…+98+99+100反序S100=100+99+98+…+ 3+ 2+ 1多少个101 ?100个101所以S100=(1+100)×100??首项尾项?总
和?项数 这就是等差数列前n项和的公式!=5050等差数列的前n项和公式的推导由 an=a1+(n-1)d am=an-(n-m)d 得等差数列的前n项和公式的推导等差数列的前n项和公式的其它形式类比梯形面积公式记忆等差数列的前n项和例题1. 根据下列条件,求相应的等差数列 的 根据下列条件,求相应的等差数列 的公式应用选用公式公式应用变用公式 等差数列-10,-6,-2,2,…的前多少项的和为54?变式练习解:设题中的等差数列为{an},前n项和为 Sn,由题意可知: a1= -10 d=4 Sn=54
由等差数列前n项和公式可得:
解之得:n=9 , n=-3(舍去)
故等差数列-10,-6,-2,2,…前9项的和为54。
分析:利用公式: 可求得n的值公式应用知三求二 解:由题意 d=20 , n=37 , Sn=629 代入公式得解之得:a1=-343又由公式an=a1+(n-1)d 可求得 an=377答: a1为-343 an为377例 题 大 家 练例2:等差数列-10,-6,-2,2,·······前多少项和是54 ?例1:某长跑运动员7天里每天的训练量(单位:m)是这位长跑运动员7天共跑了多少米?例3 :求集合M={m/m=7n,n N*, m<100}中元素的个数,并求这些元素的和。例1 63000例2 9,(其中-3 舍去)例3 元素个数为14,和为735解:由7n<100, 得 即所以 n 14所以集合中的元素为:这个数列是等差数列, 记为 { an} ,a1=7, a14=98 . 因此,因为 n N* 等差数列的前n项和公式的进一步探究若n+1是偶数时(等差数列的前n项和可能有最大或最小值)已知一个等差数列的前5项和是100,前10项的和是50,则
(1)求其前n项和的公式.
(2)前n项和是否有最大值? 若有,n为何值时取得?最大值是什么?已知等差数列{an},a7=7,则其前13 项的和 S13是多少?牛刀小试(1) 法一:解设此等差数列为{an},首项为a1,公差为d,
前n项和为Sn由已知得,(1)(2)由(1),(2)得因此,已知一个等差数列的前5项和是100,前10项的和是50,(1)求其前n项和的公式.法二:解 设此数列前n项和为 Sn=An2+Bn则由已知得, S5= 25A+5B=100 (1) S10 = 100A+10B=50 (2)由(1),(2)得因此,已知一个等差数列的前5项和是100,前10项的和是50,
(1)求其前n项和的公式.(2)法一:若要使Sn最大,则需即,解之得 n=6此时,(Sn )max= s6 =102法二:利用二次函数求最值课堂小结等差数列前n项和公式在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.公式的推证用的是倒序相加法(关于n的二次函数)
并能运用公式解决简单问题。 情感目标:提高分析和解决问题的能力,
培养创新精神,强化实践能力。独立思考以下问题:问题一: 1+2+3+······+100=?问题二: 1+2+3+······+99=?问题三: 1+2+3+······+n=?等差数列的前n项和德国古代著名数学家高斯9岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?赶快开动脑筋,想一想!1+2+3+···+100=??下面再来看1+2+3+…+98+99+100的高斯算法。设S100=1 + 2 + 3 +…+98+99+100反序S100=100+99+98+…+ 3+ 2+ 1多少个101 ?100个101所以S100=(1+100)×100??首项尾项?总
和?项数 这就是等差数列前n项和的公式!=5050等差数列的前n项和公式的推导由 an=a1+(n-1)d am=an-(n-m)d 得等差数列的前n项和公式的推导等差数列的前n项和公式的其它形式类比梯形面积公式记忆等差数列的前n项和例题1. 根据下列条件,求相应的等差数列 的 根据下列条件,求相应的等差数列 的公式应用选用公式公式应用变用公式 等差数列-10,-6,-2,2,…的前多少项的和为54?变式练习解:设题中的等差数列为{an},前n项和为 Sn,由题意可知: a1= -10 d=4 Sn=54
由等差数列前n项和公式可得:
解之得:n=9 , n=-3(舍去)
故等差数列-10,-6,-2,2,…前9项的和为54。
分析:利用公式: 可求得n的值公式应用知三求二 解:由题意 d=20 , n=37 , Sn=629 代入公式得解之得:a1=-343又由公式an=a1+(n-1)d 可求得 an=377答: a1为-343 an为377例 题 大 家 练例2:等差数列-10,-6,-2,2,·······前多少项和是54 ?例1:某长跑运动员7天里每天的训练量(单位:m)是这位长跑运动员7天共跑了多少米?例3 :求集合M={m/m=7n,n N*, m<100}中元素的个数,并求这些元素的和。例1 63000例2 9,(其中-3 舍去)例3 元素个数为14,和为735解:由7n<100, 得 即所以 n 14所以集合中的元素为:这个数列是等差数列, 记为 { an} ,a1=7, a14=98 . 因此,因为 n N* 等差数列的前n项和公式的进一步探究若n+1是偶数时(等差数列的前n项和可能有最大或最小值)已知一个等差数列的前5项和是100,前10项的和是50,则
(1)求其前n项和的公式.
(2)前n项和是否有最大值? 若有,n为何值时取得?最大值是什么?已知等差数列{an},a7=7,则其前13 项的和 S13是多少?牛刀小试(1) 法一:解设此等差数列为{an},首项为a1,公差为d,
前n项和为Sn由已知得,(1)(2)由(1),(2)得因此,已知一个等差数列的前5项和是100,前10项的和是50,(1)求其前n项和的公式.法二:解 设此数列前n项和为 Sn=An2+Bn则由已知得, S5= 25A+5B=100 (1) S10 = 100A+10B=50 (2)由(1),(2)得因此,已知一个等差数列的前5项和是100,前10项的和是50,
(1)求其前n项和的公式.(2)法一:若要使Sn最大,则需即,解之得 n=6此时,(Sn )max= s6 =102法二:利用二次函数求最值课堂小结等差数列前n项和公式在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.公式的推证用的是倒序相加法(关于n的二次函数)
