华师版数学八年级上册 13.2三角形全等的判定第2课时边角边 课件(共18张PPT)
文档属性
| 名称 | 华师版数学八年级上册 13.2三角形全等的判定第2课时边角边 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 582.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 20:30:03 | ||
图片预览




文档简介
(共18张PPT)
13.2 三角形全等的判定
第2课时 边角边
学习目标
探索并掌握基本事实:两边及其夹角分别相等的两个三角形全等;
能利用基本事实“边角边”判定两个三角形全等或进行相关计算,解决一些实际问题,提高推理论证及运算能力.
在上节课的学习中,我们知道了仅有一组或两组对应元素相等无法判定两个三角形全等.
还记得上节课的课后思考题吗:如果有三组元
素对应相等,能判定两个三角形全等吗?
三组元素对应相等有几种可能?
温故知新
三角形有六个元素:三条边、三个角.
选取三组对应元素相等,可能出现的情况:
两边一角对应相等;
两角一边对应相等;
三条边对应相等;
三个角对应相等.
?
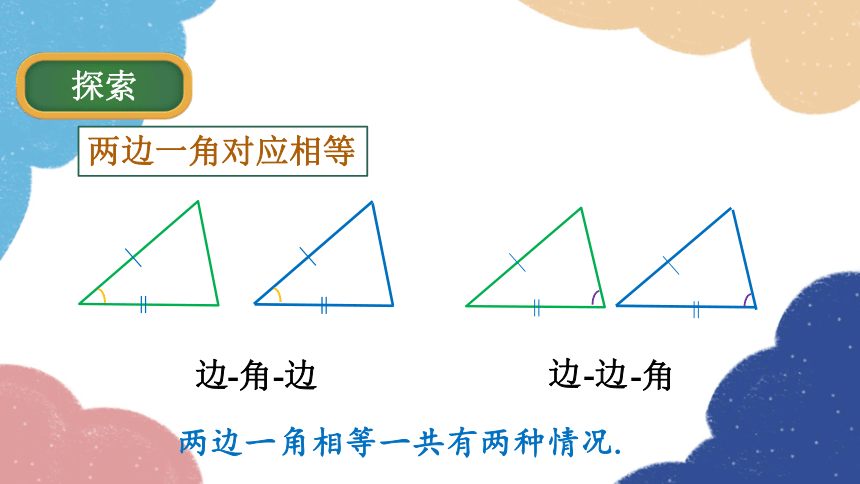
两边一角对应相等
探索
边
边
两边一角相等一共有两种情况.
-角
-边
-角
-边
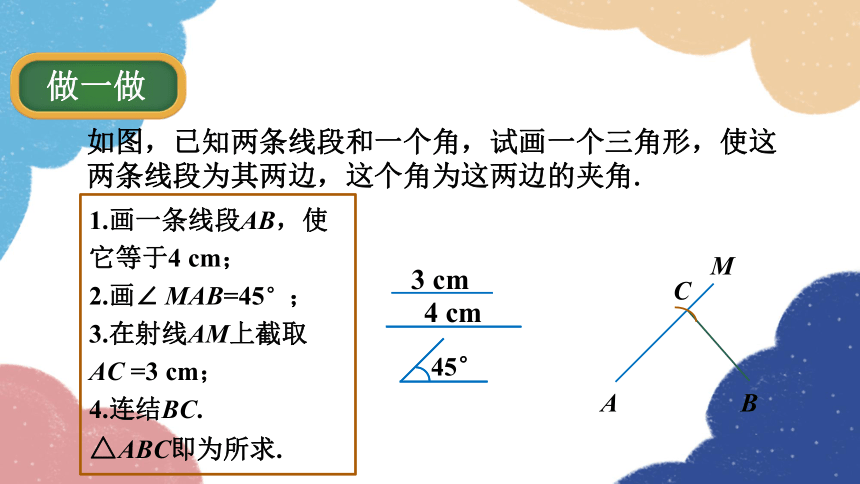
做一做
如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.
45°
3 cm
4 cm
1.画一条线段AB,使它等于4 cm;
2.画∠ MAB=45°;
3.在射线AM上截取
AC =3 cm;
4.连结BC.
△ABC即为所求.
A
B
M
C
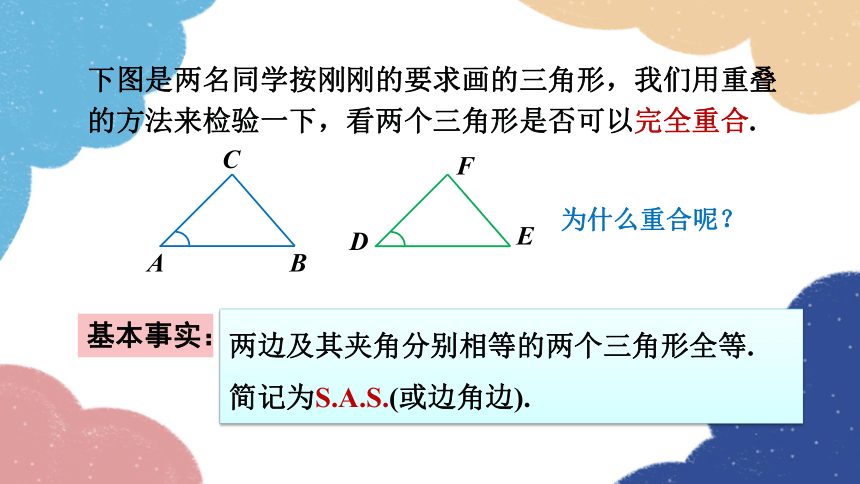
下图是两名同学按刚刚的要求画的三角形,我们用重叠的方法来检验一下,看两个三角形是否可以完全重合.
基本事实:
A
B
C
D
E
F
两边及其夹角分别相等的两个三角形全等.
简记为S.A.S.(或边角边).
为什么重合呢?
例题
【例1】如图,已知线段AC、BD相交于点E,AE = DE,BE = CE. 求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
∵AE=DE(已知),
∠AEB= ∠DEC (对顶角相等),
BE=CE(已知),
∴△ABE≌△DCE(S.A.S.).
总结
应用S.A.S.判定两个三角形全等的“三注意”:
1.注意位置:角的位置在图形中两边之间;
2.注意书写:角写在两边之间;
3.注意隐含条件:如图形中的公共边、公共角、
对顶角等.
例题
【例2】如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达点A 和点B的点C,连结AC并延长到D,使CD =CA,连结BC 并延长到E,使CE =CB,连结ED,那么量出DE的长就是A、B的距离.你知道其中的道理吗?
我们先把它抽象为数学语言.
A
B
C
D
E
1
2
已知:AD与BE相交于点C,CA=CD,CB=CE.
求证:AB=DE.
∵AC = DC(已知),
∠1 =∠2 (对顶角相等),
BC =EC(已知) ,
证明:在△ABC 和△DEC 中,
∴△ABC ≌△DEC(S.A.S.).
∴AB =DE (全等三角形的对应边相等).
A
B
C
D
E
1
2
在实际生活中,对于难以实地测量的距离,常常通过构造两个全等三角形,将需要测量的距离转化到容易测量的边或者已知边上来,进而求解.
探索
“两边及夹角”对应相等可以判定两个三角形全等,那么“两边及邻角”可以判定两个三角形全等吗?
如图,在墙上找一水平线AB,将一根长木条AC固定,一根短木条一端固定,另一端刚刚落在
水平线AB上时固定,
则有两种相交情况:
B点和D点.
B
C
D
A
在△ADC和△ABC中,
AC=AC,
CD=CB,
∠A=∠A,
满足“边边角”,
但两个三角形不全等.
“两边及夹角”对应相等可以判定两个三角形全等,那么“两边及邻角”可以判定两个三角形全等吗?
A
B
C
D
“边边角”不能判定两个三角形全等.
练习
1.如图,a,b,c 分别是△ABC 的三边长,则下面与△ABC 一定全等的三角形是( )
B
2.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量 AB=9 cm,则容器的内径A′B′为______cm.
9
3.小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,问:EH=FH吗
E
F
D
H
解: EH=FH.理由如下:
∵在△DEH和△DFH中,
ED=FD (已知),
∠EDH=∠FDH(已知),
DH=DH(公共边),
∴ △DEH≌△DFH(S.A.S.).
∴ EH=FH(全等三角形的对应边相等).
1.“边角边” 基本事实:
2.“边角边”判定三角形全等的应用.
3.“边边角”_____ 作为判定两个三角形全等的依据 .
两边及其夹角分别相等的两个三角形全等.
简记为S.A.S.(或边角边).
不能
课堂小结
13.2 三角形全等的判定
第2课时 边角边
学习目标
探索并掌握基本事实:两边及其夹角分别相等的两个三角形全等;
能利用基本事实“边角边”判定两个三角形全等或进行相关计算,解决一些实际问题,提高推理论证及运算能力.
在上节课的学习中,我们知道了仅有一组或两组对应元素相等无法判定两个三角形全等.
还记得上节课的课后思考题吗:如果有三组元
素对应相等,能判定两个三角形全等吗?
三组元素对应相等有几种可能?
温故知新
三角形有六个元素:三条边、三个角.
选取三组对应元素相等,可能出现的情况:
两边一角对应相等;
两角一边对应相等;
三条边对应相等;
三个角对应相等.
?
两边一角对应相等
探索
边
边
两边一角相等一共有两种情况.
-角
-边
-角
-边
做一做
如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.
45°
3 cm
4 cm
1.画一条线段AB,使它等于4 cm;
2.画∠ MAB=45°;
3.在射线AM上截取
AC =3 cm;
4.连结BC.
△ABC即为所求.
A
B
M
C
下图是两名同学按刚刚的要求画的三角形,我们用重叠的方法来检验一下,看两个三角形是否可以完全重合.
基本事实:
A
B
C
D
E
F
两边及其夹角分别相等的两个三角形全等.
简记为S.A.S.(或边角边).
为什么重合呢?
例题
【例1】如图,已知线段AC、BD相交于点E,AE = DE,BE = CE. 求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
∵AE=DE(已知),
∠AEB= ∠DEC (对顶角相等),
BE=CE(已知),
∴△ABE≌△DCE(S.A.S.).
总结
应用S.A.S.判定两个三角形全等的“三注意”:
1.注意位置:角的位置在图形中两边之间;
2.注意书写:角写在两边之间;
3.注意隐含条件:如图形中的公共边、公共角、
对顶角等.
例题
【例2】如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达点A 和点B的点C,连结AC并延长到D,使CD =CA,连结BC 并延长到E,使CE =CB,连结ED,那么量出DE的长就是A、B的距离.你知道其中的道理吗?
我们先把它抽象为数学语言.
A
B
C
D
E
1
2
已知:AD与BE相交于点C,CA=CD,CB=CE.
求证:AB=DE.
∵AC = DC(已知),
∠1 =∠2 (对顶角相等),
BC =EC(已知) ,
证明:在△ABC 和△DEC 中,
∴△ABC ≌△DEC(S.A.S.).
∴AB =DE (全等三角形的对应边相等).
A
B
C
D
E
1
2
在实际生活中,对于难以实地测量的距离,常常通过构造两个全等三角形,将需要测量的距离转化到容易测量的边或者已知边上来,进而求解.
探索
“两边及夹角”对应相等可以判定两个三角形全等,那么“两边及邻角”可以判定两个三角形全等吗?
如图,在墙上找一水平线AB,将一根长木条AC固定,一根短木条一端固定,另一端刚刚落在
水平线AB上时固定,
则有两种相交情况:
B点和D点.
B
C
D
A
在△ADC和△ABC中,
AC=AC,
CD=CB,
∠A=∠A,
满足“边边角”,
但两个三角形不全等.
“两边及夹角”对应相等可以判定两个三角形全等,那么“两边及邻角”可以判定两个三角形全等吗?
A
B
C
D
“边边角”不能判定两个三角形全等.
练习
1.如图,a,b,c 分别是△ABC 的三边长,则下面与△ABC 一定全等的三角形是( )
B
2.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量 AB=9 cm,则容器的内径A′B′为______cm.
9
3.小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,问:EH=FH吗
E
F
D
H
解: EH=FH.理由如下:
∵在△DEH和△DFH中,
ED=FD (已知),
∠EDH=∠FDH(已知),
DH=DH(公共边),
∴ △DEH≌△DFH(S.A.S.).
∴ EH=FH(全等三角形的对应边相等).
1.“边角边” 基本事实:
2.“边角边”判定三角形全等的应用.
3.“边边角”_____ 作为判定两个三角形全等的依据 .
两边及其夹角分别相等的两个三角形全等.
简记为S.A.S.(或边角边).
不能
课堂小结
