人教版数学八年级上册 13.3等腰三角形第2课时等边三角形课件 20张PPT
文档属性
| 名称 | 人教版数学八年级上册 13.3等腰三角形第2课时等边三角形课件 20张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 20:47:52 | ||
图片预览



文档简介
(共20张PPT)
13.3 等腰三角形
第2课时 等边三角形
1.理解并掌握等边三角形的定义,探索等边三角形的性质和判定方法.
2.能够用等边三角形的知识解决相应的数学问题.
3.理解含30°角的直角三角形的性质,并会应用它进行有关的证明和计算.
学习目标
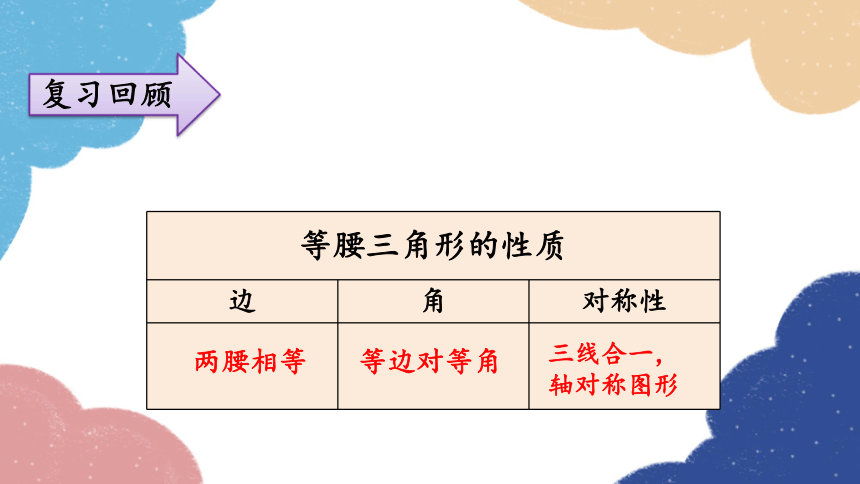
复习回顾
等腰三角形的性质
边 角 对称性
两腰相等
等边对等角
三线合一,
轴对称图形
新课引入
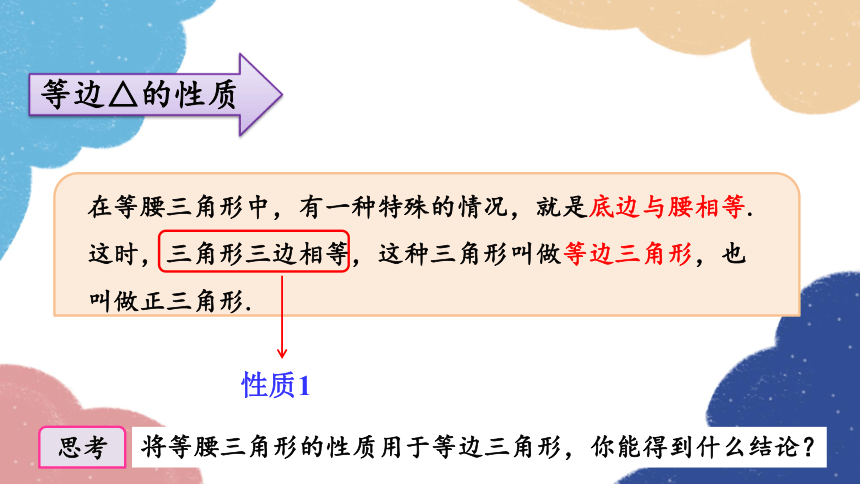
在等腰三角形中,有一种特殊的情况,就是底边与腰相等.这时,三角形三边相等,这种三角形叫做等边三角形,也叫做正三角形.
在等腰三角形中,有一种特殊的情况,就是底边与腰相等.这时,三角形三边相等,这种三角形叫做等边三角形,也叫做正三角形.
将等腰三角形的性质用于等边三角形,你能得到什么结论?
思考
等边△的性质
性质1
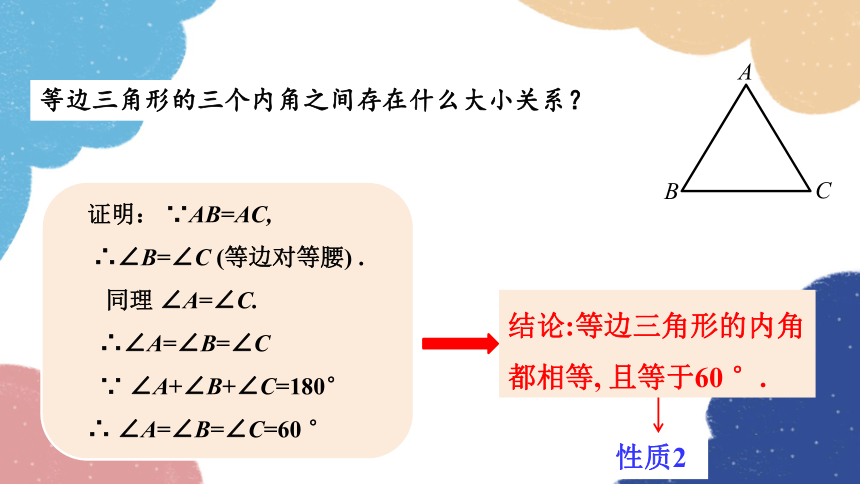
等边三角形的三个内角之间存在什么大小关系?
A
B
C
证明: ∵AB=AC,
∴∠B=∠C (等边对等腰) .
同理 ∠A=∠C.
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60 °
结论:等边三角形的内角
都相等, 且等于60 °.
性质2
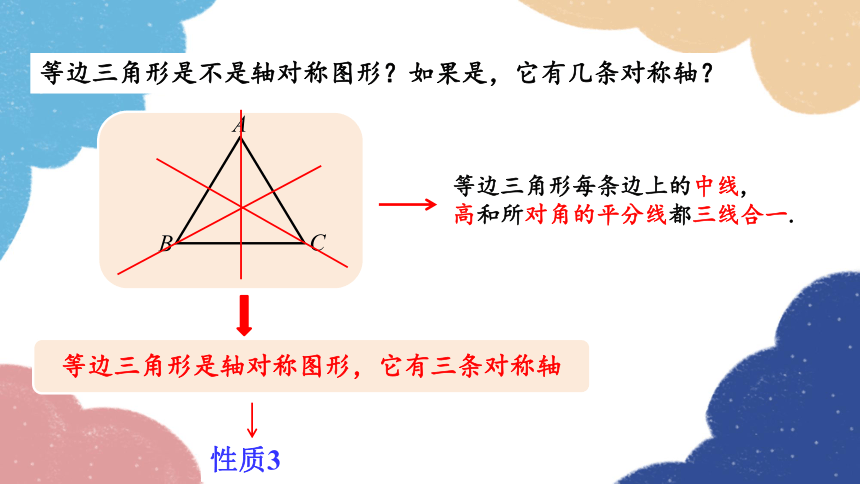
等边三角形是不是轴对称图形?如果是,它有几条对称轴?
A
B
C
等边三角形是轴对称图形,它有三条对称轴
性质3
等边三角形每条边上的中线,
高和所对角的平分线都三线合一.
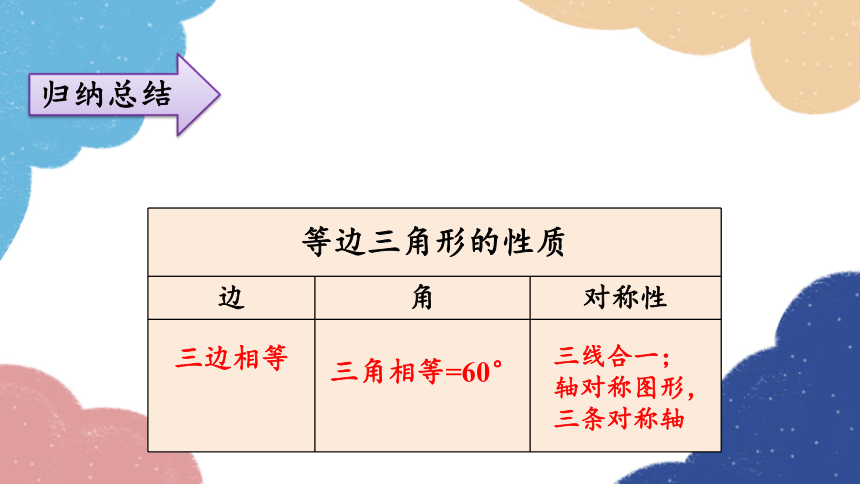
归纳总结
等边三角形的性质
边 角 对称性
三边相等
三角相等=60°
三线合一;
轴对称图形,三条对称轴
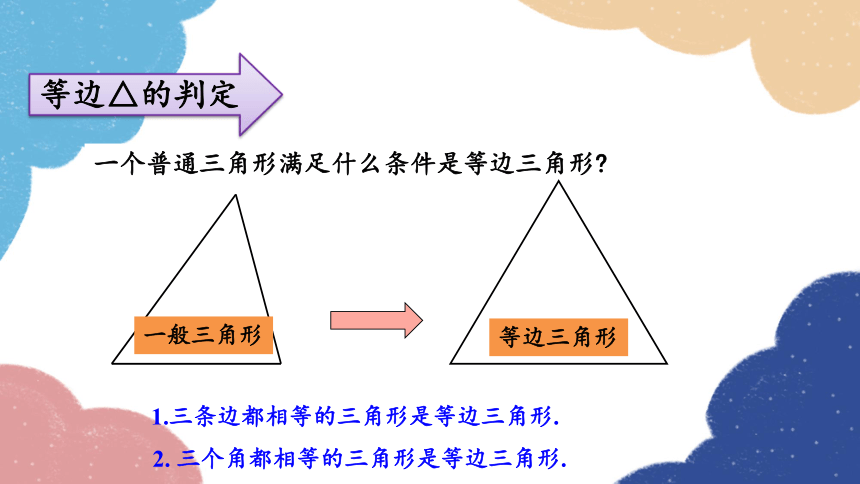
等边△的判定
一个普通三角形满足什么条件是等边三角形
一般三角形
1.三条边都相等的三角形是等边三角形.
2. 三个角都相等的三角形是等边三角形.
等边三角形
3.有一个角是60°的等腰三角形是等边三角形.
等腰三角形
等边三角形
等腰三角形满足什么条件时是等边三角形
例1:如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E.证明:△ACE是等边三角形.
典例讲解
分析:利用平行线的性质以及平角的定义求出△ACE的每一个内角都是60°.
例1:如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E.证明:△ACE是等边三角形.
典例讲解
含30°角的Rt△
等边三角形是轴对称图形,若沿着其中一条对称轴折叠,能产生什么特殊图形?
产生了一个特殊的直角三角形
其中一个锐角=30°
含30°角的直角 △ABC 的直角边BC 与斜边AB 之间有什么
数量关系?
D
A
B
C
30°
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
含30°角的Rt三角形的性质
符号语言:
典例讲解
例2:已知:等腰三角形的底角为15°,腰长为2a. 求:腰上的高.
D
15°
A
C
B
15°
2a
随堂训练
1.如图所示,在等边△ABC中,AB=3,∠ABC、∠ACB的平分线相交于点O,过O作OE∥AB,OF∥AC,交BC于点E、F,则△OEF的周长为 .
【解析】由于OB平分∠ABC,OE∥AB,可以得出OE=BE.同理可以得出OF=FC,因此△OEF的周长=OE+EF+OF=BE+EF+FC=BC=AB=3.
3
2.如图,在等边△ABC中,点D是BC边的中点,以AD为边作
等边△ADE,则∠CAE= .
【解析】点D是等边△ABC中BC边的中点,故∠DAC=30°;
在等边△ADE中,∠CAE=60°-30°=30°.
答案:30°
30°
3.如图,△ABC 是等边三角形,若点D、E 在边AB、AC 的反向
延长线上,且DE∥BC,求证:△ADE 是等边三角形.
证明 ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
4.如图,D,E,F分别是等边△ABC三边上的点,且AD=BE=CF,
求证:△DEF是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°, AB=BC=CA.
∵AD=BE=CF, ∴AF=BD=CE.
∴△ADF≌△BED≌△CFE.
∴DF=ED=FE.
∴△DEF是等边三角形.
13.3 等腰三角形
第2课时 等边三角形
1.理解并掌握等边三角形的定义,探索等边三角形的性质和判定方法.
2.能够用等边三角形的知识解决相应的数学问题.
3.理解含30°角的直角三角形的性质,并会应用它进行有关的证明和计算.
学习目标
复习回顾
等腰三角形的性质
边 角 对称性
两腰相等
等边对等角
三线合一,
轴对称图形
新课引入
在等腰三角形中,有一种特殊的情况,就是底边与腰相等.这时,三角形三边相等,这种三角形叫做等边三角形,也叫做正三角形.
在等腰三角形中,有一种特殊的情况,就是底边与腰相等.这时,三角形三边相等,这种三角形叫做等边三角形,也叫做正三角形.
将等腰三角形的性质用于等边三角形,你能得到什么结论?
思考
等边△的性质
性质1
等边三角形的三个内角之间存在什么大小关系?
A
B
C
证明: ∵AB=AC,
∴∠B=∠C (等边对等腰) .
同理 ∠A=∠C.
∴∠A=∠B=∠C
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60 °
结论:等边三角形的内角
都相等, 且等于60 °.
性质2
等边三角形是不是轴对称图形?如果是,它有几条对称轴?
A
B
C
等边三角形是轴对称图形,它有三条对称轴
性质3
等边三角形每条边上的中线,
高和所对角的平分线都三线合一.
归纳总结
等边三角形的性质
边 角 对称性
三边相等
三角相等=60°
三线合一;
轴对称图形,三条对称轴
等边△的判定
一个普通三角形满足什么条件是等边三角形
一般三角形
1.三条边都相等的三角形是等边三角形.
2. 三个角都相等的三角形是等边三角形.
等边三角形
3.有一个角是60°的等腰三角形是等边三角形.
等腰三角形
等边三角形
等腰三角形满足什么条件时是等边三角形
例1:如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E.证明:△ACE是等边三角形.
典例讲解
分析:利用平行线的性质以及平角的定义求出△ACE的每一个内角都是60°.
例1:如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E.证明:△ACE是等边三角形.
典例讲解
含30°角的Rt△
等边三角形是轴对称图形,若沿着其中一条对称轴折叠,能产生什么特殊图形?
产生了一个特殊的直角三角形
其中一个锐角=30°
含30°角的直角 △ABC 的直角边BC 与斜边AB 之间有什么
数量关系?
D
A
B
C
30°
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
含30°角的Rt三角形的性质
符号语言:
典例讲解
例2:已知:等腰三角形的底角为15°,腰长为2a. 求:腰上的高.
D
15°
A
C
B
15°
2a
随堂训练
1.如图所示,在等边△ABC中,AB=3,∠ABC、∠ACB的平分线相交于点O,过O作OE∥AB,OF∥AC,交BC于点E、F,则△OEF的周长为 .
【解析】由于OB平分∠ABC,OE∥AB,可以得出OE=BE.同理可以得出OF=FC,因此△OEF的周长=OE+EF+OF=BE+EF+FC=BC=AB=3.
3
2.如图,在等边△ABC中,点D是BC边的中点,以AD为边作
等边△ADE,则∠CAE= .
【解析】点D是等边△ABC中BC边的中点,故∠DAC=30°;
在等边△ADE中,∠CAE=60°-30°=30°.
答案:30°
30°
3.如图,△ABC 是等边三角形,若点D、E 在边AB、AC 的反向
延长线上,且DE∥BC,求证:△ADE 是等边三角形.
证明 ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
4.如图,D,E,F分别是等边△ABC三边上的点,且AD=BE=CF,
求证:△DEF是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°, AB=BC=CA.
∵AD=BE=CF, ∴AF=BD=CE.
∴△ADF≌△BED≌△CFE.
∴DF=ED=FE.
∴△DEF是等边三角形.
