2023-2024学年人教版八年级数学下册 19.1.1 求一次函数的解析式 11张PPT
文档属性
| 名称 | 2023-2024学年人教版八年级数学下册 19.1.1 求一次函数的解析式 11张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 604.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 20:55:58 | ||
图片预览




文档简介
(共11张PPT)
第十九章 一次函数
第1课时 求一次函数的解析式
2、一次函数的解析式:
y=kx+b
(k,b为常数,k≠0)
1、正比例函数的解析式:
y=kx
(k为常数且k≠0)
复习巩固
3、已知一次函数y=kx+2,当x=5时y的值为4,则k的值是______.
0.4
5、若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点
( )
A.(-1,1) B.(2,2) C.(-2,2) D.(2,一2)
B
4、若直线y=kx+b平行直线y=-3x+2,且与y轴交点的纵坐标为-5,则k= ,b= 。
-3
-5
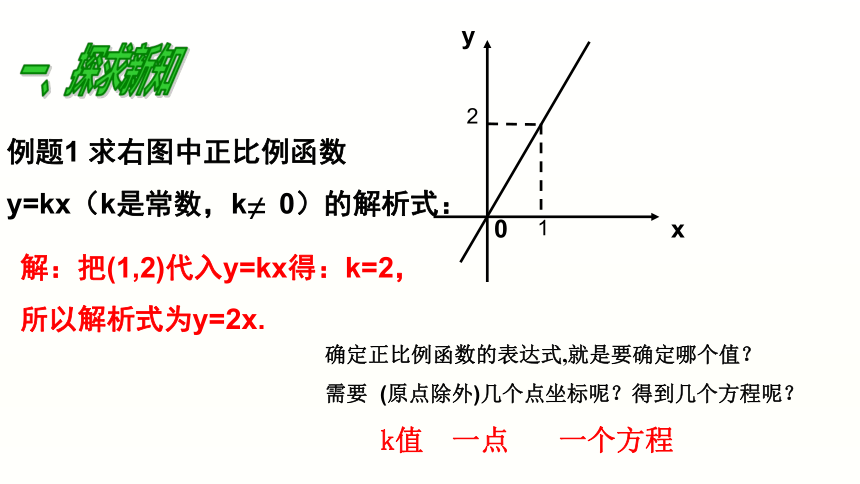
解:把(1,2)代入y=kx得:k=2,
所以解析式为y=2x.
例题1 求右图中正比例函数
y=kx(k是常数,k 0)的解析式:
一、探求新知
1
2
x
y
0
确定正比例函数的表达式,就是要确定哪个值?
需要 (原点除外)几个点坐标呢?得到几个方程呢?
k值
一点
一个方程
例2. 如图,已知直线y=kx+b经过点A,点B.
求直线的解析式;
解:(1)将点A(-3,3),点B(0,-3)
代入y=kx+b,得
解得
∴直线的解析式为y=-2x-3.
确定一次函数的表达式,需要确定哪些值?
需要几个点坐标呢?得到几个方程呢?
k、b值
两点
二个方程
想一想
确定正比例函数的表达式,就是要确定哪个值?需要 (原点除外)几个点坐标呢?得到几个方程呢?
总结:在确定函数表达式时,要求几个系数,就需要知道几个点的坐标。进而得到所需的方程或方程组。
一次函数呢?
k值
一点
k、b值
两点
一个方程
二个方程
例3、已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式y=kx+b( )
将(3,5)与(-4,-9)代入y=kx+b,得
5=3k+b
-9 =-4k+b
解得 k=2
b=-1
∴这个一次函数的解析式为y=2x-1
设
代
解
待定系数法
写
探究新知
利用点的坐标求函数关系式
先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法。
用待定系数法解题一般分为几步?
一设、二代、三解、四写:
1. 设一次函数的一般形式y=kx+b(k≠0);
2. 根据已知条件列出关于k、b的二元一次方程组;
3. 解这个方程组,求出k、b;
4. 将已经求出的 k、b的值代入解析式,写出解析式.
形成概念
例4
x ... -2 -1 0 1 2 ...
y ... -3 -1 1 3 5 ...
例5 直线 与直线y=-2x-1平行且过点(1,3),求直线 的解析式.
已知一点和其他条件求一次函数解析式
解:∵直线 与直线y=-2x-1平行,
∴可设直线 的解析式为y=-2x+b.
又∵直线 过点(1,3),
∴3=-2×1+b. 解得b=5.
∴直线 的解析式为y=-2x+5.
能力提升
例6 . 已知y=y1-2y2,其中y1与x成正比例,y2与x+1成正比例,且当x=1时,y=3;当x=2时,y=5.
(1)求y与x的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
解:(1)设y1=k1x(k1≠0),y2=k2(x+1)(k2≠0),
则y=k1x-2k2(x+1).
根据题意,得解得
∴y=x-2×(-)×(x+1)=2x+1.
(2)把x=a,y=3代入y=2x+1,得2a+1=3.
解得a=1.
能力提升
小结
求函数关系式的一般步骤
可归纳为:“一设、二代、三解、四写”
1. 设一次函数的一般形式y=kx+b(k≠0);
2. 根据已知条件列出关于k、b的二元一次方程组;
3. 解这个方程组,求出k、b;
4. 将已经求出的 k、b的值代入解析式.
第十九章 一次函数
第1课时 求一次函数的解析式
2、一次函数的解析式:
y=kx+b
(k,b为常数,k≠0)
1、正比例函数的解析式:
y=kx
(k为常数且k≠0)
复习巩固
3、已知一次函数y=kx+2,当x=5时y的值为4,则k的值是______.
0.4
5、若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点
( )
A.(-1,1) B.(2,2) C.(-2,2) D.(2,一2)
B
4、若直线y=kx+b平行直线y=-3x+2,且与y轴交点的纵坐标为-5,则k= ,b= 。
-3
-5
解:把(1,2)代入y=kx得:k=2,
所以解析式为y=2x.
例题1 求右图中正比例函数
y=kx(k是常数,k 0)的解析式:
一、探求新知
1
2
x
y
0
确定正比例函数的表达式,就是要确定哪个值?
需要 (原点除外)几个点坐标呢?得到几个方程呢?
k值
一点
一个方程
例2. 如图,已知直线y=kx+b经过点A,点B.
求直线的解析式;
解:(1)将点A(-3,3),点B(0,-3)
代入y=kx+b,得
解得
∴直线的解析式为y=-2x-3.
确定一次函数的表达式,需要确定哪些值?
需要几个点坐标呢?得到几个方程呢?
k、b值
两点
二个方程
想一想
确定正比例函数的表达式,就是要确定哪个值?需要 (原点除外)几个点坐标呢?得到几个方程呢?
总结:在确定函数表达式时,要求几个系数,就需要知道几个点的坐标。进而得到所需的方程或方程组。
一次函数呢?
k值
一点
k、b值
两点
一个方程
二个方程
例3、已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式y=kx+b( )
将(3,5)与(-4,-9)代入y=kx+b,得
5=3k+b
-9 =-4k+b
解得 k=2
b=-1
∴这个一次函数的解析式为y=2x-1
设
代
解
待定系数法
写
探究新知
利用点的坐标求函数关系式
先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法。
用待定系数法解题一般分为几步?
一设、二代、三解、四写:
1. 设一次函数的一般形式y=kx+b(k≠0);
2. 根据已知条件列出关于k、b的二元一次方程组;
3. 解这个方程组,求出k、b;
4. 将已经求出的 k、b的值代入解析式,写出解析式.
形成概念
例4
x ... -2 -1 0 1 2 ...
y ... -3 -1 1 3 5 ...
例5 直线 与直线y=-2x-1平行且过点(1,3),求直线 的解析式.
已知一点和其他条件求一次函数解析式
解:∵直线 与直线y=-2x-1平行,
∴可设直线 的解析式为y=-2x+b.
又∵直线 过点(1,3),
∴3=-2×1+b. 解得b=5.
∴直线 的解析式为y=-2x+5.
能力提升
例6 . 已知y=y1-2y2,其中y1与x成正比例,y2与x+1成正比例,且当x=1时,y=3;当x=2时,y=5.
(1)求y与x的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
解:(1)设y1=k1x(k1≠0),y2=k2(x+1)(k2≠0),
则y=k1x-2k2(x+1).
根据题意,得解得
∴y=x-2×(-)×(x+1)=2x+1.
(2)把x=a,y=3代入y=2x+1,得2a+1=3.
解得a=1.
能力提升
小结
求函数关系式的一般步骤
可归纳为:“一设、二代、三解、四写”
1. 设一次函数的一般形式y=kx+b(k≠0);
2. 根据已知条件列出关于k、b的二元一次方程组;
3. 解这个方程组,求出k、b;
4. 将已经求出的 k、b的值代入解析式.
