高中数学人教A版2019必修第一册 2.1等式性质与不等式性质(第2课时) 教案(表格式)(含答案)
文档属性
| 名称 | 高中数学人教A版2019必修第一册 2.1等式性质与不等式性质(第2课时) 教案(表格式)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 669.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 15:48:53 | ||
图片预览


文档简介
教学单元 第二章 一元二次函数、方程和不等式 教学内容 2.1等式性质与不等式性质(第2课时)
教学目标
学习目标 1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题; 2. 进一步掌握作差、作商、综合法等比较法比较实数的大小; 3. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质. 核心素养 1. 掌握等式性质与不等式性质以及推论,培养学生数学抽象的核心素养; 2. 进一步掌握作差比较法比较实数的大小,提升数学运算的核心素养; 3. 能利用不等式的性质证明简单的不等式、求代数式的取值范围,强化逻辑推理的核心素养。
教学重难点
重点:掌握不等式性质及其应用. 难点:类比等式的基本性质及其蕴含的思想方法,研究不等式的基本性质;等式与不等式的共性与差异.
学情分析
学生在小学和初中阶段已经接触过不等式,但上升到理论层次,例如比较大小的理论根据--作差法,对不等式性质的推导与证明,利用不等式性质解决简单的证明等问题,还有一定的难度,所以在教学过程中,注意引导学生分析不等式个性质的条件及结论,做到有理有据、严谨细致、条例清楚,提高逻辑推理和数学运算的核心素养。
教学过程
教学环节 教师活动 学生活动 设计意图
情境导入 上一课时我们学习了比较两个数的大小,为我们学习不等式的性质奠定了基础. 让我们先回顾等式的有关性质: 性质1 如果那么(对称性) 性质2 如果那么(传递性) 性质3 如果那么 性质4 如果那么 性质5 如果那么 学生回忆所学知识 通过引导学生回忆,帮助学生用数学式子表示出来,提高学生用数学抽象的思维方式思考并解决问题的能力
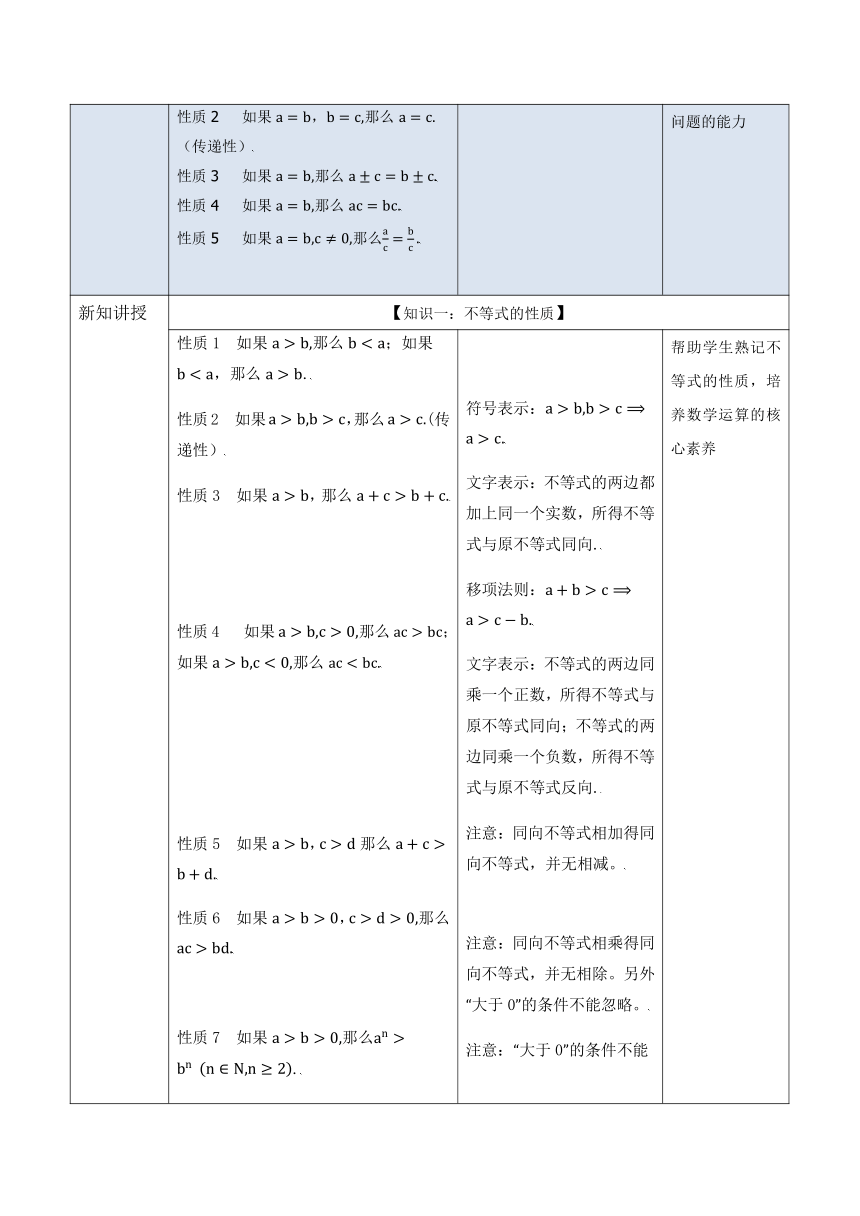
新知讲授 【知识一:不等式的性质】
性质1 如果如果,那么. 性质2 如果,那么(传递性) 性质3 如果,那么 性质4 如果那么; 如果那么 性质5 如果,那么 性质6 如果,那么 性质7 如果那么. 重要结论:如果,那么,如果那么. 符号表示: 文字表示:不等式的两边都加上同一个实数,所得不等式与原不等式同向. 移项法则: 文字表示:不等式的两边同乘一个正数,所得不等式与原不等式同向;不等式的两边同乘一个负数,所得不等式与原不等式反向. 注意:同向不等式相加得同向不等式,并无相减。 注意:同向不等式相乘得同向不等式,并无相除。另外“大于0”的条件不能忽略。 注意:“大于0”的条件不能忽略。 帮助学生熟记不等式的性质,培养数学运算的核心素养
例1.下列结论: ①若,则; ②若,则; ③若,则; ④若,则. 其中正确结论的序号是 . 利用不等式性质判断不等式是否成立的方法: (1)运用不等式的性质判断:要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质; (2)特殊值法:取特殊值时,要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算。尤其是在选择题中经常采用这种方法。 答案:④ 通过例题,使学生熟记不等式的性质,培养数学运算的核心素养
【知识二:根据不等式的性质证明不等式】
例2.已知a>b>0,c<0,求证: 证明:∵ ∴ 于是, 即 由得 利用不等式的性质证明不等 式注意事项 (1)利用不等式的性质及其推论可以证明一些不等式.解决此类问题一定要在理解的基础上,记准、记熟不等式的性质并注意在解题中灵活准确地加以应用. (2)应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则. 通过不等式的判断、证明,使学生熟练掌握不等式的性质,培养学生解决问题的能力。
【知识三:根据不等式的性质求取值范围】
例3.已知-≤α<β≤,求,的范围. ∵-≤α<β≤, ∴-≤<,-<≤.两式相加,得-<<. ∵-<≤,∴-≤-<,∴-≤<. 又∵α<β,∴<0.∴-≤<0. 利用不等式的性质求取值范围时,应注意: 同向不等式具有可加性与可乘性(同正),但是不具有可减性与可除性,应用时要充分利用所给条件进行适当变形来求取值范围,注意变形的等价性。 通过例题,使学生熟记不等式的性质,灵活灵活不等式的性质解决问题,培养数学运算的核心素养
课堂练习 1.用不等号“”或“”填空: (1)如果,,那么 ; (2)如果,,那么 ; (3)如果,那么 ; (4)如果,那么 ; 2.已知实数满足,,求的取值范围 3.已知1课堂小结 1.利用不等式的性质判断命题的真假时, 一定要注意不等式成立的条件.不要弱化 条件,尤其是不能凭空捏造性质. 2.利用不等式的性质证明简单的不等式 是否成立,实际上就是根据不等式的性质 把不等式进行适当的变形,证明过程中注 意不等式成立的条件. 通过总结,让学生进一步巩固不等式的性质,辨析不等式成立的条件,树立用不等式解决相关问题的意识。
板书设计 1.等式性质 2.不等式性质 例1 例2 例3. 练习
课后作业 完成作业。 完成课后作用,巩固回忆知识。
教学目标
学习目标 1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题; 2. 进一步掌握作差、作商、综合法等比较法比较实数的大小; 3. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质. 核心素养 1. 掌握等式性质与不等式性质以及推论,培养学生数学抽象的核心素养; 2. 进一步掌握作差比较法比较实数的大小,提升数学运算的核心素养; 3. 能利用不等式的性质证明简单的不等式、求代数式的取值范围,强化逻辑推理的核心素养。
教学重难点
重点:掌握不等式性质及其应用. 难点:类比等式的基本性质及其蕴含的思想方法,研究不等式的基本性质;等式与不等式的共性与差异.
学情分析
学生在小学和初中阶段已经接触过不等式,但上升到理论层次,例如比较大小的理论根据--作差法,对不等式性质的推导与证明,利用不等式性质解决简单的证明等问题,还有一定的难度,所以在教学过程中,注意引导学生分析不等式个性质的条件及结论,做到有理有据、严谨细致、条例清楚,提高逻辑推理和数学运算的核心素养。
教学过程
教学环节 教师活动 学生活动 设计意图
情境导入 上一课时我们学习了比较两个数的大小,为我们学习不等式的性质奠定了基础. 让我们先回顾等式的有关性质: 性质1 如果那么(对称性) 性质2 如果那么(传递性) 性质3 如果那么 性质4 如果那么 性质5 如果那么 学生回忆所学知识 通过引导学生回忆,帮助学生用数学式子表示出来,提高学生用数学抽象的思维方式思考并解决问题的能力
新知讲授 【知识一:不等式的性质】
性质1 如果如果,那么. 性质2 如果,那么(传递性) 性质3 如果,那么 性质4 如果那么; 如果那么 性质5 如果,那么 性质6 如果,那么 性质7 如果那么. 重要结论:如果,那么,如果那么. 符号表示: 文字表示:不等式的两边都加上同一个实数,所得不等式与原不等式同向. 移项法则: 文字表示:不等式的两边同乘一个正数,所得不等式与原不等式同向;不等式的两边同乘一个负数,所得不等式与原不等式反向. 注意:同向不等式相加得同向不等式,并无相减。 注意:同向不等式相乘得同向不等式,并无相除。另外“大于0”的条件不能忽略。 注意:“大于0”的条件不能忽略。 帮助学生熟记不等式的性质,培养数学运算的核心素养
例1.下列结论: ①若,则; ②若,则; ③若,则; ④若,则. 其中正确结论的序号是 . 利用不等式性质判断不等式是否成立的方法: (1)运用不等式的性质判断:要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质; (2)特殊值法:取特殊值时,要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算。尤其是在选择题中经常采用这种方法。 答案:④ 通过例题,使学生熟记不等式的性质,培养数学运算的核心素养
【知识二:根据不等式的性质证明不等式】
例2.已知a>b>0,c<0,求证: 证明:∵ ∴ 于是, 即 由得 利用不等式的性质证明不等 式注意事项 (1)利用不等式的性质及其推论可以证明一些不等式.解决此类问题一定要在理解的基础上,记准、记熟不等式的性质并注意在解题中灵活准确地加以应用. (2)应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则. 通过不等式的判断、证明,使学生熟练掌握不等式的性质,培养学生解决问题的能力。
【知识三:根据不等式的性质求取值范围】
例3.已知-≤α<β≤,求,的范围. ∵-≤α<β≤, ∴-≤<,-<≤.两式相加,得-<<. ∵-<≤,∴-≤-<,∴-≤<. 又∵α<β,∴<0.∴-≤<0. 利用不等式的性质求取值范围时,应注意: 同向不等式具有可加性与可乘性(同正),但是不具有可减性与可除性,应用时要充分利用所给条件进行适当变形来求取值范围,注意变形的等价性。 通过例题,使学生熟记不等式的性质,灵活灵活不等式的性质解决问题,培养数学运算的核心素养
课堂练习 1.用不等号“”或“”填空: (1)如果,,那么 ; (2)如果,,那么 ; (3)如果,那么 ; (4)如果,那么 ; 2.已知实数满足,,求的取值范围 3.已知1
板书设计 1.等式性质 2.不等式性质 例1 例2 例3. 练习
课后作业 完成作业。 完成课后作用,巩固回忆知识。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
