【核心素养目标】人教版(2019)高二化学选择性必修一1.2 反应热的计算
文档属性
| 名称 | 【核心素养目标】人教版(2019)高二化学选择性必修一1.2 反应热的计算 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-09-06 10:02:20 | ||
图片预览





文档简介
(共20张PPT)
第二节 反应热的计算
人教版选择性必修1
学习目标
1.通过盖斯定律的学习,理解盖斯定律,并能利用盖斯定律解决简单问题。
2.通过热化学方程式、中和热、燃烧热和盖斯定律的学习,能进行反应焓变的简单计算。
学习目标
1.通过从宏微的视角认识和掌握盖斯定律。培养学生“宏观辨识与微观探析”的学科素养。
2.通过认识化学变化的本质是有新物质生成,并伴有能量的转化,并遵循盖斯定律。培养学生“变化观念与平衡思想”的学科素养。
3.通过分析、推理等方法总结反应热与始态和终态的相互关系,建立认知模型,并能运用模型解决有关反应热的计算问题。培养学生“证据推理与模型认知”的学科素养。
素养目标
情境引入
在科学研究和工业生产中,常常需要了解反应热。许多反应热可以通过实验直接测定,但是有些反应热是无法直接测定的。例如,对于化学反应:
C 燃烧时不可能全部生成CO,总有一部分CO2生成,因此该反应的反应热是无法直接测定的。但这个反应热是冶金工业中非常有用的数据,应该如何获得呢?能否利用一些已知反应的反应热来计算其他反应的反应热呢?
教学过程
一、盖斯定律
一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。即在一定条件下,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
1.内容
2.本质
能量守恒定律
教学过程
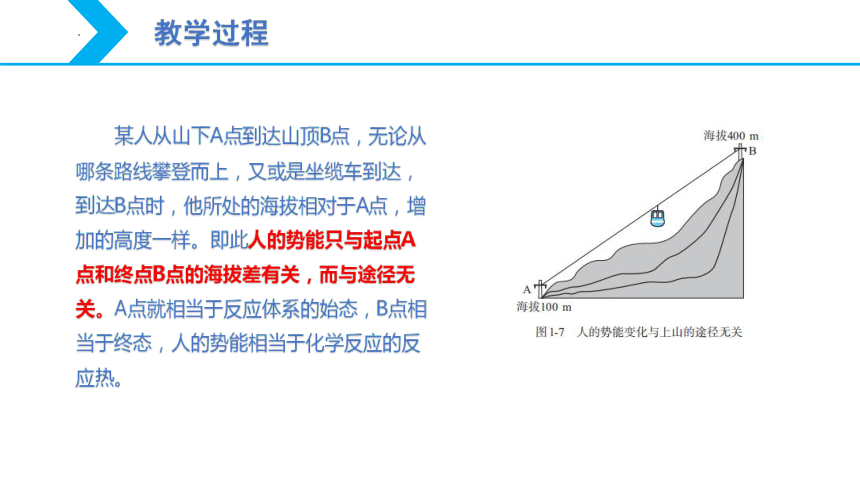
某人从山下A点到达山顶B点,无论从哪条路线攀登而上,又或是坐缆车到达,到达B点时,他所处的海拔相对于A点,增加的高度一样。即此人的势能只与起点A点和终点B点的海拔差有关,而与途径无关。A点就相当于反应体系的始态,B点相当于终态,人的势能相当于化学反应的反应热。
教学过程
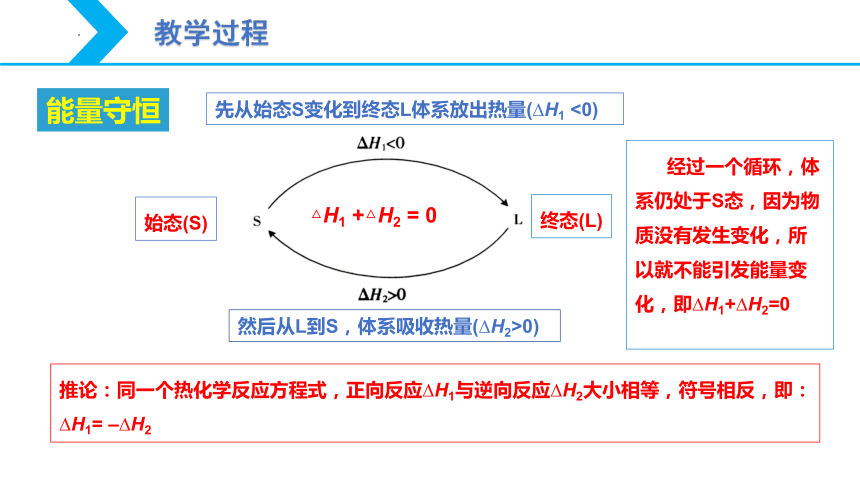
能量守恒
始态(S)
终态(L)
先从始态S变化到终态L体系放出热量( H1 <0)
然后从L到S,体系吸收热量( H2>0)
△H1 +△H2 = 0
经过一个循环,体系仍处于S态,因为物质没有发生变化,所以就不能引发能量变化,即 H1+ H2=0
推论:同一个热化学反应方程式,正向反应 H1与逆向反应 H2大小相等,符号相反,即: H1= – H2
教学过程
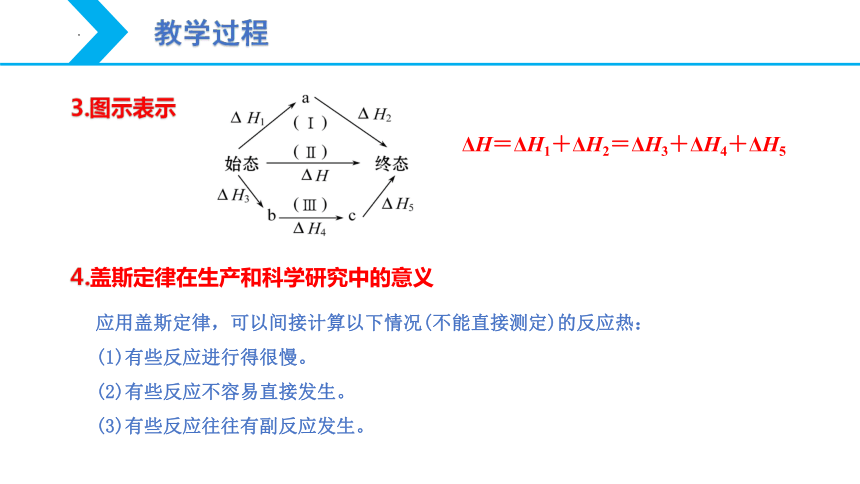
3.图示表示
ΔH=ΔH1+ΔH2=ΔH3+ΔH4+ΔH5
4.盖斯定律在生产和科学研究中的意义
应用盖斯定律,可以间接计算以下情况(不能直接测定)的反应热:
(1)有些反应进行得很慢。
(2)有些反应不容易直接发生。
(3)有些反应往往有副反应发生。
C(s)+ O2(g)
CO2(g)
△H1
△H3
△H1= △H2 + △H3
CO(g) + O2(g)
1
2
△H2
△H3 =△H1 - △H2
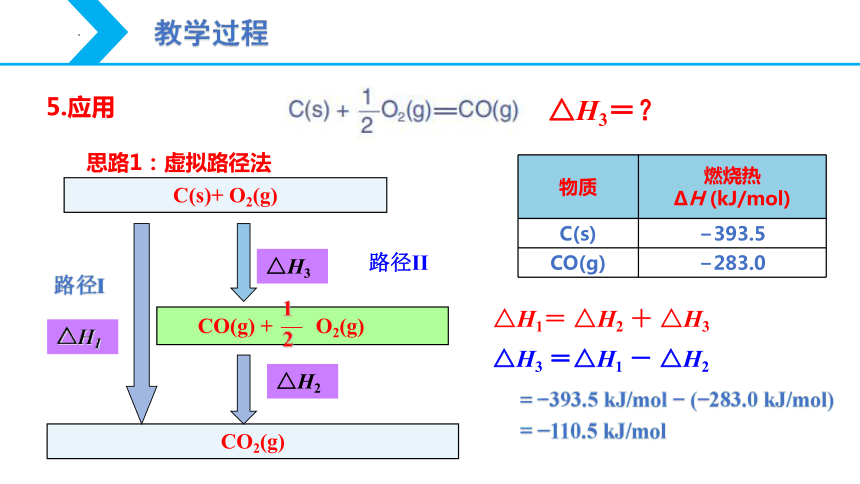
5.应用
△H3=?
物质 燃烧热
ΔH (kJ/mol)
C(s) 393.5
CO(g) 283.0
思路1:虚拟路径法
路径I
路径II
= 393.5 kJ/mol ( 283.0 kJ/mol)
= 110.5 kJ/mol
教学过程
加合法
即运用所给热化学方程式通过加减的方法得到所求热化学方程式。
思路2:代数运算法
教学过程
分析:找唯一:C、CO分别在Ⅰ、Ⅱ中出现一次
同侧加:C是Ⅰ中反应物,为同侧,则“+Ⅰ”
异侧减:CO是Ⅱ中反应物,为异侧,则“-Ⅱ”
调计量数:化学计量数相同,不用调整,则Ⅰ-Ⅱ即为运算式。
所以ΔH3=ΔH1-ΔH2=-110.5 kJ·mol-1。
Ⅰ.C(s)+O2(g)=CO2(g) ΔH1=-393.5 kJ·mol-1
-Ⅱ.CO(g)+ O2(g)=CO2(g) ΔH2=-283.0 kJ·mol-1
C(s)+ O2(g)=CO(g) ΔH3 =ΔH1-ΔH2=-110.5 kJ·mol-1
教学过程
思维模型
(1)确定待求反应的热化学方程式(目标反应方程式);
(2)找出待求热化学方程式中各物质出现在已知方程式中的位置(是同侧还是异侧);
(3)利用同侧相加、异侧相减进行处理;
(4)根据未知方程式中各物质的化学计量数通过乘除来调整已知反应的化学计量数,并消去中间产物;
(6)实施叠加并确定反应热的变化。
(7)把已知ΔH 带正负号进行与上述相同的四则运算规则进行计算即得目标方程式的ΔH 。
典例1.
课堂练习
已知下列反应的反应热
CH3COOH(l)+2O2(g)=2CO2(g)+2H2O(l) △H1= -870.3 kJ/mol
C(s) + O2 (g) = CO2(g) △H2= -393.5 kJ/mol
H2(g) + O2(g) =H2O(l) △H3=-285.8 kJ/mol
试计算下述反应的反应热:2C(s) + 2H2 (g) + O2 (g) = CH3COOH (l)
解: ④= ②×2 +③×2- ① △H4= 2△H2 +2△H3-△H1
2C(s) + 2O2 (g) = 2CO2(g) 2△H2= -787.0 kJ/mol
2H2(g) + O2(g) =2H2O(l) 2△H3= -571.6 kJ/mol
-) CH3COOH(l)+2O2(g)=2CO2(g)+2H2O(l) △H1= -870.3 kJ/mol
---------------------------------------------------------------------------------------------------
2C(s) +2H2(l)+O2(g)=CH3COOH(l) △H4= -488.3 kJ/mol
①
②
④
③
“嫦娥”五号预计在海南文昌发射中心发射,火箭的第一、二级发动机中,所用的燃料为偏二甲肼和四氧化二氮,偏二甲肼可用肼来制备。用肼(N2H4)作燃料,四氧化二氮作氧化剂,二者反应生成氮气和气态水。已知:
①N2(g)+2O2(g)=N2O4(g) ΔH=+10.7 kJ·mol-1
②N2H4(g)+O2(g)=N2(g)+2H2O(g) ΔH=-543 kJ·mol-1
写出气态肼和N2O4反应的热化学方程式: 。
课堂练习
典例2.
【答案】2N2H4(g)+N2O4(g)=3N2(g)+4H2O(g) ΔH=-1 096.7 kJ·mol-1
【解析】根据盖斯定律,由2×②-①得:2N2H4(g)+N2O4(g)=3N2(g)+4H2O(g) ΔH=2×(-543 kJ·mol-1) -(+10.7 kJ·mol-1)=-1 096.7 kJ·mol-1。
教学过程
教学过程
二、反应热计算
1.有关热化学方程式的计算
【例1】25 ℃、101 kPa时,使1.0 g钠与足量的氯气反应,生成氯化钠晶体并放出17.87 kJ的热量,求生成1 mol氯化钠的反应热。
解析: Na(s) + Cl2(g) = NaCl(s)
1 △H
1.0g÷ 23g/mol -17.87kJ
△H =-17.87×23=-411 kJ/mol
答:生成1 mol NaCl的反应热为△H =-411 kJ/mol。
教学过程
2.关于燃烧热的计算
【例2】乙醇的燃烧热ΔH=-1366.8 kJ/mol,在25℃、101 kPa时,1 kg乙醇充分燃烧后放出多少热量?
解析: n(C2H5OH)= =21.74 mol
1 -1366.8kJ
21.74 mol Q
1 kgC2H5OH燃烧后产生的热量:1366.8 kJ/mol× 21.74 mol=2.971×104 kJ
答:1 kg C2H5OH充分燃烧后放出2.971×104 kJ的热量。
C2H5OH (l) + 3O2(g)=2CO2(g)+3H2O (l)
反应热的计算方法
教学过程
教学过程
典例4.下图是通过热化学循环在较低温度下由水或硫化氢分解制备氢气的反应系统原理。
下图是通过热化学循环在较低温度下由水或硫化氢分解制备氢气的反应系统原理。
通过计算,可知系统(Ⅰ)和系统(Ⅱ)制氢的热化学方程式分别为
H2O(l)=H2(g)+2(1)O2(g) ΔH=286 kJ·mol-1、H2S(g)=H2(g)+S(s) ΔH=20 kJ·mol-1,
制得等量H2所需能量较少的是 。
典例4.
【解析】根据盖斯定律,将①+②+③可得,系统(Ⅰ)中的热化学方程式:H2O(l)=H2(g)+2(1)O2(g) ΔH=ΔH1+ΔH2+ΔH3=327 kJ·mol-1-151 kJ·mol-1+110 kJ·mol-1=286 kJ·mol-1同理,将②+③+④可得,系统(Ⅱ)中的热化学方程式:H2S(g)=H2(g)+S(s) ΔH=ΔH2+ΔH3+ΔH4=-151 kJ·mol-1+110 kJ·mol-1+61 kJ·mol-1=20 kJ·mol-1由所得两热化学方程式可知,制得等量H2所需能量较少的是系统(Ⅱ)。
教学过程
近年来,研究人员提出利用含硫物质热化学循环实现太阳能的转化与存储。过程如下:
反应Ⅰ:2H2SO4(l)===2SO2(g)+2H2O(g)+O2(g) ΔH1=+551 kJ·mol-1反应Ⅲ:S(s)+O2(g)===SO2(g) ΔH3=-297 kJ·mol-1
反应Ⅱ的热化学方程式: 。
典例5.
【答案】3SO2(g)+2H2O(g)=2H2SO4(l)+S(s) ΔH2=-254 kJ·mol-1
【解析】由题图可知,反应Ⅱ的化学方程式为3SO2+2H2O=2H2SO4+S↓。根据盖斯定律,反应Ⅱ=-(反应Ⅰ+反应Ⅲ)可得:3SO2(g)+2H2O(g)=2H2SO4(l)+S(s) ΔH2=-254 kJ·mol-1。
课堂小结
盖斯定律应用三步流程
感 谢 倾 听
第二节 反应热的计算
人教版选择性必修1
学习目标
1.通过盖斯定律的学习,理解盖斯定律,并能利用盖斯定律解决简单问题。
2.通过热化学方程式、中和热、燃烧热和盖斯定律的学习,能进行反应焓变的简单计算。
学习目标
1.通过从宏微的视角认识和掌握盖斯定律。培养学生“宏观辨识与微观探析”的学科素养。
2.通过认识化学变化的本质是有新物质生成,并伴有能量的转化,并遵循盖斯定律。培养学生“变化观念与平衡思想”的学科素养。
3.通过分析、推理等方法总结反应热与始态和终态的相互关系,建立认知模型,并能运用模型解决有关反应热的计算问题。培养学生“证据推理与模型认知”的学科素养。
素养目标
情境引入
在科学研究和工业生产中,常常需要了解反应热。许多反应热可以通过实验直接测定,但是有些反应热是无法直接测定的。例如,对于化学反应:
C 燃烧时不可能全部生成CO,总有一部分CO2生成,因此该反应的反应热是无法直接测定的。但这个反应热是冶金工业中非常有用的数据,应该如何获得呢?能否利用一些已知反应的反应热来计算其他反应的反应热呢?
教学过程
一、盖斯定律
一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。即在一定条件下,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
1.内容
2.本质
能量守恒定律
教学过程
某人从山下A点到达山顶B点,无论从哪条路线攀登而上,又或是坐缆车到达,到达B点时,他所处的海拔相对于A点,增加的高度一样。即此人的势能只与起点A点和终点B点的海拔差有关,而与途径无关。A点就相当于反应体系的始态,B点相当于终态,人的势能相当于化学反应的反应热。
教学过程
能量守恒
始态(S)
终态(L)
先从始态S变化到终态L体系放出热量( H1 <0)
然后从L到S,体系吸收热量( H2>0)
△H1 +△H2 = 0
经过一个循环,体系仍处于S态,因为物质没有发生变化,所以就不能引发能量变化,即 H1+ H2=0
推论:同一个热化学反应方程式,正向反应 H1与逆向反应 H2大小相等,符号相反,即: H1= – H2
教学过程
3.图示表示
ΔH=ΔH1+ΔH2=ΔH3+ΔH4+ΔH5
4.盖斯定律在生产和科学研究中的意义
应用盖斯定律,可以间接计算以下情况(不能直接测定)的反应热:
(1)有些反应进行得很慢。
(2)有些反应不容易直接发生。
(3)有些反应往往有副反应发生。
C(s)+ O2(g)
CO2(g)
△H1
△H3
△H1= △H2 + △H3
CO(g) + O2(g)
1
2
△H2
△H3 =△H1 - △H2
5.应用
△H3=?
物质 燃烧热
ΔH (kJ/mol)
C(s) 393.5
CO(g) 283.0
思路1:虚拟路径法
路径I
路径II
= 393.5 kJ/mol ( 283.0 kJ/mol)
= 110.5 kJ/mol
教学过程
加合法
即运用所给热化学方程式通过加减的方法得到所求热化学方程式。
思路2:代数运算法
教学过程
分析:找唯一:C、CO分别在Ⅰ、Ⅱ中出现一次
同侧加:C是Ⅰ中反应物,为同侧,则“+Ⅰ”
异侧减:CO是Ⅱ中反应物,为异侧,则“-Ⅱ”
调计量数:化学计量数相同,不用调整,则Ⅰ-Ⅱ即为运算式。
所以ΔH3=ΔH1-ΔH2=-110.5 kJ·mol-1。
Ⅰ.C(s)+O2(g)=CO2(g) ΔH1=-393.5 kJ·mol-1
-Ⅱ.CO(g)+ O2(g)=CO2(g) ΔH2=-283.0 kJ·mol-1
C(s)+ O2(g)=CO(g) ΔH3 =ΔH1-ΔH2=-110.5 kJ·mol-1
教学过程
思维模型
(1)确定待求反应的热化学方程式(目标反应方程式);
(2)找出待求热化学方程式中各物质出现在已知方程式中的位置(是同侧还是异侧);
(3)利用同侧相加、异侧相减进行处理;
(4)根据未知方程式中各物质的化学计量数通过乘除来调整已知反应的化学计量数,并消去中间产物;
(6)实施叠加并确定反应热的变化。
(7)把已知ΔH 带正负号进行与上述相同的四则运算规则进行计算即得目标方程式的ΔH 。
典例1.
课堂练习
已知下列反应的反应热
CH3COOH(l)+2O2(g)=2CO2(g)+2H2O(l) △H1= -870.3 kJ/mol
C(s) + O2 (g) = CO2(g) △H2= -393.5 kJ/mol
H2(g) + O2(g) =H2O(l) △H3=-285.8 kJ/mol
试计算下述反应的反应热:2C(s) + 2H2 (g) + O2 (g) = CH3COOH (l)
解: ④= ②×2 +③×2- ① △H4= 2△H2 +2△H3-△H1
2C(s) + 2O2 (g) = 2CO2(g) 2△H2= -787.0 kJ/mol
2H2(g) + O2(g) =2H2O(l) 2△H3= -571.6 kJ/mol
-) CH3COOH(l)+2O2(g)=2CO2(g)+2H2O(l) △H1= -870.3 kJ/mol
---------------------------------------------------------------------------------------------------
2C(s) +2H2(l)+O2(g)=CH3COOH(l) △H4= -488.3 kJ/mol
①
②
④
③
“嫦娥”五号预计在海南文昌发射中心发射,火箭的第一、二级发动机中,所用的燃料为偏二甲肼和四氧化二氮,偏二甲肼可用肼来制备。用肼(N2H4)作燃料,四氧化二氮作氧化剂,二者反应生成氮气和气态水。已知:
①N2(g)+2O2(g)=N2O4(g) ΔH=+10.7 kJ·mol-1
②N2H4(g)+O2(g)=N2(g)+2H2O(g) ΔH=-543 kJ·mol-1
写出气态肼和N2O4反应的热化学方程式: 。
课堂练习
典例2.
【答案】2N2H4(g)+N2O4(g)=3N2(g)+4H2O(g) ΔH=-1 096.7 kJ·mol-1
【解析】根据盖斯定律,由2×②-①得:2N2H4(g)+N2O4(g)=3N2(g)+4H2O(g) ΔH=2×(-543 kJ·mol-1) -(+10.7 kJ·mol-1)=-1 096.7 kJ·mol-1。
教学过程
教学过程
二、反应热计算
1.有关热化学方程式的计算
【例1】25 ℃、101 kPa时,使1.0 g钠与足量的氯气反应,生成氯化钠晶体并放出17.87 kJ的热量,求生成1 mol氯化钠的反应热。
解析: Na(s) + Cl2(g) = NaCl(s)
1 △H
1.0g÷ 23g/mol -17.87kJ
△H =-17.87×23=-411 kJ/mol
答:生成1 mol NaCl的反应热为△H =-411 kJ/mol。
教学过程
2.关于燃烧热的计算
【例2】乙醇的燃烧热ΔH=-1366.8 kJ/mol,在25℃、101 kPa时,1 kg乙醇充分燃烧后放出多少热量?
解析: n(C2H5OH)= =21.74 mol
1 -1366.8kJ
21.74 mol Q
1 kgC2H5OH燃烧后产生的热量:1366.8 kJ/mol× 21.74 mol=2.971×104 kJ
答:1 kg C2H5OH充分燃烧后放出2.971×104 kJ的热量。
C2H5OH (l) + 3O2(g)=2CO2(g)+3H2O (l)
反应热的计算方法
教学过程
教学过程
典例4.下图是通过热化学循环在较低温度下由水或硫化氢分解制备氢气的反应系统原理。
下图是通过热化学循环在较低温度下由水或硫化氢分解制备氢气的反应系统原理。
通过计算,可知系统(Ⅰ)和系统(Ⅱ)制氢的热化学方程式分别为
H2O(l)=H2(g)+2(1)O2(g) ΔH=286 kJ·mol-1、H2S(g)=H2(g)+S(s) ΔH=20 kJ·mol-1,
制得等量H2所需能量较少的是 。
典例4.
【解析】根据盖斯定律,将①+②+③可得,系统(Ⅰ)中的热化学方程式:H2O(l)=H2(g)+2(1)O2(g) ΔH=ΔH1+ΔH2+ΔH3=327 kJ·mol-1-151 kJ·mol-1+110 kJ·mol-1=286 kJ·mol-1同理,将②+③+④可得,系统(Ⅱ)中的热化学方程式:H2S(g)=H2(g)+S(s) ΔH=ΔH2+ΔH3+ΔH4=-151 kJ·mol-1+110 kJ·mol-1+61 kJ·mol-1=20 kJ·mol-1由所得两热化学方程式可知,制得等量H2所需能量较少的是系统(Ⅱ)。
教学过程
近年来,研究人员提出利用含硫物质热化学循环实现太阳能的转化与存储。过程如下:
反应Ⅰ:2H2SO4(l)===2SO2(g)+2H2O(g)+O2(g) ΔH1=+551 kJ·mol-1反应Ⅲ:S(s)+O2(g)===SO2(g) ΔH3=-297 kJ·mol-1
反应Ⅱ的热化学方程式: 。
典例5.
【答案】3SO2(g)+2H2O(g)=2H2SO4(l)+S(s) ΔH2=-254 kJ·mol-1
【解析】由题图可知,反应Ⅱ的化学方程式为3SO2+2H2O=2H2SO4+S↓。根据盖斯定律,反应Ⅱ=-(反应Ⅰ+反应Ⅲ)可得:3SO2(g)+2H2O(g)=2H2SO4(l)+S(s) ΔH2=-254 kJ·mol-1。
课堂小结
盖斯定律应用三步流程
感 谢 倾 听
