30.2二次函数的图像和性质基础练习-冀教版数学九年级下册(含答案)
文档属性
| 名称 | 30.2二次函数的图像和性质基础练习-冀教版数学九年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 256.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 21:02:57 | ||
图片预览


文档简介
30.2二次函数的图像和性质基础练习-冀教版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将抛物线y=x2-4x-3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A.y=(x+1)2-2 B.y=(x-5)2-2 C.y=(x-5)2-12 D.y=(x+1)2-12
2.由二次函数可知( )
A.其图象的开口向上 B.其顶点坐标为
C.其图象的对称轴为直线 D.当时,y随x的增大而增大
3.关于二次函数,下列说法正确的是( )
A.函数图象的开口向下 B.当时,y随x的增大而增大
C.该函数有最大值,是大值是5 D.函数图象的顶点坐标是
4.抛物线y=x2﹣4x+4的顶点坐标为( )
A.(﹣4,4) B.(﹣2,0) C.(2,0) D.(﹣4,0)
5.已知点在二次函数的图象上,当时,则m的取值范围是( )
A. B. C. D.
6.将抛物线先向右平移4个单位,再向上平移3个单位后,所得的抛物线解析式为,则原抛物线的解析式是( )
A. B.
C. D.
7.已知抛物线 过A ,B ,C 三点,则 大小关系是( )
A. B. C. D.
8.将二次函数y=x2的图象先向左平移2个单位,再向上平移3个单位,得到的二次函数的表达式为( )
A.y=2x2+3 B.y=﹣2x2﹣3 C.y=(x﹣2)2﹣3 D.y=(x+2)2+3
9.已知点是二次函数的图像上的一个点.点也在该函数图像上的一点,若m是关于x的方程的根,则( )
A. B. C. D.
10.若点,,在抛物线上,则下列结论正确的是( )
A. B. C. D.
二、填空题
11.抛物线的最小值是 .
12.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点,若二次函数(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是 .
13.二次函数的图象的对称轴是经过点的一条直线,则 .
14.我们规定:若,则.例如,则.已知,且,则的最大值是 .
15.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,抛物线与x轴的另一个交点坐标为 .
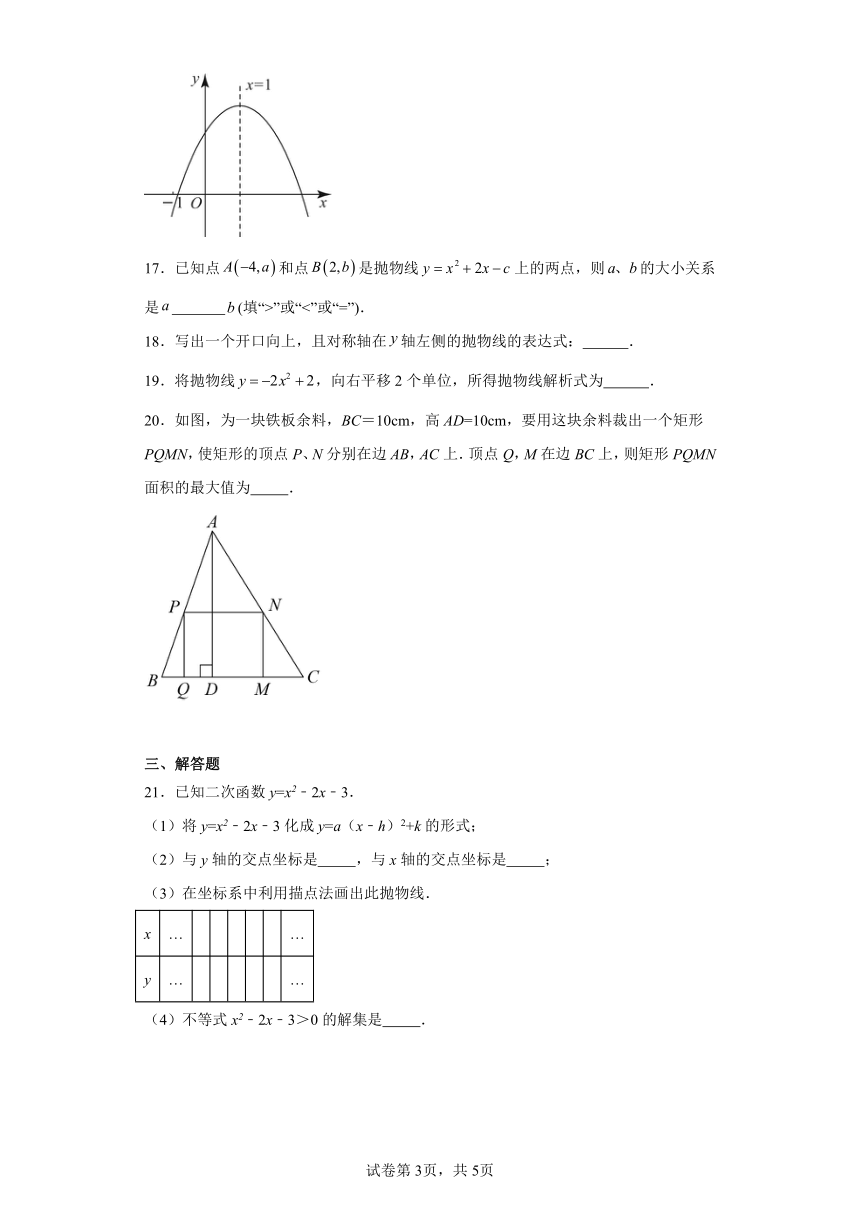
16.已知函数 的部分图象如下图所示,当x 时,y随x的增大而减小.
17.已知点和点是抛物线上的两点,则的大小关系是 (填“>”或“<”或“=”).
18.写出一个开口向上,且对称轴在轴左侧的抛物线的表达式: .
19.将抛物线,向右平移2个单位,所得抛物线解析式为 .
20.如图,为一块铁板余料,BC=10cm,高AD=10cm,要用这块余料裁出一个矩形PQMN,使矩形的顶点P、N分别在边AB,AC上.顶点Q,M在边BC上,则矩形PQMN面积的最大值为 .
三、解答题
21.已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 ,与x轴的交点坐标是 ;
(3)在坐标系中利用描点法画出此抛物线.
x … …
y … …
(4)不等式x2﹣2x﹣3>0的解集是 .
22.已知抛物线G:y=x2+(k﹣5)x+1﹣k,其中k为常数.
(1)求证:无论k为何值,抛物线G总与x轴有两个交点;
(2)若抛物线G的图象不经过第三象限,求k的取值范围;
(3)对于一个函数,当自变量x取a时,函数值y也等于a,我们称a为这个函数的对等值.若函数y=x2+(k﹣5)x+1﹣k有两相异的对等值x1,x2,且x1<2<x2,求k的最大整数值.
23.已知二次函数.
(1)在平面直角坐标系中画出函数的图象;
(2)若时,则y的取值范围是______.
24.已知抛物线y=x2+bx+c与x轴交于点A(-3,0)、B(1,0),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求b、c的值;
(2)求∠DAO的度数和线段AD的长;
(3)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′,若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
25.如图,抛物线的顶点为A,对称轴与x轴交于点C,当以为对角线的正方形的另外两个顶点B、D恰好在抛物线上时,我们把这样的抛物线称为“美丽抛物线”,正方形为它的内接正方形.
(1)当抛物线是“美丽抛物线”时,则 ;
(2)当抛物线是“美丽抛物线”时,则 ;
(3)若抛物线是“美丽抛物线”,求a,k之间的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.B
4.C
5.B
6.B
7.A
8.D
9.C
10.B
11.-11
12.
13.-1
14.8
15.
16./大于1
17.=
18.(答案不唯一)
19.
20.25
21.();(),,;()见解析;()或.
22.(1)略;(2)k≤1;(3)k的最大整数值为6
23.(1)略
(2)
24.(1)b=2,c=-3(2)∠DAO=45°.AD=3(3)y=x2-4x+3或y=x2+6x+3
25.(1)
(2)4
(3)
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将抛物线y=x2-4x-3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A.y=(x+1)2-2 B.y=(x-5)2-2 C.y=(x-5)2-12 D.y=(x+1)2-12
2.由二次函数可知( )
A.其图象的开口向上 B.其顶点坐标为
C.其图象的对称轴为直线 D.当时,y随x的增大而增大
3.关于二次函数,下列说法正确的是( )
A.函数图象的开口向下 B.当时,y随x的增大而增大
C.该函数有最大值,是大值是5 D.函数图象的顶点坐标是
4.抛物线y=x2﹣4x+4的顶点坐标为( )
A.(﹣4,4) B.(﹣2,0) C.(2,0) D.(﹣4,0)
5.已知点在二次函数的图象上,当时,则m的取值范围是( )
A. B. C. D.
6.将抛物线先向右平移4个单位,再向上平移3个单位后,所得的抛物线解析式为,则原抛物线的解析式是( )
A. B.
C. D.
7.已知抛物线 过A ,B ,C 三点,则 大小关系是( )
A. B. C. D.
8.将二次函数y=x2的图象先向左平移2个单位,再向上平移3个单位,得到的二次函数的表达式为( )
A.y=2x2+3 B.y=﹣2x2﹣3 C.y=(x﹣2)2﹣3 D.y=(x+2)2+3
9.已知点是二次函数的图像上的一个点.点也在该函数图像上的一点,若m是关于x的方程的根,则( )
A. B. C. D.
10.若点,,在抛物线上,则下列结论正确的是( )
A. B. C. D.
二、填空题
11.抛物线的最小值是 .
12.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点,若二次函数(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是 .
13.二次函数的图象的对称轴是经过点的一条直线,则 .
14.我们规定:若,则.例如,则.已知,且,则的最大值是 .
15.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,抛物线与x轴的另一个交点坐标为 .
16.已知函数 的部分图象如下图所示,当x 时,y随x的增大而减小.
17.已知点和点是抛物线上的两点,则的大小关系是 (填“>”或“<”或“=”).
18.写出一个开口向上,且对称轴在轴左侧的抛物线的表达式: .
19.将抛物线,向右平移2个单位,所得抛物线解析式为 .
20.如图,为一块铁板余料,BC=10cm,高AD=10cm,要用这块余料裁出一个矩形PQMN,使矩形的顶点P、N分别在边AB,AC上.顶点Q,M在边BC上,则矩形PQMN面积的最大值为 .
三、解答题
21.已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 ,与x轴的交点坐标是 ;
(3)在坐标系中利用描点法画出此抛物线.
x … …
y … …
(4)不等式x2﹣2x﹣3>0的解集是 .
22.已知抛物线G:y=x2+(k﹣5)x+1﹣k,其中k为常数.
(1)求证:无论k为何值,抛物线G总与x轴有两个交点;
(2)若抛物线G的图象不经过第三象限,求k的取值范围;
(3)对于一个函数,当自变量x取a时,函数值y也等于a,我们称a为这个函数的对等值.若函数y=x2+(k﹣5)x+1﹣k有两相异的对等值x1,x2,且x1<2<x2,求k的最大整数值.
23.已知二次函数.
(1)在平面直角坐标系中画出函数的图象;
(2)若时,则y的取值范围是______.
24.已知抛物线y=x2+bx+c与x轴交于点A(-3,0)、B(1,0),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求b、c的值;
(2)求∠DAO的度数和线段AD的长;
(3)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′,若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
25.如图,抛物线的顶点为A,对称轴与x轴交于点C,当以为对角线的正方形的另外两个顶点B、D恰好在抛物线上时,我们把这样的抛物线称为“美丽抛物线”,正方形为它的内接正方形.
(1)当抛物线是“美丽抛物线”时,则 ;
(2)当抛物线是“美丽抛物线”时,则 ;
(3)若抛物线是“美丽抛物线”,求a,k之间的数量关系.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.B
4.C
5.B
6.B
7.A
8.D
9.C
10.B
11.-11
12.
13.-1
14.8
15.
16./大于1
17.=
18.(答案不唯一)
19.
20.25
21.();(),,;()见解析;()或.
22.(1)略;(2)k≤1;(3)k的最大整数值为6
23.(1)略
(2)
24.(1)b=2,c=-3(2)∠DAO=45°.AD=3(3)y=x2-4x+3或y=x2+6x+3
25.(1)
(2)4
(3)
答案第1页,共2页
答案第1页,共2页
