2022—2023学年人教版七年级数学上册1.2.3 相反数 导学案 (表格式 无答案)
文档属性
| 名称 | 2022—2023学年人教版七年级数学上册1.2.3 相反数 导学案 (表格式 无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 00:00:00 | ||
图片预览


文档简介
七年级数学上册导学案
课题 1.2.3 相反数
课型 讲授课 主备 审核
学习 目标 1.了解相反数的概念。 2.能在数轴上表示出两个互为相反数的数,并且发现表示互为相反数的两点在原点的两侧,到原点的距离相等。 3.利用互为相反数符号表示方法化简多重符号。 4.渗透数形结合等思想方法,并注意培养学生的概括能力。
学习 重点 相反数的概念及其表示方法,理解相反数的代数定义和几何定义的一致性。
学习 难点 负数的相反数的表示方法。
预 习 案 活动:要求两个学生背靠背站在同一位置,然后一个向右走5步,一个向左走5步 问题1:如果向右为正,向右走5步,向左走5步各记作什么? 问题2:在数轴上,画出表示+5,-5的点,并观察表示它们的点具有怎样的特征? 问题3:举出几组具有这样特征的两个数。
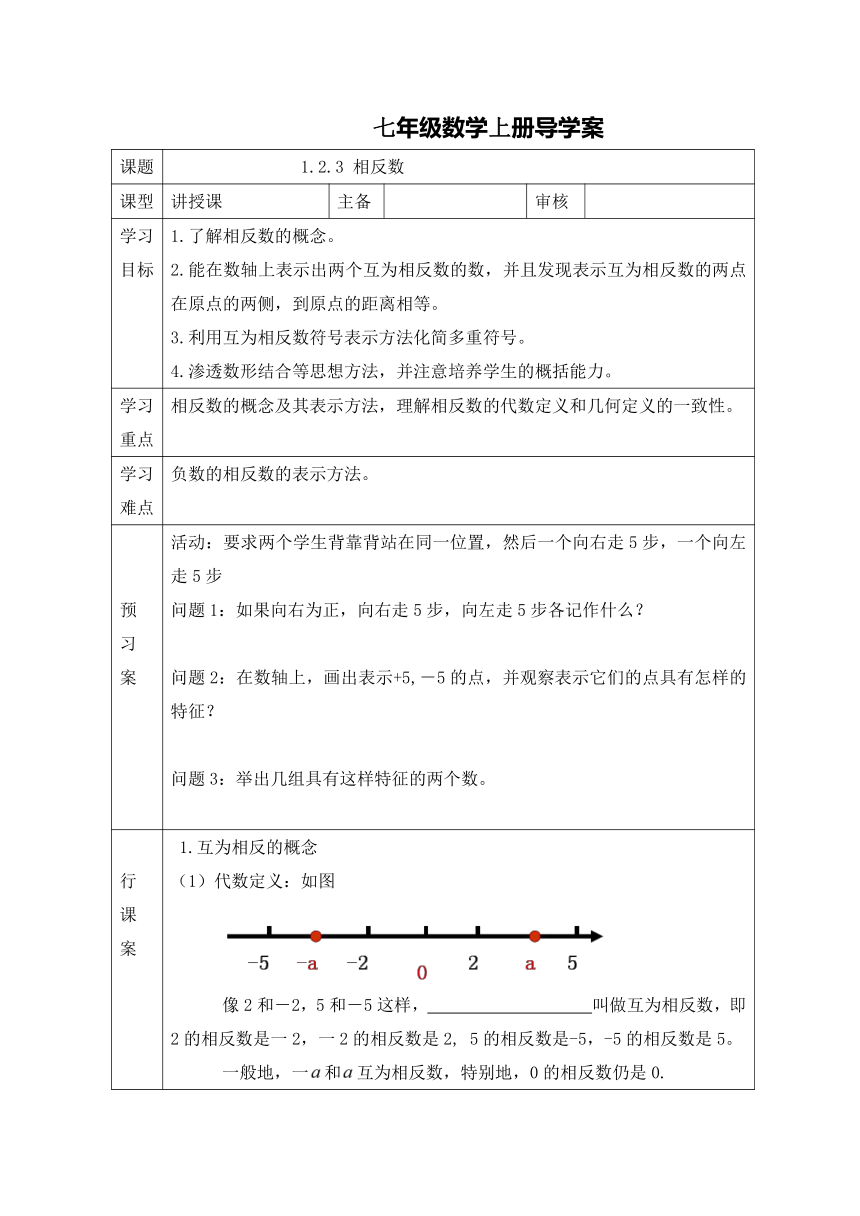
行 课 案 1.互为相反的概念 (1)代数定义:如图 像2和-2,5和-5这样, 叫做互为相反数,即2的相反数是一2,一2的相反数是2, 5的相反数是-5,-5的相反数是5。 一般地,一和互为相反数,特别地,0的相反数仍是0. (2)几何定义:在数轴上原点的两旁,离开原点距离 的两个点所表示的数,叫做互为相反数。如图,2与一2互为相反数,5与-5互为相反数。 2.一般地,设是一个正数,数轴上与原点的距离是的点有 ,它们分别在原点的左右两边,表示一和这两个数,我们说表示一和这两个数的点关于原点 。 3:如何深刻地认识互为相反数呢? 知识巩固: 例1分别写出下列各数的相反数 归纳:互为相反数的表示方法: 例2化简 -(-2.5),-(+3),+(-0.7) 跟踪练习: 1.求下列各数的相反数: (1)-5 (2) (3)0 (4) (5)-2b (6)a-b (7)a+2 2.判断: (1)-2是-(-2)的相反数; (2)-3和+3都是相反数; (3)-3是3的相反数; (4)-3与+3互为相反数; (5)+3是-3的相反数; (6)一个数的相反数不可能是它本身; (7) 符号相反的两个数叫做互为相反数; (8)互为相反数的两个数不一定一个是正数,一个是负数; (9)相反数和我们以前学过的倒数是一样的. 3.化简下列各数: (1)+(-10.1); (2)-(-16); (3)+(-12); (4)+(-0).
检 测 案 1. 2022的相反数是( ) A.2022 B.﹣2022 C. D. 2.如果实数a与3互为相反数,那么a是( ) A. B. C.3 D.﹣3 3.﹣a的相反数是 ,﹣b的相反数是﹣5,则b= . 4.下列两个数互为相反数的是( ) A.()和﹣() B.﹣0.5和 C.π和﹣3.14 D.+20和﹣(﹣20) 5.化简下列各数:﹣(+1)= ;﹣(﹣5)= ,﹣[+(﹣1)]= . 6.下列各对数中,互为相反数的是( ) A.﹣(+1)和+(﹣1) B.﹣(﹣1)和+(﹣1) C.﹣(+1)和﹣1 D.+(﹣1)和﹣1 +3与 互为相反数,只有 的相反数是它本身. 8.(拓展题)如图所示,已知A,B,C,D四个点在一条没有标明原点的数轴上. (1)若点A和点C表示的数互为相反数,则原点为 ; (2)若点B和点D表示的数互为相反数,则原点为 ; (3)若点A和点D表示的数互为相反数,则在数轴上表示出原点O的位置.
课题 1.2.3 相反数
课型 讲授课 主备 审核
学习 目标 1.了解相反数的概念。 2.能在数轴上表示出两个互为相反数的数,并且发现表示互为相反数的两点在原点的两侧,到原点的距离相等。 3.利用互为相反数符号表示方法化简多重符号。 4.渗透数形结合等思想方法,并注意培养学生的概括能力。
学习 重点 相反数的概念及其表示方法,理解相反数的代数定义和几何定义的一致性。
学习 难点 负数的相反数的表示方法。
预 习 案 活动:要求两个学生背靠背站在同一位置,然后一个向右走5步,一个向左走5步 问题1:如果向右为正,向右走5步,向左走5步各记作什么? 问题2:在数轴上,画出表示+5,-5的点,并观察表示它们的点具有怎样的特征? 问题3:举出几组具有这样特征的两个数。
行 课 案 1.互为相反的概念 (1)代数定义:如图 像2和-2,5和-5这样, 叫做互为相反数,即2的相反数是一2,一2的相反数是2, 5的相反数是-5,-5的相反数是5。 一般地,一和互为相反数,特别地,0的相反数仍是0. (2)几何定义:在数轴上原点的两旁,离开原点距离 的两个点所表示的数,叫做互为相反数。如图,2与一2互为相反数,5与-5互为相反数。 2.一般地,设是一个正数,数轴上与原点的距离是的点有 ,它们分别在原点的左右两边,表示一和这两个数,我们说表示一和这两个数的点关于原点 。 3:如何深刻地认识互为相反数呢? 知识巩固: 例1分别写出下列各数的相反数 归纳:互为相反数的表示方法: 例2化简 -(-2.5),-(+3),+(-0.7) 跟踪练习: 1.求下列各数的相反数: (1)-5 (2) (3)0 (4) (5)-2b (6)a-b (7)a+2 2.判断: (1)-2是-(-2)的相反数; (2)-3和+3都是相反数; (3)-3是3的相反数; (4)-3与+3互为相反数; (5)+3是-3的相反数; (6)一个数的相反数不可能是它本身; (7) 符号相反的两个数叫做互为相反数; (8)互为相反数的两个数不一定一个是正数,一个是负数; (9)相反数和我们以前学过的倒数是一样的. 3.化简下列各数: (1)+(-10.1); (2)-(-16); (3)+(-12); (4)+(-0).
检 测 案 1. 2022的相反数是( ) A.2022 B.﹣2022 C. D. 2.如果实数a与3互为相反数,那么a是( ) A. B. C.3 D.﹣3 3.﹣a的相反数是 ,﹣b的相反数是﹣5,则b= . 4.下列两个数互为相反数的是( ) A.()和﹣() B.﹣0.5和 C.π和﹣3.14 D.+20和﹣(﹣20) 5.化简下列各数:﹣(+1)= ;﹣(﹣5)= ,﹣[+(﹣1)]= . 6.下列各对数中,互为相反数的是( ) A.﹣(+1)和+(﹣1) B.﹣(﹣1)和+(﹣1) C.﹣(+1)和﹣1 D.+(﹣1)和﹣1 +3与 互为相反数,只有 的相反数是它本身. 8.(拓展题)如图所示,已知A,B,C,D四个点在一条没有标明原点的数轴上. (1)若点A和点C表示的数互为相反数,则原点为 ; (2)若点B和点D表示的数互为相反数,则原点为 ; (3)若点A和点D表示的数互为相反数,则在数轴上表示出原点O的位置.
