2023--2024学年北师大版八年级数学上册第1章 《勾股定理》单元过关检测卷(无答案)
文档属性
| 名称 | 2023--2024学年北师大版八年级数学上册第1章 《勾股定理》单元过关检测卷(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 00:00:00 | ||
图片预览

文档简介
北师大版八年级上册数学《勾股定理》单元过关检测卷
时间:90分钟 总分:120分
选择题(40分)
题号 1 2 3 4 5 6 7 8 9 10
选项
1. 直角三角形中有两边的长为3和4,那么第三边的长有( )
A.1个 B.2个 C.3个 D.4个
2. 下列四组线段中,可以构成直角三角形的是( )
A.4cm、5cm、6cm B.1cm、1.5cm、3cm
C.2cm、3cm、4cm D.1.5cm、2cm、2.5cm
3. 如图,点,都在格点上,若,则的长为( )
A. B. C. D.
4.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )
A.3cm B.4cm C.5cm D.6cm
5. 如图,在3×4的正方形网格(每个小正方形的边长都是1)中,标记格点A,B,C,D,则下列线段长度为的是( )
A.线段AB B.线段BC C.线段AC D.线段BD
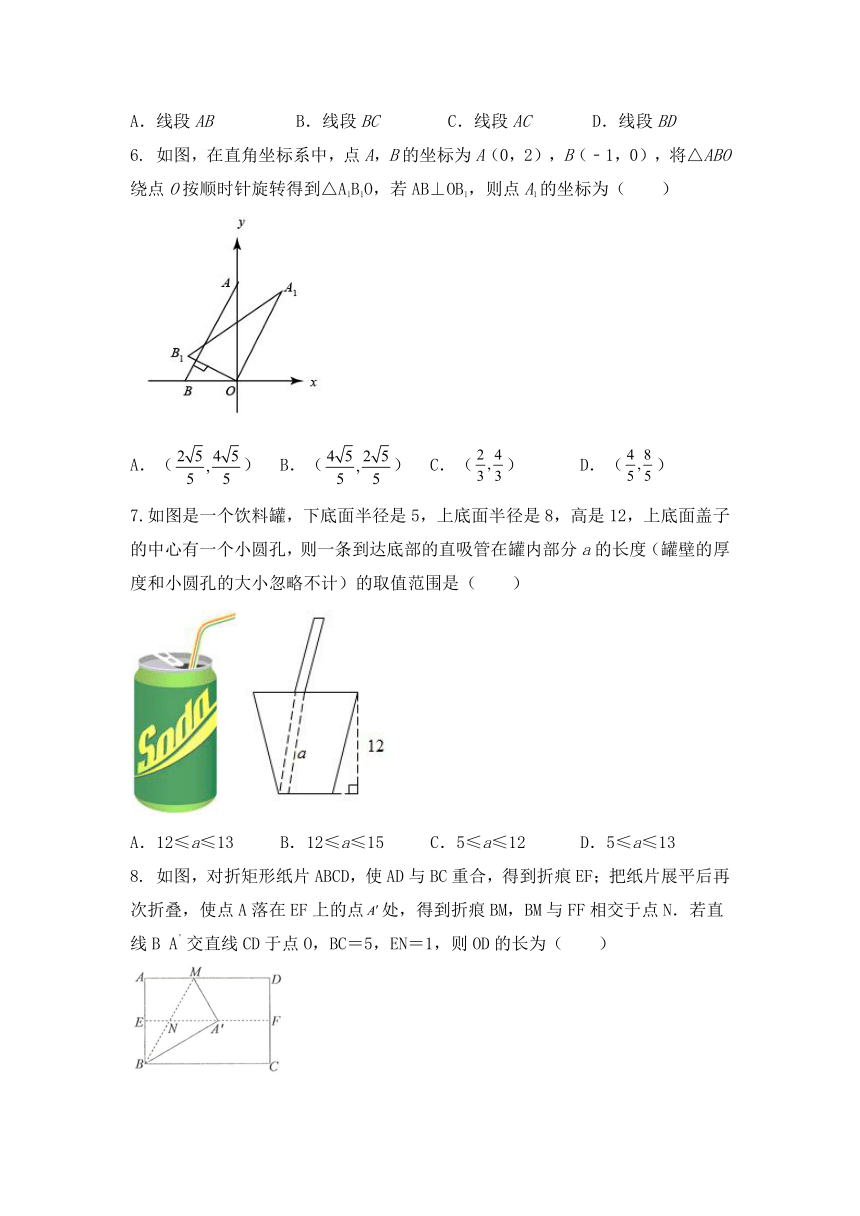
6. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1,则点A1的坐标为( )
A.() B.() C.() D.()
7.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
8. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
B. C. D.
9.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
A.76 B.72 C.68 D.52
10. 如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
A. B. C. D.
二、填空题(32分)
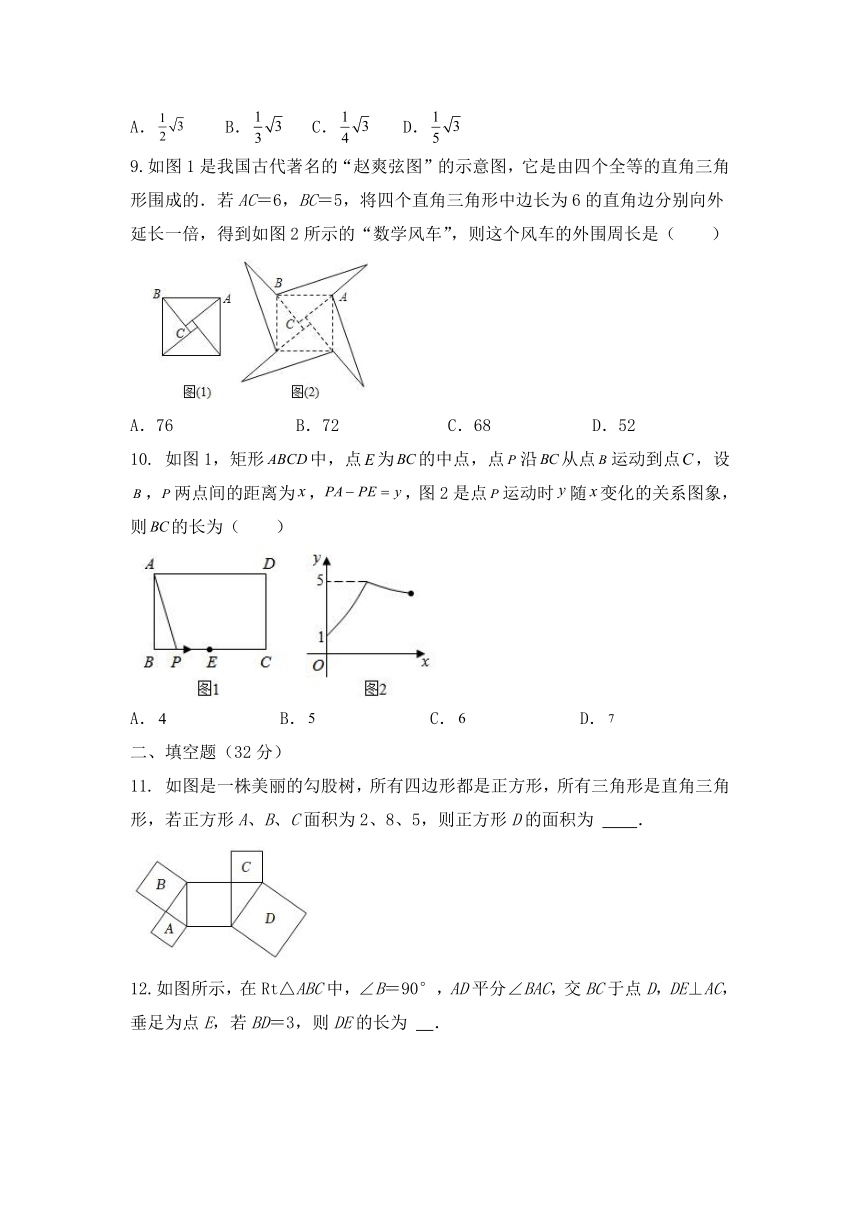
11. 如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为 .
12.如图所示,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为 .
13.如图,作一个以数轴的原点为圆心,长方形对角线为半径的圆弧,交数轴于点A,则点A表示的数是 .
14.如图,一架梯子AB长10米,底端离墙的距离BC为6米,当梯子下滑到DE时,AD=2米,则BE= 米.
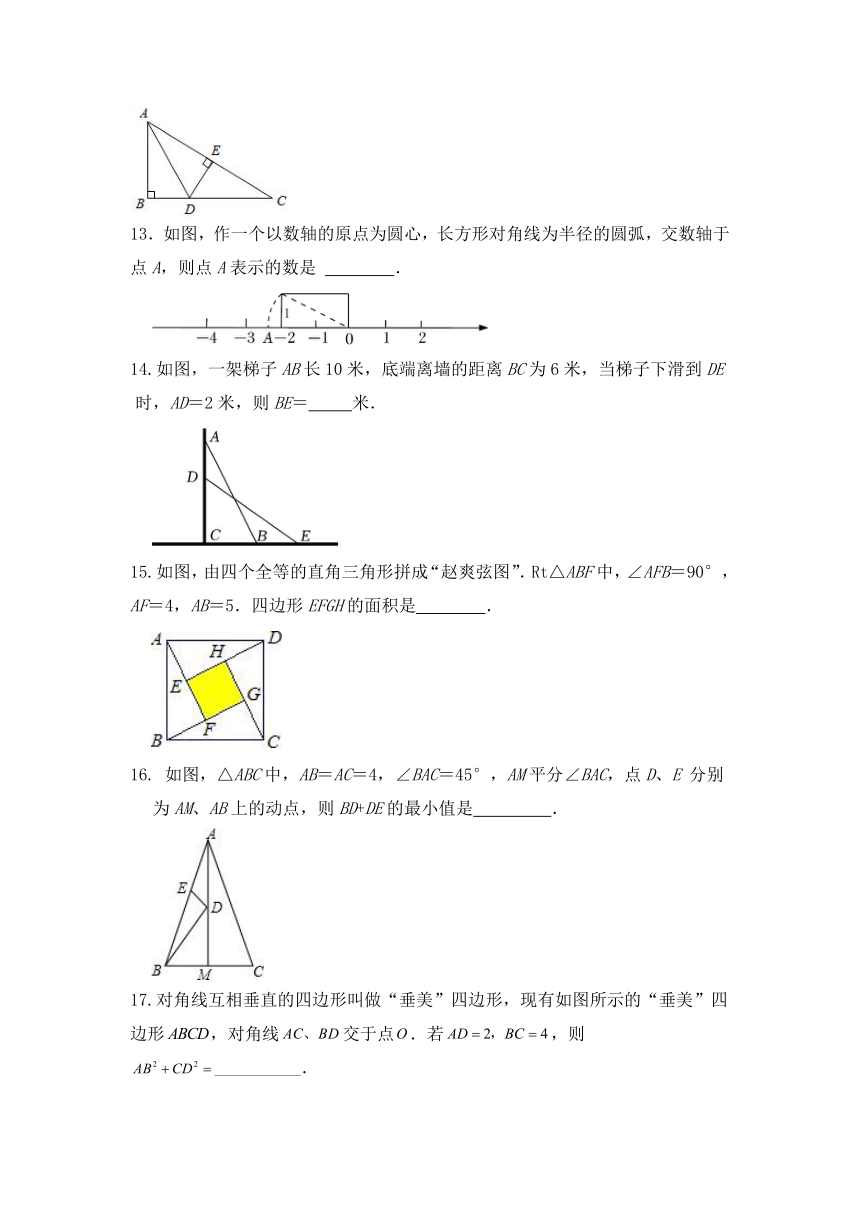
15.如图,由四个全等的直角三角形拼成“赵爽弦图”.Rt△ABF中,∠AFB=90°,AF=4,AB=5.四边形EFGH的面积是 .
16. 如图,△ABC中,AB=AC=4,∠BAC=45°,AM平分∠BAC,点D、E 分别为AM、AB上的动点,则BD+DE的最小值是 .
17.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线交于点.若,则__________.
18. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=10,D是BC的中点,E是AC上一动点,将△CDE沿DE折叠到△C'DE,连接AC',当△AEC'是直角三角形时,CE的长为 .
三、解答题(48分)。
19. .如图所示,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.
20. 如图,在△ABC中,∠ACB=90°,,.
(1)求AB的长度;
(2)已知D是AB上一点,连接CD,当CD的长度最短时,求AD的长度.
21. 如图,在Rt△ABC中,∠C=90°,AC=8,在△ABE中,DE是AB边上的高,DE=8,S△ABE=40.求BC的长度.
22. 如图,一辆小汽车在一条限速40km/h的街路上沿直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方60m处的C点,过了8s后,测得小汽车所在的B点与车速检测仪A之间的距离为100m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.
23. 在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
24.【图形定义】
我们把对角线互相垂直的四边形叫做垂美四边形.
【性质探究】
如图1,四边形ABCD是垂美四边形,试探究两组对边AB,CD与BC,AD之间的数量关系,并证明你的结论;
【拓展应用】
如图2,Rt△ACB中,∠ACB=90°,分别以AC和AB为直角边向外作等腰Rt△ACD和等腰Rt△ABE,连接DE,若AC=4,AB=5,求DE的长.
时间:90分钟 总分:120分
选择题(40分)
题号 1 2 3 4 5 6 7 8 9 10
选项
1. 直角三角形中有两边的长为3和4,那么第三边的长有( )
A.1个 B.2个 C.3个 D.4个
2. 下列四组线段中,可以构成直角三角形的是( )
A.4cm、5cm、6cm B.1cm、1.5cm、3cm
C.2cm、3cm、4cm D.1.5cm、2cm、2.5cm
3. 如图,点,都在格点上,若,则的长为( )
A. B. C. D.
4.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是( )
A.3cm B.4cm C.5cm D.6cm
5. 如图,在3×4的正方形网格(每个小正方形的边长都是1)中,标记格点A,B,C,D,则下列线段长度为的是( )
A.线段AB B.线段BC C.线段AC D.线段BD
6. 如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1,则点A1的坐标为( )
A.() B.() C.() D.()
7.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
8. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
B. C. D.
9.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
A.76 B.72 C.68 D.52
10. 如图1,矩形中,点为的中点,点沿从点运动到点,设,两点间的距离为,,图2是点运动时随变化的关系图象,则的长为( )
A. B. C. D.
二、填空题(32分)
11. 如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为 .
12.如图所示,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为 .
13.如图,作一个以数轴的原点为圆心,长方形对角线为半径的圆弧,交数轴于点A,则点A表示的数是 .
14.如图,一架梯子AB长10米,底端离墙的距离BC为6米,当梯子下滑到DE时,AD=2米,则BE= 米.
15.如图,由四个全等的直角三角形拼成“赵爽弦图”.Rt△ABF中,∠AFB=90°,AF=4,AB=5.四边形EFGH的面积是 .
16. 如图,△ABC中,AB=AC=4,∠BAC=45°,AM平分∠BAC,点D、E 分别为AM、AB上的动点,则BD+DE的最小值是 .
17.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线交于点.若,则__________.
18. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=10,D是BC的中点,E是AC上一动点,将△CDE沿DE折叠到△C'DE,连接AC',当△AEC'是直角三角形时,CE的长为 .
三、解答题(48分)。
19. .如图所示,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.
20. 如图,在△ABC中,∠ACB=90°,,.
(1)求AB的长度;
(2)已知D是AB上一点,连接CD,当CD的长度最短时,求AD的长度.
21. 如图,在Rt△ABC中,∠C=90°,AC=8,在△ABE中,DE是AB边上的高,DE=8,S△ABE=40.求BC的长度.
22. 如图,一辆小汽车在一条限速40km/h的街路上沿直道行驶,某一时刻刚好行驶到路面车速检测仪A的正前方60m处的C点,过了8s后,测得小汽车所在的B点与车速检测仪A之间的距离为100m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.
23. 在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
24.【图形定义】
我们把对角线互相垂直的四边形叫做垂美四边形.
【性质探究】
如图1,四边形ABCD是垂美四边形,试探究两组对边AB,CD与BC,AD之间的数量关系,并证明你的结论;
【拓展应用】
如图2,Rt△ACB中,∠ACB=90°,分别以AC和AB为直角边向外作等腰Rt△ACD和等腰Rt△ABE,连接DE,若AC=4,AB=5,求DE的长.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
