第一章 丰富的图形世界 单元复习题 2022--2023学年北师大版七年级数学上册(含解析)
文档属性
| 名称 | 第一章 丰富的图形世界 单元复习题 2022--2023学年北师大版七年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 183.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 16:26:45 | ||
图片预览



文档简介
北师大版七年级数学上册第一章丰富的图形世界单元复习题
一、选择题
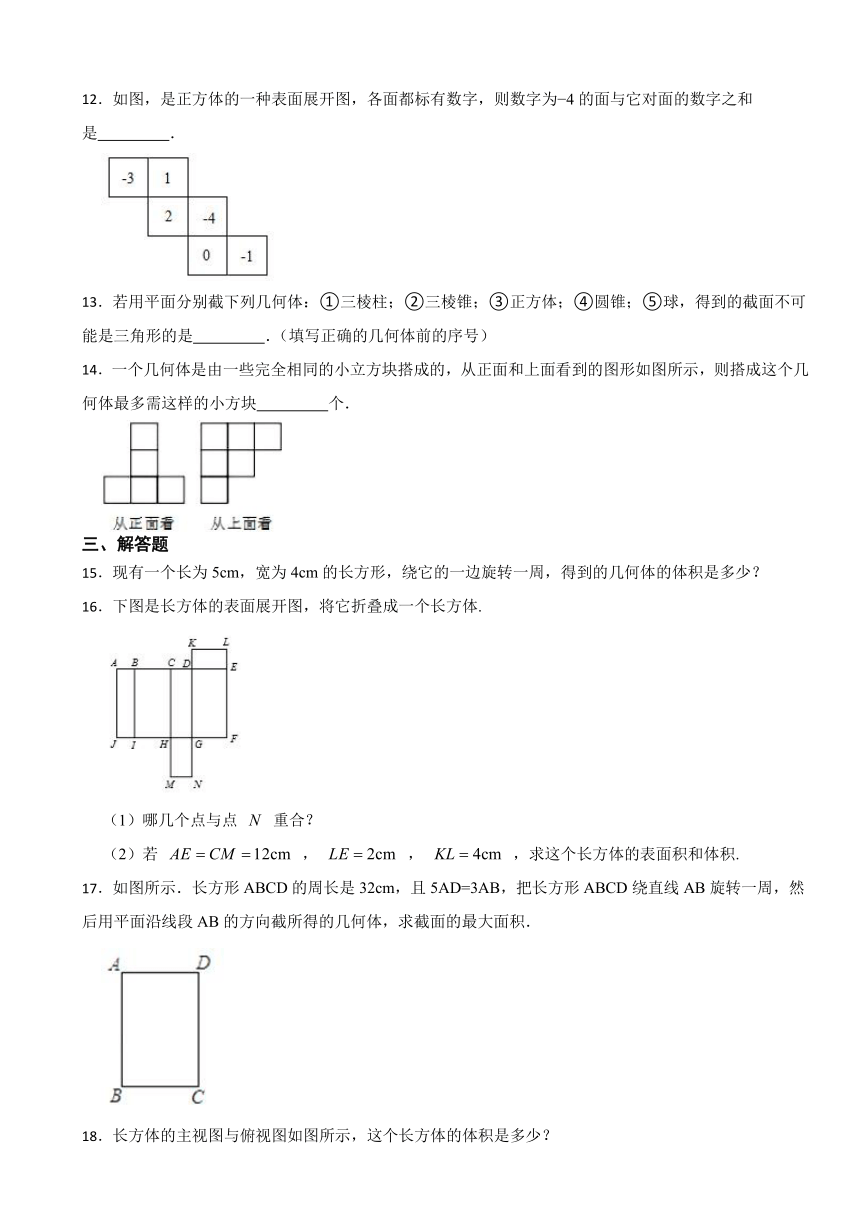
1.下列几何体中棱柱的个数为( )
A.4个 B.2个 C.3个 D.1个
2.下图是( )的展开图.
A.棱柱 B.棱锥 C.圆柱 D.圆锥
3.在一个正方体玻璃容器内装一些水,把容器按不同方式倾斜,容器内水面的形状不可能是( )
A. B.
C. D.
4.如图,由一个球体和一个长方体组成的几何体,从它的正面看得到的平面图形是( )
A. B.
C. D.
5.下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )
A.直角三角形 B.等腰三角形 C.矩形 D.扇形
6.“十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( )
A.圆锥 B.圆柱 C.球 D.圆台
7.如图,是正方体的展开图的有( )
A.1个 B.2个 C.3个 D.4个
8.用一个平面去截一个三棱柱,不能得到的截面形状是( )
A.等边三角形 B.长方形 C.梯形 D.六边形
9.用一平面去截下列几何体,其截面可能是长方形的有( )
A.1个 B.2个 C.3个 D.4个
10.如图是由6个小正方体拼成的几何体,该几何体从上面看到的形状图是( )
A. B.
C. D.
二、填空题
11.一个棱柱有10个面,则这个棱柱的底面是 边形.
12.如图,是正方体的一种表面展开图,各面都标有数字,则数字为 4的面与它对面的数字之和是 .
13.若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,得到的截面不可能是三角形的是 .(填写正确的几何体前的序号)
14.一个几何体是由一些完全相同的小立方块搭成的,从正面和上面看到的图形如图所示,则搭成这个几何体最多需这样的小方块 个.
三、解答题
15.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,得到的几何体的体积是多少?
16.下图是长方体的表面展开图,将它折叠成一个长方体.
(1)哪几个点与点 重合?
(2)若 , , ,求这个长方体的表面积和体积.
17.如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.
18.长方体的主视图与俯视图如图所示,这个长方体的体积是多少?
四、综合题
19.已知一直棱柱共有11个面,且它的底面边长都相等,侧棱长是10厘米,侧面积是180平方厘米.
(1)它是几棱柱?
(2)它的底面边长是多少?
20.如图是一个食品包装盒的表面展开图.
(1)写出这个包装盒形状的几何名称;
(2)求这个包装盒的表面积.
21.从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件,求:
(1)这个零件的表面积(包括底面);
(2)这个零件的体积.
22.已知如图是从三个方向看到的一个几何体的形状.
(1)写出这个几何体的名称:
(2)若从正面看到的高为10cm,从上面看到的三角形的三边长都为4cm,求这个几何体的侧面积.
答案解析部分
1.【答案】B
【解析】【解答】解:根据棱柱的定义可知:①是四棱柱,③是三棱柱,其余的均不是棱柱,
故棱柱有个.
故答案为:B.
【分析】有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,据此判断.
2.【答案】C
【解析】【解答】解:展开图中上下底面是圆,中间是长方形,符合圆柱的展开图.
故答案为:C
【分析】根据展开图中上下底面是圆,侧面是长方形即可判断.
3.【答案】D
【解析】【解答】解:根据题意,结合实际,容器内水面的形状不可能是七边形.
故答案为:D.
【分析】 在一个正方体玻璃容器内装一些水,把容器按不同方式倾斜,容器内水面的形状最多是六边形,据此判断即可.
4.【答案】B
【解析】【解答】解:从正面看,底层是一个矩形,上层中间是一个圆.
故答案为:B.
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
5.【答案】B
【解析】【解答】解:沿着某一直线旋转180°后,一定能形成圆锥的是等腰三角形.
故答案为:B.
【分析】等腰三角形沿着底边上的高旋转一周可得到圆锥,据此判断.
6.【答案】C
【解析】【解答】当硬币在地面某位置快速旋转时,形成的几何体是球,
故答案为:C.
【分析】根据面动成体,故硬币在地面某位置旋转时,形成球体。
7.【答案】B
【解析】【解答】解:由正方体展开图的特征可知,从左数第3、4个图形可以拼成一个正方体,第1个图形有两个面重复,第2个图形是凹字格,故不是正方体的展开图.
∴正方体的展开图的有2个.
故答案为:B.
【分析】正方体展开图的类型:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形;“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连);“2—2—2”型。其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形;“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形.
8.【答案】D
【解析】【解答】解:用平面去截一个三棱柱,其截面的形状有四种:长方形,梯形,三角形,五边形,不可能是六边形,
故答案为:D.
【分析】根据平面截三棱柱的不同角度与位置判断相应截面形状即可。
9.【答案】C
【解析】【解答】解:圆锥、圆台不可能得到长方形截面,
能得到长方形截面的几何体有:圆柱、长方体、四棱柱一共有3个.
故答案为:C.
【分析】圆柱可以截出4种截面:有圆形、长方形、类似于梯形但不是梯形、椭圆形;
长方体的截面:三角形、四边形、五边形、六边形;
圆锥的截面:抛物线 、椭圆形 、双曲线;
四棱柱的截面:三角形、四边形、五边形、六边形;
圆台的截面:圆、等腰梯形.
10.【答案】D
【解析】【解答】解:由题意可知该几何体从上面看到的形状图是,
故答案为:D.
【分析】从上面看所得的平面图形有2层,上层有3个小正方形,下层最右边有1个正方形,据此判断.
11.【答案】八
【解析】【解答】解: 一个棱柱有10个面,则这个棱柱的底面是八边形.
故答案为:八.
【分析】n棱柱,有2n个顶点,n条侧棱,n个侧面,据此得出一个棱柱有10个面,其中8个侧面,即可得出答案.
12.【答案】-7
【解析】【解答】解:由图可知:
-4与-3相对,
∴-4+(-3)=-7,
故答案为:-7.
【分析】根据正方体展开图的规律求解即可。
13.【答案】⑤
【解析】【解答】解:①用平面截三棱柱时,可以得到三角形截面.
②当平面平行于三棱锥的任意面时,得到的截面都是三角形.
③当平面经过正方体的三个顶点时,所得到的截面为三角形.
④当平面沿着母线截圆锥时,可以得到三角形截面.
⑤用平面球时,无论什么方向截取圆柱都不会截得三角形.
故答案为∶⑤.
【分析】当截面的角度和方向不同时,球的截面无论什么方向截取球都不会截得三角形。
14.【答案】10
【解析】【解答】解:综合主视图和俯视图,
可知底层可有6个正方体,第二层可有2个正方体,第三层可有2个正方体,
所以搭成这个几何体最多需小立方块10个.
故答案为:10.
【分析】利用三视图的定义求解即可。
15.【答案】解:以宽为旋转轴,V=π×52×4=100π;
以长为旋转轴,V=π×42×5=80π
【解析】【分析】根据面运动成体得出将长方形的一边旋转一周应该是一个圆柱,此题两种情况: 情况①以长为4的边旋转一周,所得圆柱的高就是4,底面圆的半径是5,根据圆柱的体积公式即可算出答案;情况②以长为5的边旋转一周,所得圆柱的高就是5,底面圆的半径是4,根据圆柱的体积公式即可算出答案;
16.【答案】解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
( )若 , , ,求这个长方体的表面积和体积.
解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
【解析】【分析】(1)观察图形的特征,GF和GN是对应的边,MN和JI也是对应的边,从而可判断与字母N重合的点;(2)由 , , ,可得CH=CM-LK=12-4=8cm,再根据长方体的表面积和体积公式计算即可.
17.【答案】解:设AD=x,AB=y.
根据题意得:
解得:x=6,y=10.
∴AD=6,AB=10.
∴圆柱体的直径为12,高为10.
∴截面的最大面积=12×10=120cm2.
【解析】【分析】先求得长方形ABCD的长和宽,长方形ABCD绕直线AB旋转一周得到一个圆柱体,沿线段AB的方向截所得的几何体其中轴截面最大.
18.【答案】解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,
因此这个长方体的长、宽、高分别为4、2、3,
因此这个长方体的体积为4×2×3=24.
答:这个长方体的体积是24.
【解析】【分析】由所给的视图判断出长方体的长、宽、高,让它们相乘即可得到体积.
19.【答案】(1)解:∵11﹣2=9,
∴棱柱有9个侧面,为9棱柱.
(2)解:侧面积是180平方厘米,
所以每个侧面积为:180÷9=20平方厘米,
∴底边长为20÷10=2(厘米),
即此棱柱的底边长是2厘米.
【解析】【分析】(1)根据棱柱的特征求解即可;
(2)先求出每个侧面的面积,再根据矩形的面积可得底边长为20÷10=2,从而得解。
20.【答案】(1)解:由食品包装盒的表面展开图可得,这个包装盒形状是长方体.
(2)解:由展开图可知,
长方体的表面积为2×6×4+2×2×2=56(dm2).
【解析】【分析】(1)根据所给的表面展开图求解即可;
(2)利用长方体的表面积公式计算求解即可。
21.【答案】(1)解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,则表面积是2×2×6=24
(2)解:23﹣13=8﹣1=7
【解析】【分析】(1)用平移的观点来看,从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件其表面积应该是原正方体的表面积,根据正方体的表面积等于一个面的面积乘以6,即可得出答案;
(2)该正方体的体积是原正方体的体积减去边长为1的小正方体的体积。
22.【答案】(1)解:由几何体的三视图可知,这个几何体是三棱柱;
(2)解:该几何体的侧面是三个边长为4cm和10cm的长方形,
∴这个几何体的侧面积为:4×10×3=120(cm2).
【解析】【分析】(1)根据三视图的定义求解即可;
(2)先求出该几何体的侧面是三个边长为4cm和10cm的长方形,再利用面积公式计算即可。
一、选择题
1.下列几何体中棱柱的个数为( )
A.4个 B.2个 C.3个 D.1个
2.下图是( )的展开图.
A.棱柱 B.棱锥 C.圆柱 D.圆锥
3.在一个正方体玻璃容器内装一些水,把容器按不同方式倾斜,容器内水面的形状不可能是( )
A. B.
C. D.
4.如图,由一个球体和一个长方体组成的几何体,从它的正面看得到的平面图形是( )
A. B.
C. D.
5.下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )
A.直角三角形 B.等腰三角形 C.矩形 D.扇形
6.“十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( )
A.圆锥 B.圆柱 C.球 D.圆台
7.如图,是正方体的展开图的有( )
A.1个 B.2个 C.3个 D.4个
8.用一个平面去截一个三棱柱,不能得到的截面形状是( )
A.等边三角形 B.长方形 C.梯形 D.六边形
9.用一平面去截下列几何体,其截面可能是长方形的有( )
A.1个 B.2个 C.3个 D.4个
10.如图是由6个小正方体拼成的几何体,该几何体从上面看到的形状图是( )
A. B.
C. D.
二、填空题
11.一个棱柱有10个面,则这个棱柱的底面是 边形.
12.如图,是正方体的一种表面展开图,各面都标有数字,则数字为 4的面与它对面的数字之和是 .
13.若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,得到的截面不可能是三角形的是 .(填写正确的几何体前的序号)
14.一个几何体是由一些完全相同的小立方块搭成的,从正面和上面看到的图形如图所示,则搭成这个几何体最多需这样的小方块 个.
三、解答题
15.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,得到的几何体的体积是多少?
16.下图是长方体的表面展开图,将它折叠成一个长方体.
(1)哪几个点与点 重合?
(2)若 , , ,求这个长方体的表面积和体积.
17.如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.
18.长方体的主视图与俯视图如图所示,这个长方体的体积是多少?
四、综合题
19.已知一直棱柱共有11个面,且它的底面边长都相等,侧棱长是10厘米,侧面积是180平方厘米.
(1)它是几棱柱?
(2)它的底面边长是多少?
20.如图是一个食品包装盒的表面展开图.
(1)写出这个包装盒形状的几何名称;
(2)求这个包装盒的表面积.
21.从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件,求:
(1)这个零件的表面积(包括底面);
(2)这个零件的体积.
22.已知如图是从三个方向看到的一个几何体的形状.
(1)写出这个几何体的名称:
(2)若从正面看到的高为10cm,从上面看到的三角形的三边长都为4cm,求这个几何体的侧面积.
答案解析部分
1.【答案】B
【解析】【解答】解:根据棱柱的定义可知:①是四棱柱,③是三棱柱,其余的均不是棱柱,
故棱柱有个.
故答案为:B.
【分析】有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,据此判断.
2.【答案】C
【解析】【解答】解:展开图中上下底面是圆,中间是长方形,符合圆柱的展开图.
故答案为:C
【分析】根据展开图中上下底面是圆,侧面是长方形即可判断.
3.【答案】D
【解析】【解答】解:根据题意,结合实际,容器内水面的形状不可能是七边形.
故答案为:D.
【分析】 在一个正方体玻璃容器内装一些水,把容器按不同方式倾斜,容器内水面的形状最多是六边形,据此判断即可.
4.【答案】B
【解析】【解答】解:从正面看,底层是一个矩形,上层中间是一个圆.
故答案为:B.
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
5.【答案】B
【解析】【解答】解:沿着某一直线旋转180°后,一定能形成圆锥的是等腰三角形.
故答案为:B.
【分析】等腰三角形沿着底边上的高旋转一周可得到圆锥,据此判断.
6.【答案】C
【解析】【解答】当硬币在地面某位置快速旋转时,形成的几何体是球,
故答案为:C.
【分析】根据面动成体,故硬币在地面某位置旋转时,形成球体。
7.【答案】B
【解析】【解答】解:由正方体展开图的特征可知,从左数第3、4个图形可以拼成一个正方体,第1个图形有两个面重复,第2个图形是凹字格,故不是正方体的展开图.
∴正方体的展开图的有2个.
故答案为:B.
【分析】正方体展开图的类型:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形;“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连);“2—2—2”型。其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形;“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形.
8.【答案】D
【解析】【解答】解:用平面去截一个三棱柱,其截面的形状有四种:长方形,梯形,三角形,五边形,不可能是六边形,
故答案为:D.
【分析】根据平面截三棱柱的不同角度与位置判断相应截面形状即可。
9.【答案】C
【解析】【解答】解:圆锥、圆台不可能得到长方形截面,
能得到长方形截面的几何体有:圆柱、长方体、四棱柱一共有3个.
故答案为:C.
【分析】圆柱可以截出4种截面:有圆形、长方形、类似于梯形但不是梯形、椭圆形;
长方体的截面:三角形、四边形、五边形、六边形;
圆锥的截面:抛物线 、椭圆形 、双曲线;
四棱柱的截面:三角形、四边形、五边形、六边形;
圆台的截面:圆、等腰梯形.
10.【答案】D
【解析】【解答】解:由题意可知该几何体从上面看到的形状图是,
故答案为:D.
【分析】从上面看所得的平面图形有2层,上层有3个小正方形,下层最右边有1个正方形,据此判断.
11.【答案】八
【解析】【解答】解: 一个棱柱有10个面,则这个棱柱的底面是八边形.
故答案为:八.
【分析】n棱柱,有2n个顶点,n条侧棱,n个侧面,据此得出一个棱柱有10个面,其中8个侧面,即可得出答案.
12.【答案】-7
【解析】【解答】解:由图可知:
-4与-3相对,
∴-4+(-3)=-7,
故答案为:-7.
【分析】根据正方体展开图的规律求解即可。
13.【答案】⑤
【解析】【解答】解:①用平面截三棱柱时,可以得到三角形截面.
②当平面平行于三棱锥的任意面时,得到的截面都是三角形.
③当平面经过正方体的三个顶点时,所得到的截面为三角形.
④当平面沿着母线截圆锥时,可以得到三角形截面.
⑤用平面球时,无论什么方向截取圆柱都不会截得三角形.
故答案为∶⑤.
【分析】当截面的角度和方向不同时,球的截面无论什么方向截取球都不会截得三角形。
14.【答案】10
【解析】【解答】解:综合主视图和俯视图,
可知底层可有6个正方体,第二层可有2个正方体,第三层可有2个正方体,
所以搭成这个几何体最多需小立方块10个.
故答案为:10.
【分析】利用三视图的定义求解即可。
15.【答案】解:以宽为旋转轴,V=π×52×4=100π;
以长为旋转轴,V=π×42×5=80π
【解析】【分析】根据面运动成体得出将长方形的一边旋转一周应该是一个圆柱,此题两种情况: 情况①以长为4的边旋转一周,所得圆柱的高就是4,底面圆的半径是5,根据圆柱的体积公式即可算出答案;情况②以长为5的边旋转一周,所得圆柱的高就是5,底面圆的半径是4,根据圆柱的体积公式即可算出答案;
16.【答案】解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
( )若 , , ,求这个长方体的表面积和体积.
解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
【解析】【分析】(1)观察图形的特征,GF和GN是对应的边,MN和JI也是对应的边,从而可判断与字母N重合的点;(2)由 , , ,可得CH=CM-LK=12-4=8cm,再根据长方体的表面积和体积公式计算即可.
17.【答案】解:设AD=x,AB=y.
根据题意得:
解得:x=6,y=10.
∴AD=6,AB=10.
∴圆柱体的直径为12,高为10.
∴截面的最大面积=12×10=120cm2.
【解析】【分析】先求得长方形ABCD的长和宽,长方形ABCD绕直线AB旋转一周得到一个圆柱体,沿线段AB的方向截所得的几何体其中轴截面最大.
18.【答案】解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,
因此这个长方体的长、宽、高分别为4、2、3,
因此这个长方体的体积为4×2×3=24.
答:这个长方体的体积是24.
【解析】【分析】由所给的视图判断出长方体的长、宽、高,让它们相乘即可得到体积.
19.【答案】(1)解:∵11﹣2=9,
∴棱柱有9个侧面,为9棱柱.
(2)解:侧面积是180平方厘米,
所以每个侧面积为:180÷9=20平方厘米,
∴底边长为20÷10=2(厘米),
即此棱柱的底边长是2厘米.
【解析】【分析】(1)根据棱柱的特征求解即可;
(2)先求出每个侧面的面积,再根据矩形的面积可得底边长为20÷10=2,从而得解。
20.【答案】(1)解:由食品包装盒的表面展开图可得,这个包装盒形状是长方体.
(2)解:由展开图可知,
长方体的表面积为2×6×4+2×2×2=56(dm2).
【解析】【分析】(1)根据所给的表面展开图求解即可;
(2)利用长方体的表面积公式计算求解即可。
21.【答案】(1)解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,则表面积是2×2×6=24
(2)解:23﹣13=8﹣1=7
【解析】【分析】(1)用平移的观点来看,从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,得到一个如图的零件其表面积应该是原正方体的表面积,根据正方体的表面积等于一个面的面积乘以6,即可得出答案;
(2)该正方体的体积是原正方体的体积减去边长为1的小正方体的体积。
22.【答案】(1)解:由几何体的三视图可知,这个几何体是三棱柱;
(2)解:该几何体的侧面是三个边长为4cm和10cm的长方形,
∴这个几何体的侧面积为:4×10×3=120(cm2).
【解析】【分析】(1)根据三视图的定义求解即可;
(2)先求出该几何体的侧面是三个边长为4cm和10cm的长方形,再利用面积公式计算即可。
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
