新人教版4年级上册 1.7 数的产生 教学课件(41张PPT)
文档属性
| 名称 | 新人教版4年级上册 1.7 数的产生 教学课件(41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 44.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 00:00:00 | ||
图片预览







文档简介
(共41张PPT)
1.7 数的产生
第一单元 大数的认识
新人教版四年级上册
教学目标
1、通过经历原始人记数的过程,了解自然数产生的背景,感受“一一对应”的思想,简单介绍数的发展历史,课前自学了解四大文明古国的记数法,体会数的符号化和
优化的必要性,感受古人的智慧。
2、了解中国,罗马数的不同表示法,在中国算筹的发展演变过程中让学生体会十进制
位值制的先进和方便,了解0的发展历史及占位思想。
3、介绍阿拉伯数的发展演变历史,让学生在优胜劣汰的过程中体会数学优化思想。
4、通过学生推理,猜想,验证各类古人记数法,激发学生的数学兴趣和民族自豪感,体会和感受人类伟大的创造力。
我们身边有很多数,找一找。
我们的生活离不开数,可是数的产生也经历了一个漫长的过程。
四年级
9岁
10岁
2019年
全班31人
身高143厘米
体重45千克
全校大约500人
学号01号
……
课前导入
古时候,人们在生产劳动中,逐渐有了计数的需要。
探究新知
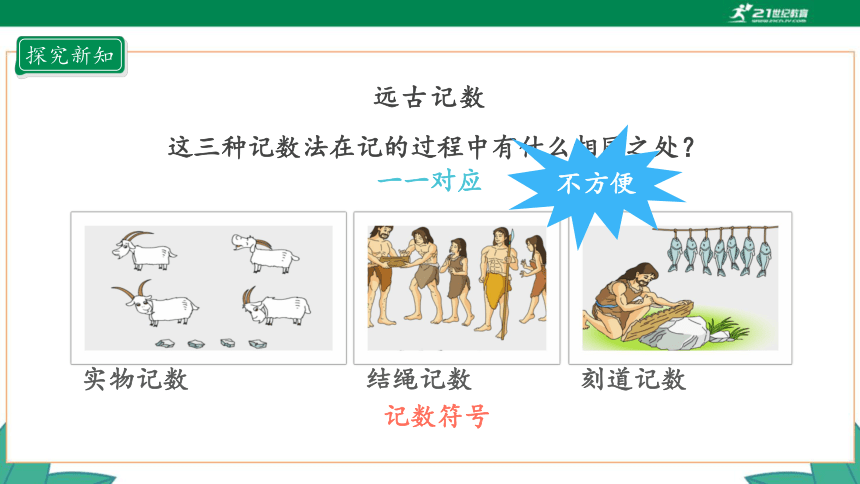
实物记数
结绳记数
刻道记数
远古记数
这三种记数法在记的过程中有什么相同之处?
一一对应
不方便
记数符号
探究新知
远古记数
如果你是原古人,你能想到怎样的记数符号呢?
圆圈和正方形,还有三角形之类的
画正字
画树枝
用倒着的三角形表示一,用横着的三角形表示十
探究新知
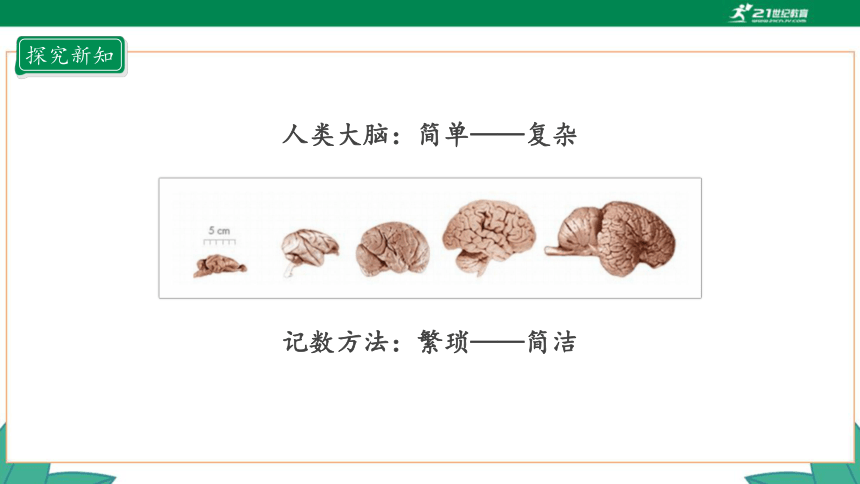
人类大脑:简单——复杂
记数方法:繁琐——简洁
探究新知
探究新知
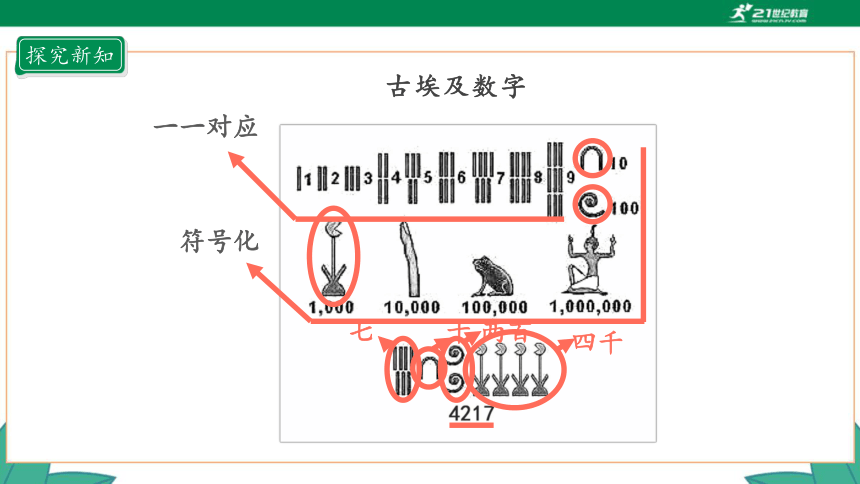
一一对应
符号化
四千
两百
十
七
古埃及数字
探究新知
古巴比伦数字
一一对应
两个十,三个十,四个十,五个十
六十进制法
探究新知
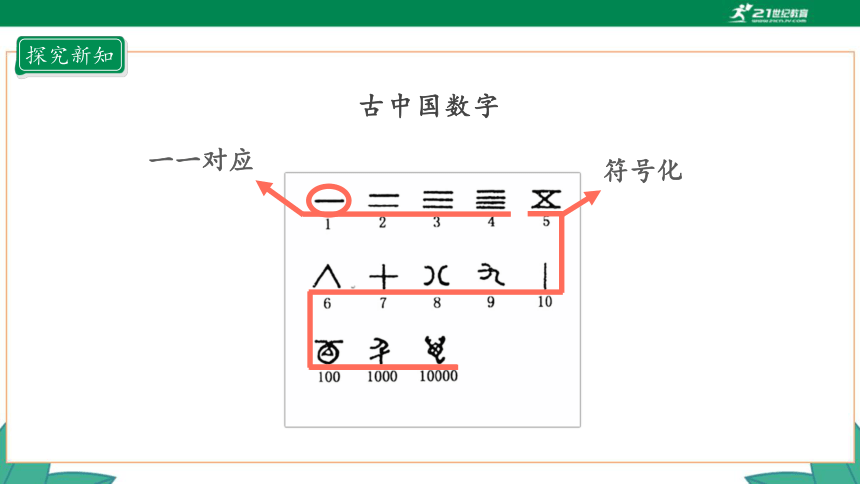
古中国数字
一一对应
符号化
探究新知
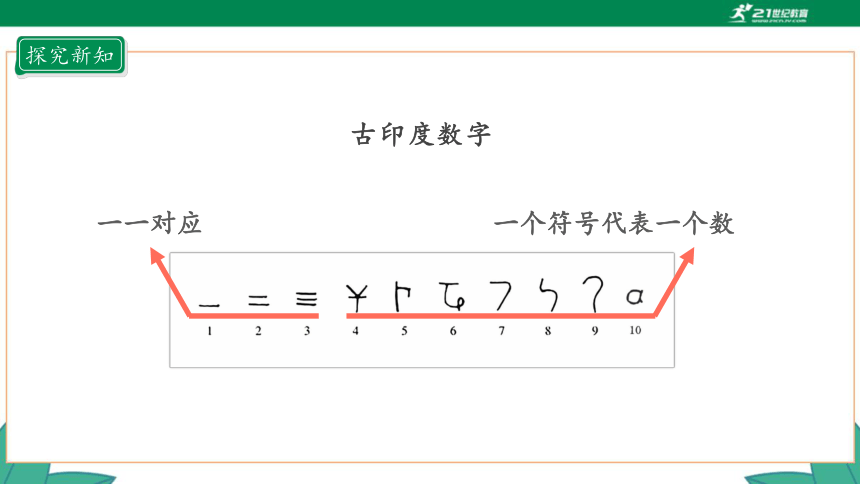
古印度数字
一一对应
一个符号代表一个数
探究新知
古印度数字
古埃及数字
古巴比伦数字
古中国数字
稍微简单了
慢慢符号化
优化
进步:
问题:
繁琐
认不清
探究新知
中国算筹:
罗马数:
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
6
I 代表1,—代表5
4
5
6
左减右加
IV=V-I
VI=V+I
VII=V+II
VIII=V+III
中国:
罗马:
10
X
IX=X-I
=10
X
代表10
满十向前一位进一
XI
11
LXXI
71
L=50
L=100
120
7个字母 I V X L C D M
1 5 10 50 100 500 1000
71
探究新知
罗马数:
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
左减右加
7个字母 I V X L C D M
1 5 10 50 100 500 1000
运算的方法
探究新知
中国算筹:
10
11
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
21
31
41
51
61
71
81
91
92
93
94
95
96
97
98
99
十位上都是一样:
右边:
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
100
99
+1 =
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
100
混淆
10
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
一根算筹还可以表示几?有什么发现?
还可以表示一千、一万、十万
放在不同的数位上,得到的数就不一样
还可以表示无数个数
越来越像我们现在的表示形式了
探究新知
数级 亿级 万级 个级 数位 … 亿 位 千万位 百万位 十万位 万位 千位 百位 十位 个位
计数单位 …
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
个
十
百
千
万
十万
百万
千万
亿
10
10
10
10
10
10
10
10
十进制
算筹放在不同的数位上,得到的数就不一样
位值制
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
五根算筹可以表示几?
90
50
90
63
72
9
81
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
五根算筹可以表示几?
5
203
8001
810
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
五根算筹可以表示几?
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
对比各个国家的记数符号,中国算筹有什么优点?
十进制
位值制
探究新知
我国在商代的文字记数中就已经有了十进位值制的萌芽,而2000多年前中国古代十进位值制的算筹记数法在世界数学史上更是一个伟大的创造。
各个地区的数字不同,交流起来很不方便。
一而十 十而百
百而千 千而万
探究新知
各个地区的数字不同,交流起来很不方便。
统一
该使用哪个国家的
阿拉伯数字
印度人
探究新知
探究新知
阿拉伯数字
探究新知
2个苹果
30支铅笔
表示物体的个数
表示物体排列的顺序
小红排第5,小明排第7
探究新知
探究新知
表示物体个数的1、2、3、4、5、6、7、8、9、10、11…都是自然数。
0是不是自然数?
探究新知
306
中国数字:
探究新知
探究新知
表示物体个数的1、2、3、4、5、6、7、8、9、10、11…都是自然数。
“一个物体也没有,用0表示”,0也是自然数。所有的自然数都是整数
探究新知
1.这些自然数是怎么排列的?
2.每相邻两个自然数相差几?
3.最小的自然数是几?
4.有没有最大的自然数
5..自然数有多少个?
从小到大或者从大到小排列
相差1
0
没有
自然数的个数是无限的
自然数的特点
1.判断:
(1)“阿拉伯数字”是阿拉伯人发明的。 ( )
印度人
(2)判断:自然数的个数是无限的。 ( )
1
1
1
1
1
1
一个一个地数,总也数不完,数出一个很大很大的数以后,还可以数出一个比它多1的大数。
巩固提升
(2)相邻的两个自然数的差是______。
2.填空。
1
1
1
1
1
1
0 1 2 3 4 5 6 7 8 9 10 11 …
1
(1)最小的自然数是______,
自然数的个数是______的。
0
无限
巩固提升
(3)与1000相邻的两个自然数分别是______和______。
1000+1=1001
1000-1=999
1001
999
相邻的两个自然数相差1。
巩固提升
某校学生数是一个四位数,个位上的数字比百位上的数字多1,百位上的数字是十位上的数字的4倍,千位上的数字是百位上的数字的一半,这个数比4000大,比5000小,这个数是多少?
4
千 百 十 个
8
2
9
答:这个数是4829。
巩固提升
数的产生
这节课有什么收获呢?
课堂小结
自然数
表示物体个数的1,2,3,4,5,6,7,8,9,10,11…都是自然数。
最小的自然数是0,没有最大的自然数。自然数的个数是无限的。
概 念:
特 点:
课堂小结
结绳计数这种方法,不但在远古时候使用,而且一直在某些民族中沿用下来。
宋朝人在一本书中说:“鞑靼无文字,每调发军马,即结草为约,使人传达,急于星火。”这是用结草来调发军马,传达要调的人数呢!其他如藏族、彝族等,虽都有文字,但在一般不识字的人中间都还长期使用这种方法。
结 绳 计 数
课堂小结
1.7 数的产生
第一单元 大数的认识
新人教版四年级上册
教学目标
1、通过经历原始人记数的过程,了解自然数产生的背景,感受“一一对应”的思想,简单介绍数的发展历史,课前自学了解四大文明古国的记数法,体会数的符号化和
优化的必要性,感受古人的智慧。
2、了解中国,罗马数的不同表示法,在中国算筹的发展演变过程中让学生体会十进制
位值制的先进和方便,了解0的发展历史及占位思想。
3、介绍阿拉伯数的发展演变历史,让学生在优胜劣汰的过程中体会数学优化思想。
4、通过学生推理,猜想,验证各类古人记数法,激发学生的数学兴趣和民族自豪感,体会和感受人类伟大的创造力。
我们身边有很多数,找一找。
我们的生活离不开数,可是数的产生也经历了一个漫长的过程。
四年级
9岁
10岁
2019年
全班31人
身高143厘米
体重45千克
全校大约500人
学号01号
……
课前导入
古时候,人们在生产劳动中,逐渐有了计数的需要。
探究新知
实物记数
结绳记数
刻道记数
远古记数
这三种记数法在记的过程中有什么相同之处?
一一对应
不方便
记数符号
探究新知
远古记数
如果你是原古人,你能想到怎样的记数符号呢?
圆圈和正方形,还有三角形之类的
画正字
画树枝
用倒着的三角形表示一,用横着的三角形表示十
探究新知
人类大脑:简单——复杂
记数方法:繁琐——简洁
探究新知
探究新知
一一对应
符号化
四千
两百
十
七
古埃及数字
探究新知
古巴比伦数字
一一对应
两个十,三个十,四个十,五个十
六十进制法
探究新知
古中国数字
一一对应
符号化
探究新知
古印度数字
一一对应
一个符号代表一个数
探究新知
古印度数字
古埃及数字
古巴比伦数字
古中国数字
稍微简单了
慢慢符号化
优化
进步:
问题:
繁琐
认不清
探究新知
中国算筹:
罗马数:
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
6
I 代表1,—代表5
4
5
6
左减右加
IV=V-I
VI=V+I
VII=V+II
VIII=V+III
中国:
罗马:
10
X
IX=X-I
=10
X
代表10
满十向前一位进一
XI
11
LXXI
71
L=50
L=100
120
7个字母 I V X L C D M
1 5 10 50 100 500 1000
71
探究新知
罗马数:
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ
左减右加
7个字母 I V X L C D M
1 5 10 50 100 500 1000
运算的方法
探究新知
中国算筹:
10
11
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
21
31
41
51
61
71
81
91
92
93
94
95
96
97
98
99
十位上都是一样:
右边:
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
100
99
+1 =
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
100
混淆
10
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
一根算筹还可以表示几?有什么发现?
还可以表示一千、一万、十万
放在不同的数位上,得到的数就不一样
还可以表示无数个数
越来越像我们现在的表示形式了
探究新知
数级 亿级 万级 个级 数位 … 亿 位 千万位 百万位 十万位 万位 千位 百位 十位 个位
计数单位 …
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
个
十
百
千
万
十万
百万
千万
亿
10
10
10
10
10
10
10
10
十进制
算筹放在不同的数位上,得到的数就不一样
位值制
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
五根算筹可以表示几?
90
50
90
63
72
9
81
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
五根算筹可以表示几?
5
203
8001
810
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
五根算筹可以表示几?
探究新知
中国算筹:
(9个数码在各个数位上横纵交错)
纵式(个位、百位、万位)
1 2 3 4 5 6 7 8 9
横式(十位、千位、十万位)
1 2 3 4 5 6 7 8 9
对比各个国家的记数符号,中国算筹有什么优点?
十进制
位值制
探究新知
我国在商代的文字记数中就已经有了十进位值制的萌芽,而2000多年前中国古代十进位值制的算筹记数法在世界数学史上更是一个伟大的创造。
各个地区的数字不同,交流起来很不方便。
一而十 十而百
百而千 千而万
探究新知
各个地区的数字不同,交流起来很不方便。
统一
该使用哪个国家的
阿拉伯数字
印度人
探究新知
探究新知
阿拉伯数字
探究新知
2个苹果
30支铅笔
表示物体的个数
表示物体排列的顺序
小红排第5,小明排第7
探究新知
探究新知
表示物体个数的1、2、3、4、5、6、7、8、9、10、11…都是自然数。
0是不是自然数?
探究新知
306
中国数字:
探究新知
探究新知
表示物体个数的1、2、3、4、5、6、7、8、9、10、11…都是自然数。
“一个物体也没有,用0表示”,0也是自然数。所有的自然数都是整数
探究新知
1.这些自然数是怎么排列的?
2.每相邻两个自然数相差几?
3.最小的自然数是几?
4.有没有最大的自然数
5..自然数有多少个?
从小到大或者从大到小排列
相差1
0
没有
自然数的个数是无限的
自然数的特点
1.判断:
(1)“阿拉伯数字”是阿拉伯人发明的。 ( )
印度人
(2)判断:自然数的个数是无限的。 ( )
1
1
1
1
1
1
一个一个地数,总也数不完,数出一个很大很大的数以后,还可以数出一个比它多1的大数。
巩固提升
(2)相邻的两个自然数的差是______。
2.填空。
1
1
1
1
1
1
0 1 2 3 4 5 6 7 8 9 10 11 …
1
(1)最小的自然数是______,
自然数的个数是______的。
0
无限
巩固提升
(3)与1000相邻的两个自然数分别是______和______。
1000+1=1001
1000-1=999
1001
999
相邻的两个自然数相差1。
巩固提升
某校学生数是一个四位数,个位上的数字比百位上的数字多1,百位上的数字是十位上的数字的4倍,千位上的数字是百位上的数字的一半,这个数比4000大,比5000小,这个数是多少?
4
千 百 十 个
8
2
9
答:这个数是4829。
巩固提升
数的产生
这节课有什么收获呢?
课堂小结
自然数
表示物体个数的1,2,3,4,5,6,7,8,9,10,11…都是自然数。
最小的自然数是0,没有最大的自然数。自然数的个数是无限的。
概 念:
特 点:
课堂小结
结绳计数这种方法,不但在远古时候使用,而且一直在某些民族中沿用下来。
宋朝人在一本书中说:“鞑靼无文字,每调发军马,即结草为约,使人传达,急于星火。”这是用结草来调发军马,传达要调的人数呢!其他如藏族、彝族等,虽都有文字,但在一般不识字的人中间都还长期使用这种方法。
结 绳 计 数
课堂小结
