2023-2024学年福建省福州市台江区华伦中学七年级(上)入学分班数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年福建省福州市台江区华伦中学七年级(上)入学分班数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 114.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 21:28:11 | ||
图片预览



文档简介
2023-2024学年福州市台江区华伦中学七年级(上)入学分班
数学试卷
一、填空题(共28分)
1. ______ : ______ ______
2. 有一个点,它的位置定为,这个点先向上移动格,再向右移动格,则移动后这个点的位置可以表示为______ .
3. 盒子里有同样大小的红、黄、蓝、白四种颜色的球各个,要想摸出的球一定有个是同色的,最少要摸出______ 个球.
4. 阳光小学组织安全意识知识竞赛,共题,评分规则是答对一题得分,答错一题扣分,弃权不扣分也不得分,芳芳小组弃权两题,得了分,他们答对了______ 题
5. 如图,线段长为厘米一只蚂蚁从到沿着四个半圆爬行,蚂蚁的行程是______ 厘米.
6. 两位同学分别对同一个零件按照:和:的比例尺放大,结果图纸上两个零件的长度差厘米,那么这个零件的实际长度是______ 厘米.
7. 在如图中用阴影部分表示公顷.
8. 一个圆柱的底面半径和高相等,那么这个圆柱的底面积和侧面积的比是______ .
9. 旧书店按封底上的标价便宜收购旧书,然后按封底上的标价便宜卖出,旧书店可以获得的利润约是______
10. 五个连续自然数,其中第三个数比第一、第五两数和的少那么第三个数是______ .
11. 三条边长分别是厘米、厘米、厘米的直角三角形,将它的最短边对折与斜边相重合如图那么,图中阴影部分的面积是______ 平方厘米.
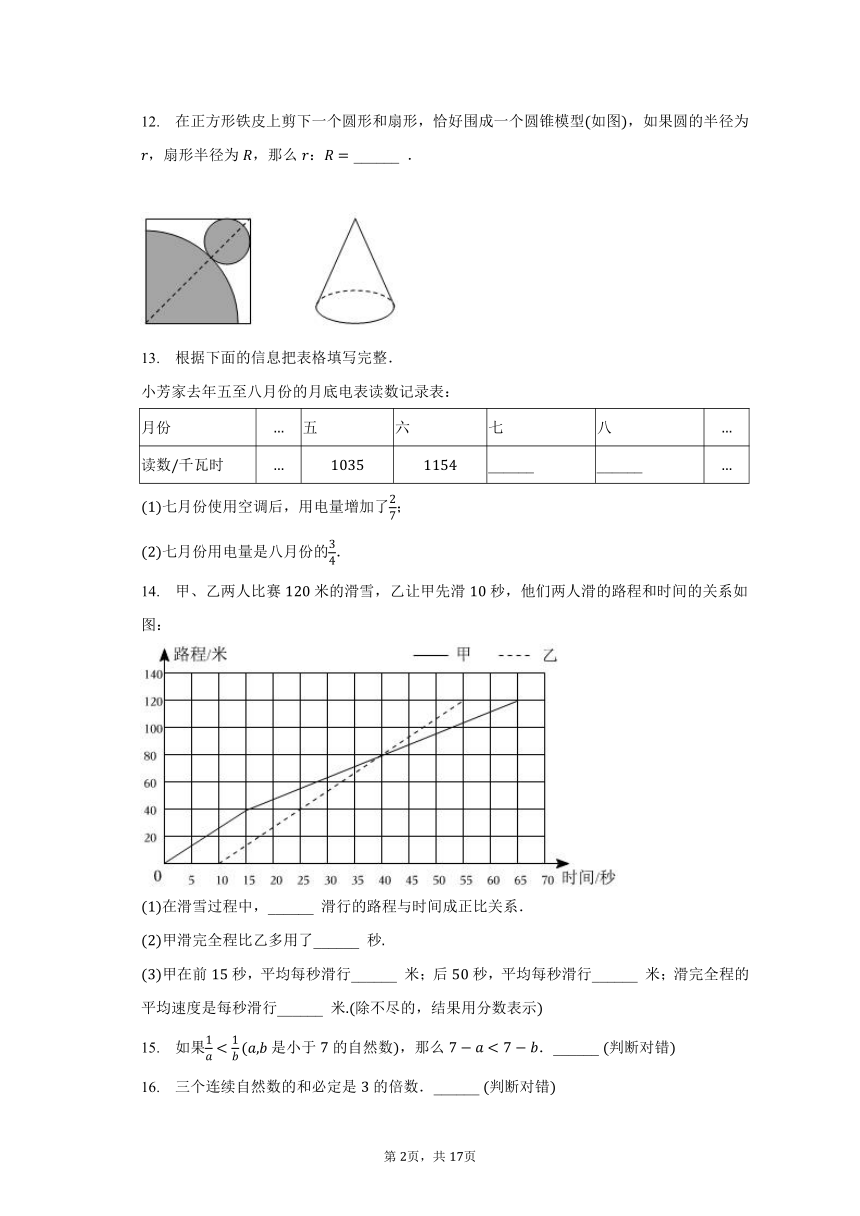
12. 在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型如图,如果圆的半径为,扇形半径为,那么: ______ .
13. 根据下面的信息把表格填写完整.
小芳家去年五至八月份的月底电表读数记录表:
月份 五 六 七 八
读数千瓦时 ______ ______
七月份使用空调后,用电量增加了;
七月份用电量是八月份的.
14. 甲、乙两人比赛米的滑雪,乙让甲先滑秒,他们两人滑的路程和时间的关系如图:
在滑雪过程中,______ 滑行的路程与时间成正比关系.
甲滑完全程比乙多用了______ 秒
甲在前秒,平均每秒滑行______ 米;后秒,平均每秒滑行______ 米;滑完全程的平均速度是每秒滑行______ 米除不尽的,结果用分数表示
15. 如果是小于的自然数,那么.______ 判断对错
16. 三个连续自然数的和必定是的倍数.______ 判断对错
17. 王师傅完成一项工作,由于工作效率提高了,故所用的时间节省了.______ 判断对错
18. 的积一定是,,的倍数是大于零的自然数 ______ 判断对错
19. 至少要加上它本身的,才能得到整数.______ 判断对错
二、选择题(本大题共5小题,共10分)
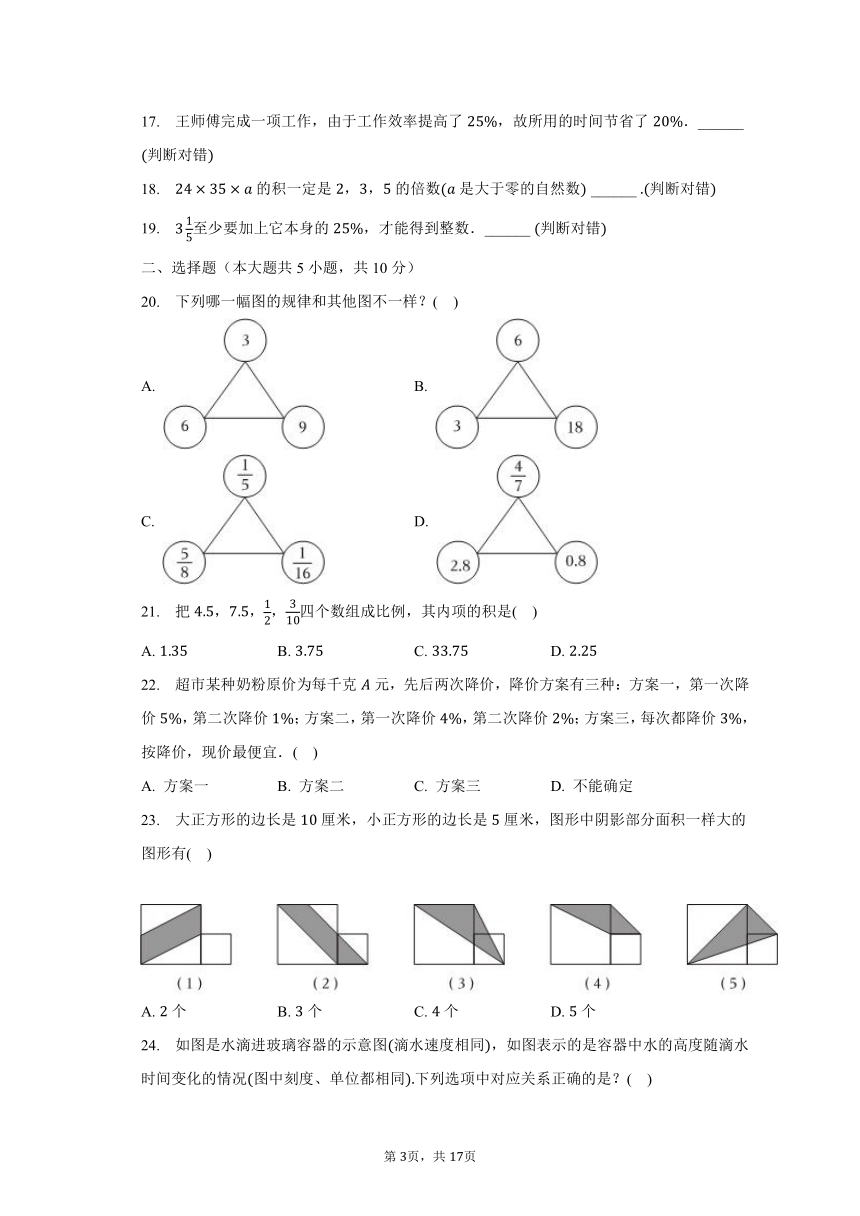
20. 下列哪一幅图的规律和其他图不一样?( )
A. B.
C. D.
21. 把,,,四个数组成比例,其内项的积是( )
A. B. C. D.
22. 超市某种奶粉原价为每千克元,先后两次降价,降价方案有三种:方案一,第一次降价,第二次降价;方案二,第一次降价,第二次降价;方案三,每次都降价,按降价,现价最便宜.( )
A. 方案一 B. 方案二 C. 方案三 D. 不能确定
23. 大正方形的边长是厘米,小正方形的边长是厘米,图形中阴影部分面积一样大的图形有( )
A. 个 B. 个 C. 个 D. 个
24. 如图是水滴进玻璃容器的示意图滴水速度相同,如图表示的是容器中水的高度随滴水时间变化的情况图中刻度、单位都相同下列选项中对应关系正确的是?( )
A. B. C. D.
三、解答题(共82分)
25. 用合理的方法计算:
;
;
26. 求未知数:
;
;
;
27. 小军班有多少人?小丽班有多少人?
小丽:我们班人数比你们班多.
小军:我们班比你们班少人.
28. “低碳生活”从现在做起,从我做起,据测算,公顷落叶阔叶林每年可吸收二氧化碳吨,如果每台空调制冷温度在国家提倡的摄氏度基础上调到摄氏度,相应每年减排二氧化碳千克某市仅此项就大约减排相当于公顷落叶阔叶林全年吸收的二氧化碳,若每个家庭按台空调计算,该市约有多少万户家庭?
29. 甲、乙两车分别从、两站出发相向而行,经过半小时后,甲车行驶了全程的乙车行驶了全程的,这时两车相距千米求、两站的距离.
答案和解析
1.【答案】
【解析】解:;
;
;
.
把小数化成百分数,把小数点向右移动两位,同时在后面加上百分号;把小数化成分数:原来有几位小数,就在的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分;分数化成不同的分数利用分数的基本性质求出即可.
本题考查百分数和分数、小数的互化.抓住之间的关系便可解决问题.
2.【答案】
【解析】解:根据有一个点,它的位置定为,点先向上移动格,行数增加格,列数不变即在,再向右移动格,行数不变,列数增加格,即.
故答案为:.
根据点的平移规律,进而得出答案.
此题主要考查了点的坐标,正确掌握点的平移规律是解题关键.
3.【答案】
【解析】解:根据题意得:
个,
最少要摸出个球.
故答案为:.
从最坏的情况考虑,假设每次摸到的颜色各不相同,则摸次可保证每种颜色的球各个,同理,摸次可保证每种颜色的球各个,再摸个,即可保证摸出的球一定有个是同色.
本题考查了利用抽屉原理解决实际问题,从最坏的情况考虑是解题的关键.
4.【答案】
【解析】解:设他们答对了道,则答错了道,
由题意可得:,
解得,
即他们答对了道题目,
故答案为:.
先设答对题目为道,则可以写出答错题目的道数,根据答对题目得分答错题目得分总得分,可以列出相应的方程,然后求解即可.
本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
5.【答案】
【解析】解:四个半圆弧长的和直径厘米的圆周长的一半,
厘米,
蚂蚁的行程是厘米.
故答案为:.
四个半圆弧长的和直径厘米的圆周长的一半,由圆周长公式即可求解.
本题考查圆的周长,关键是掌握圆周长公式.
6.【答案】
【解析】解:两位同学分别对同一个零件按照:和:的比例尺放大,结果图纸上两个零件的长度差厘米,
这个零件的实际长度是厘米.
故答案为:.
根据比例尺和已知条件得出这个零件的实际长度是,再求出答案即可.
本题考查了比例尺,能熟记比例尺是解此题的关键.
7.【答案】解:如图,阴影部分面积公顷.
【解析】由题意可得每个小长方形的面积为公顷,即可求解.
本题考查了作图基本作图,求出每个小长方形的面积是解题的关键.
8.【答案】:
【解析】解:设圆柱的底面半径和高都是,
则圆柱的底面积为,侧面积为,
这个圆柱的底面积和侧面积的比是::.
故答案为::.
设圆柱的底面半径和高都是,再分别求出圆柱的底面积和侧面积,即可求出答案.
本题主要考查了圆柱的计算,熟练掌握圆柱的底面积和侧面积的计算公式是解题关键.
9.【答案】
【解析】解:
.
答:旧书店可以获得的利润约是.
故答案为:.
根据利润率的意义可知:利润率利润成本;把封底上的标价看作是单位“”,根据利润率的意义进行解答即可.
本题考查了百分数的应用,掌握利润率计算公式”利润率利润成本“是解答本题的关键.
10.【答案】
【解析】解:设中间的一个自然数是,那么第一、五两数和是.
,
,
,
.
答:第三个数是.
故答案为:.
设中间的一个自然数是,因为是一个连续自然数,所以第一个自然数是,第二个自然数是,第四个自然数是,第五个自然数是,把第一、五两数加在一起求和,因为“中间的一个自然数,比第一、五两数和的少,据此等量关系可列方程求解.
解答此题先设出中间的自然数,再表示出其它的自然数,然后根据等量关系列出方程求解.
11.【答案】
【解析】解:如图:
由题意可知:,,,
,
:::,
:::,
平方厘米,
平方厘米,
故答案为:.
通过观察,原直角三角形被分成了三个直角三角形,依据题目条件可以先找出它们的面积比,总面积已知,进而得解.
此题主要考查等底等高的三角形面积相等,解答本题的关键是找准面积的比.
12.【答案】:
【解析】解:因为扇形的弧长等于圆锥底面周长,
所以,
所以
所以 ::;
故答案为::.
根据围成圆锥后圆锥的侧面展开扇形的弧长等于圆锥的底面周长,列出关系式即可得到两个半径之间的关系.
本题考查了圆锥的计算,解答此题的关键是明白:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.
13.【答案】
【解析】解:七月份的用电量为,
所以读数为;
故答案为:;
八月份的用电量为,
所以读数为;
故答案为:.
用六月份的用电量乘以求出七月份的用电量,即可得出答案;
用七月份的用电量除以求出八月份的用电量,即可得出答案.
本题考查了分数混合运算的应用,正确理解题意和准确计算是关键.
14.【答案】乙
【解析】解:由图可知,乙的图象是一条上升的直线,即成正比例关系,
乙滑行的路程与时间成正比关系,
答案为:乙;
甲第秒出发,第秒到终点;乙第秒时出发,第秒到达终点,
即甲全程用时秒,乙全程用时秒,
秒,
甲滑完全程比乙多用了秒,
答案为:;
米秒,
甲前秒速度为:米秒,
米秒,
后秒速度为:米秒,
米秒,
滑完全程的平均速度为:米秒.
答案为:,,.
由图可知,乙的图象是一条上升的直线,即成正比例关系;
甲第秒出发,第秒到终点;乙第秒时出发,第秒到达终点,即甲全程用时秒,乙全程用时秒,即可作答;
用速度路程时间,即可作答.
本题考查一次函数的应用,解题的关键是数形结合.
15.【答案】
【解析】解:是小于的自然数,
,
,故.
故答案为:.
根据是小于的自然数,可得,所以.
本题考查了整数的认识,熟练掌握分数的性质是关键.
16.【答案】对
【解析】解:对.
设三个连续的自然数中的第一个为,第二个为,第二个为.
其和为:,
三个连续的自然数的和,一定是的倍数.
设三个连续的正整数中的第一个为,第二个为,第二个为其和为:,由此即可得出结论.
本题考查的是整式的加减,熟知整式的加减实质上是合并同类项是解答此题的关键.
17.【答案】正确
【解析】解:现在的工作效率是原来的:,
原来的工作效率与现在的工作效率的比是:,
原来的工作时间:现在的工作时间::,
现在的工作时间是原来的,
时间节约了:,
原题说法是正确的.
故答案为:正确.
把原来的工作效率看成单位“”,现在的工作效率是原来的,原来的工作效率与现在的工作效率的比是:,而工作时间与工作效率成反比例,所以原来的工作时间:现在的工作时间:;根据这个比例求出现在的时间是原来的时间的几分之几,进而求出时间节约了百分之几.
本题考查了百分数的应用,解决本题先根据前后两次工作效率之间的比例关系找出它们所用的时间之间的比例关系,再根据求一个数是另一个数的百分之几的方法求解.
18.【答案】
【解析】解:,
是,,的倍数,
的积一定是,,的倍数是大于零的自然数.
故答案为:.
先求出的积,再根据,,的倍数的特征判断即可.
本题考查了倍数和整数的认识,掌握,,的倍数的特征是解答本题的关键.
19.【答案】
【解析】解:
.
所以题干的说法正确.
故答案为:.
把这个分数看作单位“”,比大的最小正整数为,求出两个数之间增加的百分率即可判断是否正确.
本题考查分数的混合运算,掌握分数化整数的方法便可解决问题.
20.【答案】
【解析】解:、;
B、;
C、;
D、.
图与其他图的规律不一样,
故选:.
根据图形中的数字找出规律:右边的数除以左边的数再乘以等于上边的数,从而得出结论.
本题考查图形变化类,关键是根据图形中的数字找出规律.
21.【答案】
【解析】解:,,
,
比例式为::,
两内项的积是.
故选:.
先求出比例式为::,再求出两内项和的积即可.
本题考查了比例的意义,能求出比例式::是解此题的关键.
22.【答案】
【解析】解:方案一、现价为:元,
方案二、现价为:元,
方案三、现价为:元,
,
方案一现价最便宜.
故选:.
先根据题意列出算式:方案一、现价为,方案二、现价为,方案三、现价为,求出结果后比较即可.
本题考查了列代数式,能根据题意列出算式是解此题的关键.
23.【答案】
【解析】解:阴影部分的面积平方厘米;
阴影部分的面积平方厘米;
阴影部分的面积平方厘米;
阴影部分的面积平方厘米;
阴影部分的面积平方厘米.
,
阴影部分面积一样大的图形有个.
故选:.
利用平行四边形面积公式:计算阴影部分的面积;
利用三角形面积公式计算阴影部分的面积;
运用梯形面积公式;计算阴影部分的面积;
阴影部分的面积是一个长是厘米,宽是厘米的长方形的面积,减去个直角三角形的面积.比较即可得出结论.
本题主要考查图形变化类以及图形的面积,关键是根据图形求面积.
24.【答案】
【解析】解:容器的形状上下一样宽,所以水的高度随着时间的变化为均匀的射线,
由于容器的宽度比容器的宽度小,所以上升较快,上升较慢,
故,,
容器的形状下宽,中间逐渐变窄,上层逐渐变宽,所以水的高度上升先慢后快在变慢,图象表现为先缓后陡,最后稍缓,
故,
容器的形状下窄上宽,所以水的高度上升先快后慢,图象表现为先陡后缓,
故.
故选:.
先根据容器的形状,判断水的高度变化情况,进而判断对应的函数图象即可.
本题主要考查函数的图象,根据容器的形状,判断水的高度变化情况,进而得出对应的函数图象是解题关键.
25.【答案】解:
;
.
【解析】先把带分数变成假分数,同时把除法变成乘法,再根据有理数的乘法法则进行计算,最后算减法即可;
先变形,再根据乘法分配律进行变形,最后求出答案即可.
本题考查了有理数的混合运算,能正确运用有理数的运算法则进行计算是解此题的关键,注意运算顺序.
26.【答案】解:,
,
,
,
经检验是原方程的解,
即原方程的解是;
,
,
,
;
,
方程两边都乘,得,
解得:,
检验:当时,,
所以分式方程的解是.
【解析】先根据比例的性质进行计算,再根据等式的性质进行计算即可;
先方程两边都乘,再移项,最后系数化成即可;
方程两边都乘得出,求出方程的解,再进行检验即可.
本题考查了解一元一次方程和解分式方程,能正确根据等式的性质进行变形是解的关键,能把分式方程转化成整式方程是解的关键.
27.【答案】解:人,
人.
答:小军班有人,小丽班有人.
【解析】由题意可知:少的人占小军班人数的,已知一个数的百分之几是多少,求这个数,用除法计算,进一步求得结果即可.
此题考查了百分数的应用,除法应用题的一种基本类型:已知一个数的百分之几是多少,求这个数,用除法计算.
28.【答案】解:由题意得:
万户,
答:该市约有万户家庭.
【解析】先求出公顷落叶阔叶林全年吸收的二氧化碳,再求出每个家庭全年排的二氧化碳,根据户数公顷落叶阔叶林全年吸收的二氧化碳每个家庭全年排的二氧化碳,列出算式进行计算.
本题主要考查了有理数的混合运算,解题关键是理解题意,列出算式.
29.【答案】解:设、两站的距离为千米,
由题意可得:,
解得,
答:、两站的距离是千米.
【解析】根据题意可知:甲走的路程乙走的路程、两站的距离,然后列出方程,再求解即可.
本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程.
第1页,共1页
数学试卷
一、填空题(共28分)
1. ______ : ______ ______
2. 有一个点,它的位置定为,这个点先向上移动格,再向右移动格,则移动后这个点的位置可以表示为______ .
3. 盒子里有同样大小的红、黄、蓝、白四种颜色的球各个,要想摸出的球一定有个是同色的,最少要摸出______ 个球.
4. 阳光小学组织安全意识知识竞赛,共题,评分规则是答对一题得分,答错一题扣分,弃权不扣分也不得分,芳芳小组弃权两题,得了分,他们答对了______ 题
5. 如图,线段长为厘米一只蚂蚁从到沿着四个半圆爬行,蚂蚁的行程是______ 厘米.
6. 两位同学分别对同一个零件按照:和:的比例尺放大,结果图纸上两个零件的长度差厘米,那么这个零件的实际长度是______ 厘米.
7. 在如图中用阴影部分表示公顷.
8. 一个圆柱的底面半径和高相等,那么这个圆柱的底面积和侧面积的比是______ .
9. 旧书店按封底上的标价便宜收购旧书,然后按封底上的标价便宜卖出,旧书店可以获得的利润约是______
10. 五个连续自然数,其中第三个数比第一、第五两数和的少那么第三个数是______ .
11. 三条边长分别是厘米、厘米、厘米的直角三角形,将它的最短边对折与斜边相重合如图那么,图中阴影部分的面积是______ 平方厘米.
12. 在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型如图,如果圆的半径为,扇形半径为,那么: ______ .
13. 根据下面的信息把表格填写完整.
小芳家去年五至八月份的月底电表读数记录表:
月份 五 六 七 八
读数千瓦时 ______ ______
七月份使用空调后,用电量增加了;
七月份用电量是八月份的.
14. 甲、乙两人比赛米的滑雪,乙让甲先滑秒,他们两人滑的路程和时间的关系如图:
在滑雪过程中,______ 滑行的路程与时间成正比关系.
甲滑完全程比乙多用了______ 秒
甲在前秒,平均每秒滑行______ 米;后秒,平均每秒滑行______ 米;滑完全程的平均速度是每秒滑行______ 米除不尽的,结果用分数表示
15. 如果是小于的自然数,那么.______ 判断对错
16. 三个连续自然数的和必定是的倍数.______ 判断对错
17. 王师傅完成一项工作,由于工作效率提高了,故所用的时间节省了.______ 判断对错
18. 的积一定是,,的倍数是大于零的自然数 ______ 判断对错
19. 至少要加上它本身的,才能得到整数.______ 判断对错
二、选择题(本大题共5小题,共10分)
20. 下列哪一幅图的规律和其他图不一样?( )
A. B.
C. D.
21. 把,,,四个数组成比例,其内项的积是( )
A. B. C. D.
22. 超市某种奶粉原价为每千克元,先后两次降价,降价方案有三种:方案一,第一次降价,第二次降价;方案二,第一次降价,第二次降价;方案三,每次都降价,按降价,现价最便宜.( )
A. 方案一 B. 方案二 C. 方案三 D. 不能确定
23. 大正方形的边长是厘米,小正方形的边长是厘米,图形中阴影部分面积一样大的图形有( )
A. 个 B. 个 C. 个 D. 个
24. 如图是水滴进玻璃容器的示意图滴水速度相同,如图表示的是容器中水的高度随滴水时间变化的情况图中刻度、单位都相同下列选项中对应关系正确的是?( )
A. B. C. D.
三、解答题(共82分)
25. 用合理的方法计算:
;
;
26. 求未知数:
;
;
;
27. 小军班有多少人?小丽班有多少人?
小丽:我们班人数比你们班多.
小军:我们班比你们班少人.
28. “低碳生活”从现在做起,从我做起,据测算,公顷落叶阔叶林每年可吸收二氧化碳吨,如果每台空调制冷温度在国家提倡的摄氏度基础上调到摄氏度,相应每年减排二氧化碳千克某市仅此项就大约减排相当于公顷落叶阔叶林全年吸收的二氧化碳,若每个家庭按台空调计算,该市约有多少万户家庭?
29. 甲、乙两车分别从、两站出发相向而行,经过半小时后,甲车行驶了全程的乙车行驶了全程的,这时两车相距千米求、两站的距离.
答案和解析
1.【答案】
【解析】解:;
;
;
.
把小数化成百分数,把小数点向右移动两位,同时在后面加上百分号;把小数化成分数:原来有几位小数,就在的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分;分数化成不同的分数利用分数的基本性质求出即可.
本题考查百分数和分数、小数的互化.抓住之间的关系便可解决问题.
2.【答案】
【解析】解:根据有一个点,它的位置定为,点先向上移动格,行数增加格,列数不变即在,再向右移动格,行数不变,列数增加格,即.
故答案为:.
根据点的平移规律,进而得出答案.
此题主要考查了点的坐标,正确掌握点的平移规律是解题关键.
3.【答案】
【解析】解:根据题意得:
个,
最少要摸出个球.
故答案为:.
从最坏的情况考虑,假设每次摸到的颜色各不相同,则摸次可保证每种颜色的球各个,同理,摸次可保证每种颜色的球各个,再摸个,即可保证摸出的球一定有个是同色.
本题考查了利用抽屉原理解决实际问题,从最坏的情况考虑是解题的关键.
4.【答案】
【解析】解:设他们答对了道,则答错了道,
由题意可得:,
解得,
即他们答对了道题目,
故答案为:.
先设答对题目为道,则可以写出答错题目的道数,根据答对题目得分答错题目得分总得分,可以列出相应的方程,然后求解即可.
本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,列出相应的方程.
5.【答案】
【解析】解:四个半圆弧长的和直径厘米的圆周长的一半,
厘米,
蚂蚁的行程是厘米.
故答案为:.
四个半圆弧长的和直径厘米的圆周长的一半,由圆周长公式即可求解.
本题考查圆的周长,关键是掌握圆周长公式.
6.【答案】
【解析】解:两位同学分别对同一个零件按照:和:的比例尺放大,结果图纸上两个零件的长度差厘米,
这个零件的实际长度是厘米.
故答案为:.
根据比例尺和已知条件得出这个零件的实际长度是,再求出答案即可.
本题考查了比例尺,能熟记比例尺是解此题的关键.
7.【答案】解:如图,阴影部分面积公顷.
【解析】由题意可得每个小长方形的面积为公顷,即可求解.
本题考查了作图基本作图,求出每个小长方形的面积是解题的关键.
8.【答案】:
【解析】解:设圆柱的底面半径和高都是,
则圆柱的底面积为,侧面积为,
这个圆柱的底面积和侧面积的比是::.
故答案为::.
设圆柱的底面半径和高都是,再分别求出圆柱的底面积和侧面积,即可求出答案.
本题主要考查了圆柱的计算,熟练掌握圆柱的底面积和侧面积的计算公式是解题关键.
9.【答案】
【解析】解:
.
答:旧书店可以获得的利润约是.
故答案为:.
根据利润率的意义可知:利润率利润成本;把封底上的标价看作是单位“”,根据利润率的意义进行解答即可.
本题考查了百分数的应用,掌握利润率计算公式”利润率利润成本“是解答本题的关键.
10.【答案】
【解析】解:设中间的一个自然数是,那么第一、五两数和是.
,
,
,
.
答:第三个数是.
故答案为:.
设中间的一个自然数是,因为是一个连续自然数,所以第一个自然数是,第二个自然数是,第四个自然数是,第五个自然数是,把第一、五两数加在一起求和,因为“中间的一个自然数,比第一、五两数和的少,据此等量关系可列方程求解.
解答此题先设出中间的自然数,再表示出其它的自然数,然后根据等量关系列出方程求解.
11.【答案】
【解析】解:如图:
由题意可知:,,,
,
:::,
:::,
平方厘米,
平方厘米,
故答案为:.
通过观察,原直角三角形被分成了三个直角三角形,依据题目条件可以先找出它们的面积比,总面积已知,进而得解.
此题主要考查等底等高的三角形面积相等,解答本题的关键是找准面积的比.
12.【答案】:
【解析】解:因为扇形的弧长等于圆锥底面周长,
所以,
所以
所以 ::;
故答案为::.
根据围成圆锥后圆锥的侧面展开扇形的弧长等于圆锥的底面周长,列出关系式即可得到两个半径之间的关系.
本题考查了圆锥的计算,解答此题的关键是明白:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.
13.【答案】
【解析】解:七月份的用电量为,
所以读数为;
故答案为:;
八月份的用电量为,
所以读数为;
故答案为:.
用六月份的用电量乘以求出七月份的用电量,即可得出答案;
用七月份的用电量除以求出八月份的用电量,即可得出答案.
本题考查了分数混合运算的应用,正确理解题意和准确计算是关键.
14.【答案】乙
【解析】解:由图可知,乙的图象是一条上升的直线,即成正比例关系,
乙滑行的路程与时间成正比关系,
答案为:乙;
甲第秒出发,第秒到终点;乙第秒时出发,第秒到达终点,
即甲全程用时秒,乙全程用时秒,
秒,
甲滑完全程比乙多用了秒,
答案为:;
米秒,
甲前秒速度为:米秒,
米秒,
后秒速度为:米秒,
米秒,
滑完全程的平均速度为:米秒.
答案为:,,.
由图可知,乙的图象是一条上升的直线,即成正比例关系;
甲第秒出发,第秒到终点;乙第秒时出发,第秒到达终点,即甲全程用时秒,乙全程用时秒,即可作答;
用速度路程时间,即可作答.
本题考查一次函数的应用,解题的关键是数形结合.
15.【答案】
【解析】解:是小于的自然数,
,
,故.
故答案为:.
根据是小于的自然数,可得,所以.
本题考查了整数的认识,熟练掌握分数的性质是关键.
16.【答案】对
【解析】解:对.
设三个连续的自然数中的第一个为,第二个为,第二个为.
其和为:,
三个连续的自然数的和,一定是的倍数.
设三个连续的正整数中的第一个为,第二个为,第二个为其和为:,由此即可得出结论.
本题考查的是整式的加减,熟知整式的加减实质上是合并同类项是解答此题的关键.
17.【答案】正确
【解析】解:现在的工作效率是原来的:,
原来的工作效率与现在的工作效率的比是:,
原来的工作时间:现在的工作时间::,
现在的工作时间是原来的,
时间节约了:,
原题说法是正确的.
故答案为:正确.
把原来的工作效率看成单位“”,现在的工作效率是原来的,原来的工作效率与现在的工作效率的比是:,而工作时间与工作效率成反比例,所以原来的工作时间:现在的工作时间:;根据这个比例求出现在的时间是原来的时间的几分之几,进而求出时间节约了百分之几.
本题考查了百分数的应用,解决本题先根据前后两次工作效率之间的比例关系找出它们所用的时间之间的比例关系,再根据求一个数是另一个数的百分之几的方法求解.
18.【答案】
【解析】解:,
是,,的倍数,
的积一定是,,的倍数是大于零的自然数.
故答案为:.
先求出的积,再根据,,的倍数的特征判断即可.
本题考查了倍数和整数的认识,掌握,,的倍数的特征是解答本题的关键.
19.【答案】
【解析】解:
.
所以题干的说法正确.
故答案为:.
把这个分数看作单位“”,比大的最小正整数为,求出两个数之间增加的百分率即可判断是否正确.
本题考查分数的混合运算,掌握分数化整数的方法便可解决问题.
20.【答案】
【解析】解:、;
B、;
C、;
D、.
图与其他图的规律不一样,
故选:.
根据图形中的数字找出规律:右边的数除以左边的数再乘以等于上边的数,从而得出结论.
本题考查图形变化类,关键是根据图形中的数字找出规律.
21.【答案】
【解析】解:,,
,
比例式为::,
两内项的积是.
故选:.
先求出比例式为::,再求出两内项和的积即可.
本题考查了比例的意义,能求出比例式::是解此题的关键.
22.【答案】
【解析】解:方案一、现价为:元,
方案二、现价为:元,
方案三、现价为:元,
,
方案一现价最便宜.
故选:.
先根据题意列出算式:方案一、现价为,方案二、现价为,方案三、现价为,求出结果后比较即可.
本题考查了列代数式,能根据题意列出算式是解此题的关键.
23.【答案】
【解析】解:阴影部分的面积平方厘米;
阴影部分的面积平方厘米;
阴影部分的面积平方厘米;
阴影部分的面积平方厘米;
阴影部分的面积平方厘米.
,
阴影部分面积一样大的图形有个.
故选:.
利用平行四边形面积公式:计算阴影部分的面积;
利用三角形面积公式计算阴影部分的面积;
运用梯形面积公式;计算阴影部分的面积;
阴影部分的面积是一个长是厘米,宽是厘米的长方形的面积,减去个直角三角形的面积.比较即可得出结论.
本题主要考查图形变化类以及图形的面积,关键是根据图形求面积.
24.【答案】
【解析】解:容器的形状上下一样宽,所以水的高度随着时间的变化为均匀的射线,
由于容器的宽度比容器的宽度小,所以上升较快,上升较慢,
故,,
容器的形状下宽,中间逐渐变窄,上层逐渐变宽,所以水的高度上升先慢后快在变慢,图象表现为先缓后陡,最后稍缓,
故,
容器的形状下窄上宽,所以水的高度上升先快后慢,图象表现为先陡后缓,
故.
故选:.
先根据容器的形状,判断水的高度变化情况,进而判断对应的函数图象即可.
本题主要考查函数的图象,根据容器的形状,判断水的高度变化情况,进而得出对应的函数图象是解题关键.
25.【答案】解:
;
.
【解析】先把带分数变成假分数,同时把除法变成乘法,再根据有理数的乘法法则进行计算,最后算减法即可;
先变形,再根据乘法分配律进行变形,最后求出答案即可.
本题考查了有理数的混合运算,能正确运用有理数的运算法则进行计算是解此题的关键,注意运算顺序.
26.【答案】解:,
,
,
,
经检验是原方程的解,
即原方程的解是;
,
,
,
;
,
方程两边都乘,得,
解得:,
检验:当时,,
所以分式方程的解是.
【解析】先根据比例的性质进行计算,再根据等式的性质进行计算即可;
先方程两边都乘,再移项,最后系数化成即可;
方程两边都乘得出,求出方程的解,再进行检验即可.
本题考查了解一元一次方程和解分式方程,能正确根据等式的性质进行变形是解的关键,能把分式方程转化成整式方程是解的关键.
27.【答案】解:人,
人.
答:小军班有人,小丽班有人.
【解析】由题意可知:少的人占小军班人数的,已知一个数的百分之几是多少,求这个数,用除法计算,进一步求得结果即可.
此题考查了百分数的应用,除法应用题的一种基本类型:已知一个数的百分之几是多少,求这个数,用除法计算.
28.【答案】解:由题意得:
万户,
答:该市约有万户家庭.
【解析】先求出公顷落叶阔叶林全年吸收的二氧化碳,再求出每个家庭全年排的二氧化碳,根据户数公顷落叶阔叶林全年吸收的二氧化碳每个家庭全年排的二氧化碳,列出算式进行计算.
本题主要考查了有理数的混合运算,解题关键是理解题意,列出算式.
29.【答案】解:设、两站的距离为千米,
由题意可得:,
解得,
答:、两站的距离是千米.
【解析】根据题意可知:甲走的路程乙走的路程、两站的距离,然后列出方程,再求解即可.
本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程.
第1页,共1页
同课章节目录
