人教版七年级数学上册4.3.2角的比较与运算 导学案(知识清单+典型例题+巩固提升)(含解析)
文档属性
| 名称 | 人教版七年级数学上册4.3.2角的比较与运算 导学案(知识清单+典型例题+巩固提升)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级数学上册 4.3.2 角的比较与运算 导学案
【知识清单】
角的单位:度,分,秒 ①1°的60分之一为1分,记作1′,即1°=60′
②1′的60分之一为1秒,记作1″,即1′=60″
角的大小比较:⑴度量法;⑵叠合法。
角平分线:从一个角的顶点引出一条射线,把这个角分成两个等角,这条射线叫角平分线。
【典型例题】
考点1:角的单位与角度制
例1.下列关系式正确的是( )
A. B. C. D.
【答案】D
【分析】先根据角的换算得到,即可求解.
【详解】解:∵,
∴,
故选:D.
【点睛】本题考查角的大小比较,掌握角度的换算是解题的关键.
考点2:角的度数与比较
例2.下列说法正确的个数是( )
①木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;②若,则点C是的中点;③若,,,则有.
A.1个 B.2个 C.3个 D.0个
【答案】A
【分析】①根据直线的性质判断即可;②根据中点的概念判断即可;③先换算单位,再进行比较.
【详解】①木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是∶两点确定一条直线,故说法错误;
②若,则点C不一定是的中点,也可能在的延长线上或三点不共线,故说法错误;
③若,,,则有,故说法正确;
故选∶A.
【点睛】本题考查的是角的大小比较以及线段和直线的性质,关键是明白.
考点3:角的四则运算
例3.( )
A. B. C. D.
【答案】A
【分析】根据度分秒的加法法则计算即可.
【详解】,
故选:A.
【点睛】本题考查度分秒的加减运算,熟记运算法则是解题的关键.
考点4:角平分线及计算
例4.如图,,平分,若,则( )
A. B. C. D.
【答案】A
【分析】根据角平分线的定义可得,即,根据等角的余角相等,可得,则,根据已知条件,即可求解.
【详解】解:∵平分,
∴,
∴
∵,
∴
∴,
∴,
∵
∴
∴,
故选:A.
【点睛】本题考查了角平分线的定义,等角的余角相等,求一个角的余角,数形结合得出是解题的关键.
【巩固提升】
1.若,则用度、分、秒表示为( )
A. B. C. D.
2.在下列说法中,正确的是( )
A.比较角的大小就是比较角的度数大小
B.从角的顶点出发的一条射线把这个角分成两个角,这条射线叫做这个角的平分线
C.若,则OC是∠AOB的平分线
D.用一个放大镜能够把一个图形放大,也能够把一个角的度数放大
3.如图1,图2所示,把一副三角板先后放在上,则的度数可能( )
A. B. C. D.
4.我们用一副三角板能画出的特殊角中,最小角度是( )
A. B. C. D.
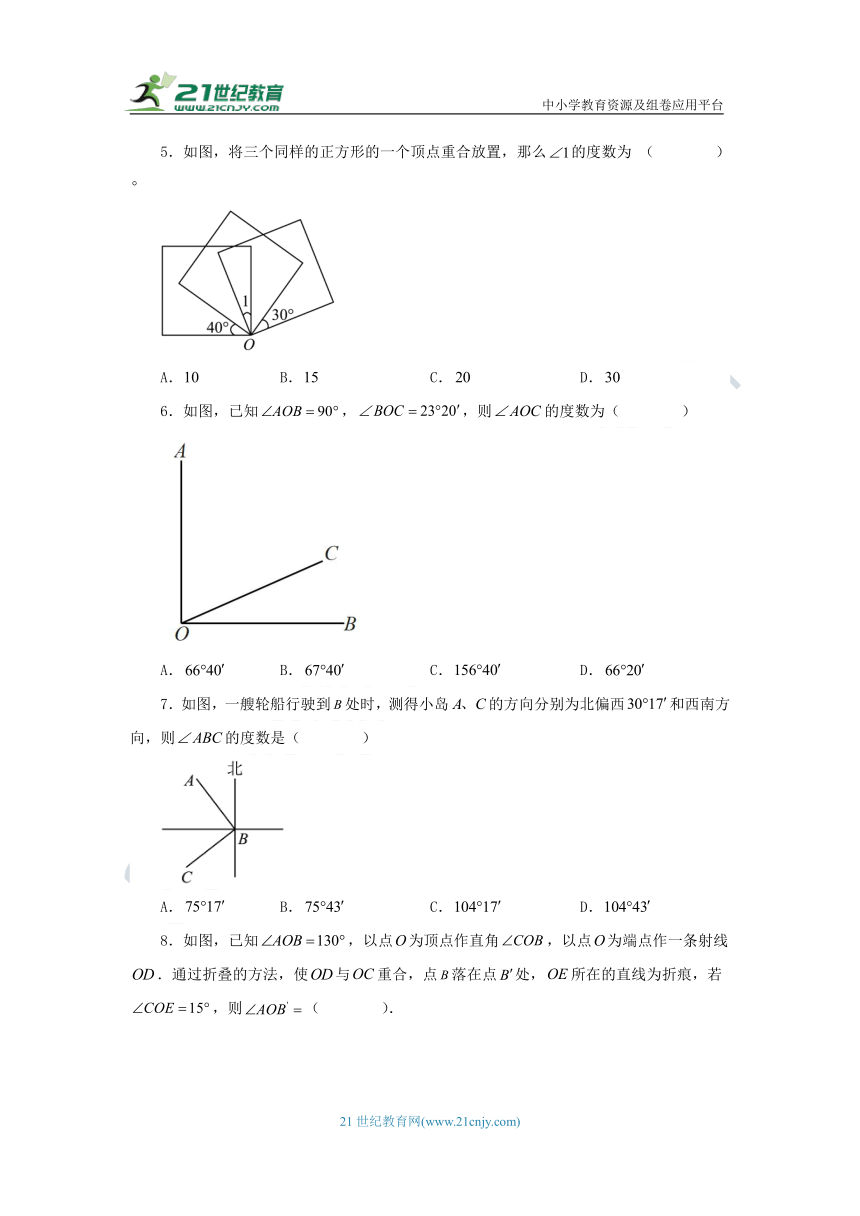
5.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为 ( )
A. B. C. D.
6.如图,已知,,则的度数为( )
A. B. C. D.
7.如图,一艘轮船行驶到处时,测得小岛的方向分别为北偏西和西南方向,则的度数是( )
A. B. C. D.
8.如图,已知,以点为顶点作直角,以点为端点作一条射线.通过折叠的方法,使与重合,点落在点处,所在的直线为折痕,若,则( ).
A. B. C. D.
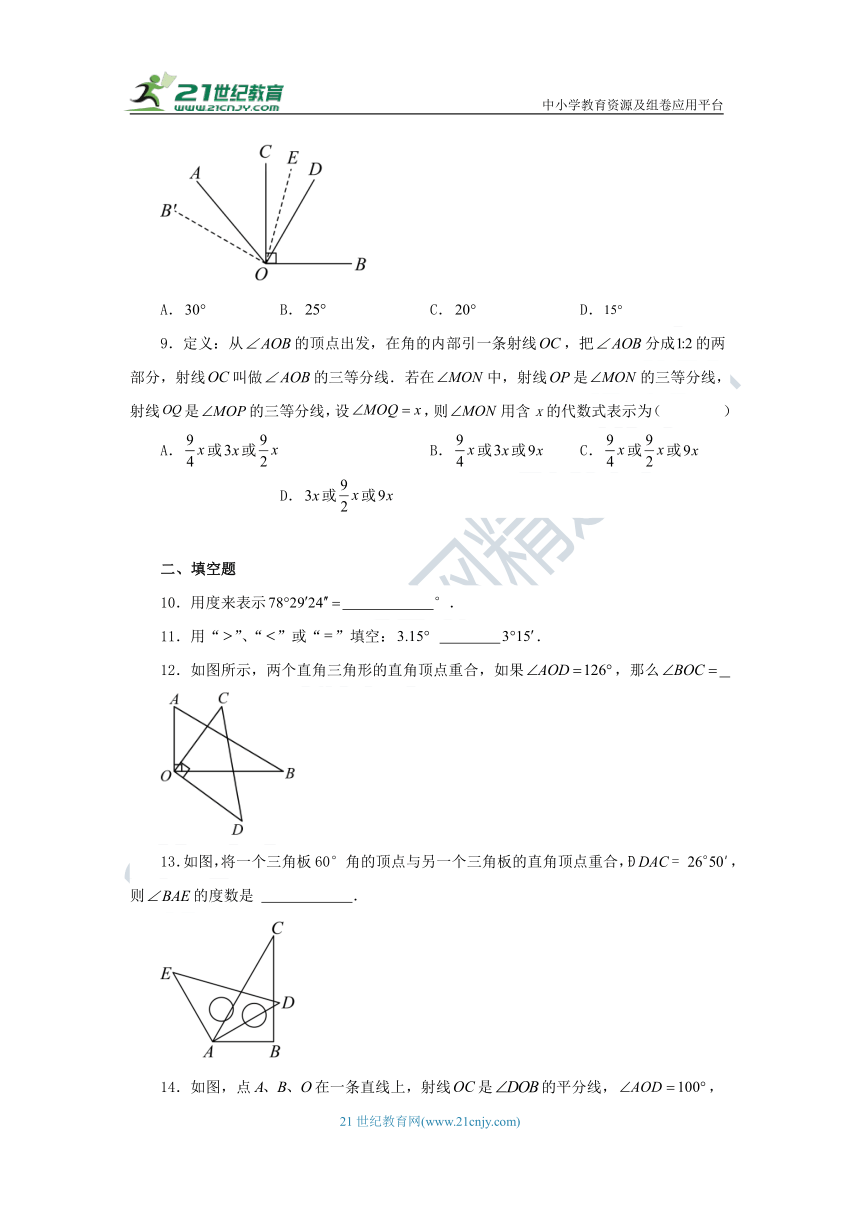
9.定义:从的顶点出发,在角的内部引一条射线,把分成的两部分,射线叫做的三等分线.若在中,射线是的三等分线,射线是的三等分线,设,则用含x的代数式表示为( )
A.或或 B.或或 C.或或 D.或或
二、填空题
10.用度来表示 °.
11.用“”、“”或“”填空: .
12.如图所示,两个直角三角形的直角顶点重合,如果,那么
13.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,,则的度数是 .
14.如图,点在一条直线上,射线是的平分线,, .
三、解答题
15.尺规作图:如图,已知线段a.
(1)作线段;
(2)用圆规在线段的延长线上截取,然后作线段(点C在直线外);
(3)连接,,并用量角器测量约为________°(精确到度).
注意:以上作图不写作法,保留作图痕迹.
16.请根据图回答下列问题.
(1)表示成,表示成,表示成,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?请列举出来.
17.已知O为直线上一点,作射线、、,且平分.
(1)如图1,当、、均在上方时,若,,则______.
(2)如图2,当、在上方,在的下方时,若,,求的度数.
(3)在(2)的条件下,作射线,若,请画出图形,并求的度数.
18.计算下列各题:
(1);
(2);
(3)
19.如图,已知,,求的度数.
20.如图,是平角,是射线,平分,平分,.求的度数.
21.如图,是的平分线,是的平分线,且.
(1)求的度数;
(2)若,直接写出的度数.
参考答案
1.B
【分析】利用度分秒之间的换算关系进行计算即可求解;
【详解】
故选:B
【点睛】本题考查了度分秒的换算,掌握 , 是关键
2.A
【分析】根据角的大小比较方法与角平分线的定义对各小题进行逐一分析即可.
【详解】解:A. 比较角的大小就是比较角的度数大小,故本选项正确;
B. 从角的顶点出发的一条射线把这个角分成相等的两个角,这条射线叫做这个角的平分线,故本选项错误;
C. 若,且在内部,则是的平分线,故本选项错误;
D.放大镜能够把一个图形放大,不能够把一个角的度数放大,故本选项错误.
故选:A.
【点睛】本题考查的是角的大小比较,角平分线的定义,熟知角比较大小的法则是解答此题的关键.
3.C
【分析】根据三角板的特点可得,结合选项即得答案.
【详解】解:由图1可得,由图2可得,
∴,
故选:C.
【点睛】本题考查了三角板的特点,正确得出是解题的关键.
4.D
【分析】根据三角板的角度,计算和差可得结果.
【详解】解:一副三角板共两块,一块是三个内角分别为、、;另一块是三个内角分别为、、,
用一块三角板的角减去另一块三角板的角,求出的就是最小角度,即.
故选:D.
【点睛】本题主要考查角的计算,熟悉两块三角板度数是解题的关键.
5.C
【分析】根据,利用正方形的角都是直角,即可求得和的度数从而求解.
【详解】解:如图,
根据题意得:,,
又∵,
∴.
故选:C.
【点睛】本题主要考查了角度的计算,正确理解这一关系是解决本题的关键.
6.A
【分析】用减去即可.
【详解】解:,
故选A.
【点睛】本题考查了角的计算,解题的关键是根据图形得出角的和差关系.
7.D
【分析】根据题意可得,再根据平角的定义求解即可.
【详解】解:根据题意可得:,
∴;
故选:D.
【点睛】本题考查了方位角和角的和差计算,正确得出是解题的关键.
8.C
【分析】利用角平分线的定义求出即可解决问题.
【详解】解:平分,
,
,
,
,
,
,
故选:C.
【点睛】本题考查角的和差定义,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.C
【分析】分四种情况,分别计算,即可求解.
【详解】解:如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
综上,为或或,
故选:C.
【点睛】本题考查了角的有关计算,画出图形,采用分类讨论的思想是解决本题的关键.
10.
【分析】先将化成,再将化成“度”即可.
【详解】解:,
,
,
.
故答案为:.
【点睛】本题考查了度、分、秒之间的换算的应用,能正确进行度、分、秒之间的换算是解此题的关键,注意:,.
11.
【分析】根据角度换算,将表示角度的两种形式化统一再比较大小即可得到答案.
【详解】解:,
,
,
,
故答案为:.
【点睛】本题考查角度比较大小,熟练掌握角度换算是解决问题的关键.
12./度
【分析】根据题意得到,再计算,然后根据进行计算即可.
【详解】解:,
而,
,
.
故答案为:.
【点睛】本题考查了角的计算,关键是熟记:直角,平角.
13.
【分析】根据,可计算出的度数,再由,即可得出答案.
【详解】解:∵,,
∴,
∵,
∴.
故答案为:.
【点睛】本题考查角度的计算,理解角的度量单位及计算法则是解题的关键.
14.
【分析】根据平角的计算可得的度数,根据角平分线的性质可求出的度数,由此即可求解.
【详解】解:∵点在一条直线上,
∴,且,
∴,
∵是的平分线,
∴,
故答案为:.
【点睛】本题主要考查角平分线的性质,掌握平角的计算,角平分线的性质是解题的关键.
15.(1)见详解
(2)见详解
(3)
【分析】(1)根据尺规作图即可;
(2)根据尺规作图即可;
(3)直接量角器测量即可.
【详解】(1)解:如图,
线段即为所求.
(2)线段,
,即为所求.
(3)用量角器测量约为,
故答案为:.
【点睛】本题考查了基本的线段作图,解决本题的关键是利用好尺规进行作图.
16.(1)表示方法不对,表示成,表示成,表示成
(2)
(3)11个,列举见解析
【分析】(1)(2)根据角的表示方法进行求解即可;
(3)只需要表示出小于180度的角即可.
【详解】(1)解:表示成,表示成,表示成,这样的表示方法不对,正确的表示方法为 表示成,表示成,表示成
(2)解:图中可以用一个字母表示的角为
(3)解:图中小于平角的角有∴一共有11个角小于平角.
【点睛】本题主要考查了角的表示方法,熟知角的表示方法是解题的关键.
17.(1)
(2)
(3)或
【分析】(1)先求解,结合角平分线可得,再利用角的和差关系可得答案;
(2)先求解,结合角平分线的含义可得,再利用角的和差关系可得答案;
(3)如图一:当在的上方时,先求解,再利用角的和差关系可得答案;如图二:当在的下方时,先求解,结合,再利用角的和差关系可得答案.
【详解】(1)解:∵,
∴,
∵平分,
∴,
∵,
∴;
(2)∵,,
∴,
又平分,
∴,
∴,
,
;
(3)如图一:当在的上方时,
∵,,
∴
∴
如图二:当在的下方时,
∵ ,,
∴
又∵
∴
.
【点睛】本题考查的是角的和差运算,角平分线的定义,熟练的利用角的和差关系进行计算是解本题的关键.
18.(1)
(2)
(3)
【分析】(1)从左往右依次计算;
(2)去括号,合并同类项即可;
(3)将度与度相加,分与分相加,再化简.
【详解】(1)解:原式
;
(2)原式
;
(3)原式
【点睛】本题考查了有理数的加减运算,整式的加减运算,角的运算,解题的关键是掌握相应的运算法则.
19.
【分析】根据,则,推出;根据,求出,根据,即可.
【详解】∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
【点睛】本题考查角的度量,解题的关键是掌握各角之间的等量关系,进行角的计算.
20.
【分析】根据角平分线的定义和平角是求解即可.
【详解】如图,∵平分,,
∴.
∵是平角,
∴.
又∵平分,
∴.
【点睛】本题考查角平分线的定义、平角定义,熟练掌握角平分线的定义是解答的关键.
21.(1)
(2)
【分析】(1)利用角平分线的的定义依次求出、即可;
(2)利用角平分线的的定义依次用表示、即可;
【详解】(1)解:,是的平分线,
,
是的平分线,
.
(2)解:;
,是的平分线,
,
是的平分线,
.
【点睛】本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.
21世纪教育网(www.21cnjy.com)
人教版七年级数学上册 4.3.2 角的比较与运算 导学案
【知识清单】
角的单位:度,分,秒 ①1°的60分之一为1分,记作1′,即1°=60′
②1′的60分之一为1秒,记作1″,即1′=60″
角的大小比较:⑴度量法;⑵叠合法。
角平分线:从一个角的顶点引出一条射线,把这个角分成两个等角,这条射线叫角平分线。
【典型例题】
考点1:角的单位与角度制
例1.下列关系式正确的是( )
A. B. C. D.
【答案】D
【分析】先根据角的换算得到,即可求解.
【详解】解:∵,
∴,
故选:D.
【点睛】本题考查角的大小比较,掌握角度的换算是解题的关键.
考点2:角的度数与比较
例2.下列说法正确的个数是( )
①木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;②若,则点C是的中点;③若,,,则有.
A.1个 B.2个 C.3个 D.0个
【答案】A
【分析】①根据直线的性质判断即可;②根据中点的概念判断即可;③先换算单位,再进行比较.
【详解】①木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是∶两点确定一条直线,故说法错误;
②若,则点C不一定是的中点,也可能在的延长线上或三点不共线,故说法错误;
③若,,,则有,故说法正确;
故选∶A.
【点睛】本题考查的是角的大小比较以及线段和直线的性质,关键是明白.
考点3:角的四则运算
例3.( )
A. B. C. D.
【答案】A
【分析】根据度分秒的加法法则计算即可.
【详解】,
故选:A.
【点睛】本题考查度分秒的加减运算,熟记运算法则是解题的关键.
考点4:角平分线及计算
例4.如图,,平分,若,则( )
A. B. C. D.
【答案】A
【分析】根据角平分线的定义可得,即,根据等角的余角相等,可得,则,根据已知条件,即可求解.
【详解】解:∵平分,
∴,
∴
∵,
∴
∴,
∴,
∵
∴
∴,
故选:A.
【点睛】本题考查了角平分线的定义,等角的余角相等,求一个角的余角,数形结合得出是解题的关键.
【巩固提升】
1.若,则用度、分、秒表示为( )
A. B. C. D.
2.在下列说法中,正确的是( )
A.比较角的大小就是比较角的度数大小
B.从角的顶点出发的一条射线把这个角分成两个角,这条射线叫做这个角的平分线
C.若,则OC是∠AOB的平分线
D.用一个放大镜能够把一个图形放大,也能够把一个角的度数放大
3.如图1,图2所示,把一副三角板先后放在上,则的度数可能( )
A. B. C. D.
4.我们用一副三角板能画出的特殊角中,最小角度是( )
A. B. C. D.
5.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为 ( )
A. B. C. D.
6.如图,已知,,则的度数为( )
A. B. C. D.
7.如图,一艘轮船行驶到处时,测得小岛的方向分别为北偏西和西南方向,则的度数是( )
A. B. C. D.
8.如图,已知,以点为顶点作直角,以点为端点作一条射线.通过折叠的方法,使与重合,点落在点处,所在的直线为折痕,若,则( ).
A. B. C. D.
9.定义:从的顶点出发,在角的内部引一条射线,把分成的两部分,射线叫做的三等分线.若在中,射线是的三等分线,射线是的三等分线,设,则用含x的代数式表示为( )
A.或或 B.或或 C.或或 D.或或
二、填空题
10.用度来表示 °.
11.用“”、“”或“”填空: .
12.如图所示,两个直角三角形的直角顶点重合,如果,那么
13.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,,则的度数是 .
14.如图,点在一条直线上,射线是的平分线,, .
三、解答题
15.尺规作图:如图,已知线段a.
(1)作线段;
(2)用圆规在线段的延长线上截取,然后作线段(点C在直线外);
(3)连接,,并用量角器测量约为________°(精确到度).
注意:以上作图不写作法,保留作图痕迹.
16.请根据图回答下列问题.
(1)表示成,表示成,表示成,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?请列举出来.
17.已知O为直线上一点,作射线、、,且平分.
(1)如图1,当、、均在上方时,若,,则______.
(2)如图2,当、在上方,在的下方时,若,,求的度数.
(3)在(2)的条件下,作射线,若,请画出图形,并求的度数.
18.计算下列各题:
(1);
(2);
(3)
19.如图,已知,,求的度数.
20.如图,是平角,是射线,平分,平分,.求的度数.
21.如图,是的平分线,是的平分线,且.
(1)求的度数;
(2)若,直接写出的度数.
参考答案
1.B
【分析】利用度分秒之间的换算关系进行计算即可求解;
【详解】
故选:B
【点睛】本题考查了度分秒的换算,掌握 , 是关键
2.A
【分析】根据角的大小比较方法与角平分线的定义对各小题进行逐一分析即可.
【详解】解:A. 比较角的大小就是比较角的度数大小,故本选项正确;
B. 从角的顶点出发的一条射线把这个角分成相等的两个角,这条射线叫做这个角的平分线,故本选项错误;
C. 若,且在内部,则是的平分线,故本选项错误;
D.放大镜能够把一个图形放大,不能够把一个角的度数放大,故本选项错误.
故选:A.
【点睛】本题考查的是角的大小比较,角平分线的定义,熟知角比较大小的法则是解答此题的关键.
3.C
【分析】根据三角板的特点可得,结合选项即得答案.
【详解】解:由图1可得,由图2可得,
∴,
故选:C.
【点睛】本题考查了三角板的特点,正确得出是解题的关键.
4.D
【分析】根据三角板的角度,计算和差可得结果.
【详解】解:一副三角板共两块,一块是三个内角分别为、、;另一块是三个内角分别为、、,
用一块三角板的角减去另一块三角板的角,求出的就是最小角度,即.
故选:D.
【点睛】本题主要考查角的计算,熟悉两块三角板度数是解题的关键.
5.C
【分析】根据,利用正方形的角都是直角,即可求得和的度数从而求解.
【详解】解:如图,
根据题意得:,,
又∵,
∴.
故选:C.
【点睛】本题主要考查了角度的计算,正确理解这一关系是解决本题的关键.
6.A
【分析】用减去即可.
【详解】解:,
故选A.
【点睛】本题考查了角的计算,解题的关键是根据图形得出角的和差关系.
7.D
【分析】根据题意可得,再根据平角的定义求解即可.
【详解】解:根据题意可得:,
∴;
故选:D.
【点睛】本题考查了方位角和角的和差计算,正确得出是解题的关键.
8.C
【分析】利用角平分线的定义求出即可解决问题.
【详解】解:平分,
,
,
,
,
,
,
故选:C.
【点睛】本题考查角的和差定义,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.C
【分析】分四种情况,分别计算,即可求解.
【详解】解:如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
综上,为或或,
故选:C.
【点睛】本题考查了角的有关计算,画出图形,采用分类讨论的思想是解决本题的关键.
10.
【分析】先将化成,再将化成“度”即可.
【详解】解:,
,
,
.
故答案为:.
【点睛】本题考查了度、分、秒之间的换算的应用,能正确进行度、分、秒之间的换算是解此题的关键,注意:,.
11.
【分析】根据角度换算,将表示角度的两种形式化统一再比较大小即可得到答案.
【详解】解:,
,
,
,
故答案为:.
【点睛】本题考查角度比较大小,熟练掌握角度换算是解决问题的关键.
12./度
【分析】根据题意得到,再计算,然后根据进行计算即可.
【详解】解:,
而,
,
.
故答案为:.
【点睛】本题考查了角的计算,关键是熟记:直角,平角.
13.
【分析】根据,可计算出的度数,再由,即可得出答案.
【详解】解:∵,,
∴,
∵,
∴.
故答案为:.
【点睛】本题考查角度的计算,理解角的度量单位及计算法则是解题的关键.
14.
【分析】根据平角的计算可得的度数,根据角平分线的性质可求出的度数,由此即可求解.
【详解】解:∵点在一条直线上,
∴,且,
∴,
∵是的平分线,
∴,
故答案为:.
【点睛】本题主要考查角平分线的性质,掌握平角的计算,角平分线的性质是解题的关键.
15.(1)见详解
(2)见详解
(3)
【分析】(1)根据尺规作图即可;
(2)根据尺规作图即可;
(3)直接量角器测量即可.
【详解】(1)解:如图,
线段即为所求.
(2)线段,
,即为所求.
(3)用量角器测量约为,
故答案为:.
【点睛】本题考查了基本的线段作图,解决本题的关键是利用好尺规进行作图.
16.(1)表示方法不对,表示成,表示成,表示成
(2)
(3)11个,列举见解析
【分析】(1)(2)根据角的表示方法进行求解即可;
(3)只需要表示出小于180度的角即可.
【详解】(1)解:表示成,表示成,表示成,这样的表示方法不对,正确的表示方法为 表示成,表示成,表示成
(2)解:图中可以用一个字母表示的角为
(3)解:图中小于平角的角有∴一共有11个角小于平角.
【点睛】本题主要考查了角的表示方法,熟知角的表示方法是解题的关键.
17.(1)
(2)
(3)或
【分析】(1)先求解,结合角平分线可得,再利用角的和差关系可得答案;
(2)先求解,结合角平分线的含义可得,再利用角的和差关系可得答案;
(3)如图一:当在的上方时,先求解,再利用角的和差关系可得答案;如图二:当在的下方时,先求解,结合,再利用角的和差关系可得答案.
【详解】(1)解:∵,
∴,
∵平分,
∴,
∵,
∴;
(2)∵,,
∴,
又平分,
∴,
∴,
,
;
(3)如图一:当在的上方时,
∵,,
∴
∴
如图二:当在的下方时,
∵ ,,
∴
又∵
∴
.
【点睛】本题考查的是角的和差运算,角平分线的定义,熟练的利用角的和差关系进行计算是解本题的关键.
18.(1)
(2)
(3)
【分析】(1)从左往右依次计算;
(2)去括号,合并同类项即可;
(3)将度与度相加,分与分相加,再化简.
【详解】(1)解:原式
;
(2)原式
;
(3)原式
【点睛】本题考查了有理数的加减运算,整式的加减运算,角的运算,解题的关键是掌握相应的运算法则.
19.
【分析】根据,则,推出;根据,求出,根据,即可.
【详解】∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
【点睛】本题考查角的度量,解题的关键是掌握各角之间的等量关系,进行角的计算.
20.
【分析】根据角平分线的定义和平角是求解即可.
【详解】如图,∵平分,,
∴.
∵是平角,
∴.
又∵平分,
∴.
【点睛】本题考查角平分线的定义、平角定义,熟练掌握角平分线的定义是解答的关键.
21.(1)
(2)
【分析】(1)利用角平分线的的定义依次求出、即可;
(2)利用角平分线的的定义依次用表示、即可;
【详解】(1)解:,是的平分线,
,
是的平分线,
.
(2)解:;
,是的平分线,
,
是的平分线,
.
【点睛】本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.
21世纪教育网(www.21cnjy.com)
