21.3一元二次方程的应用(二) 随堂过关 (含答案)
文档属性
| 名称 | 21.3一元二次方程的应用(二) 随堂过关 (含答案) | 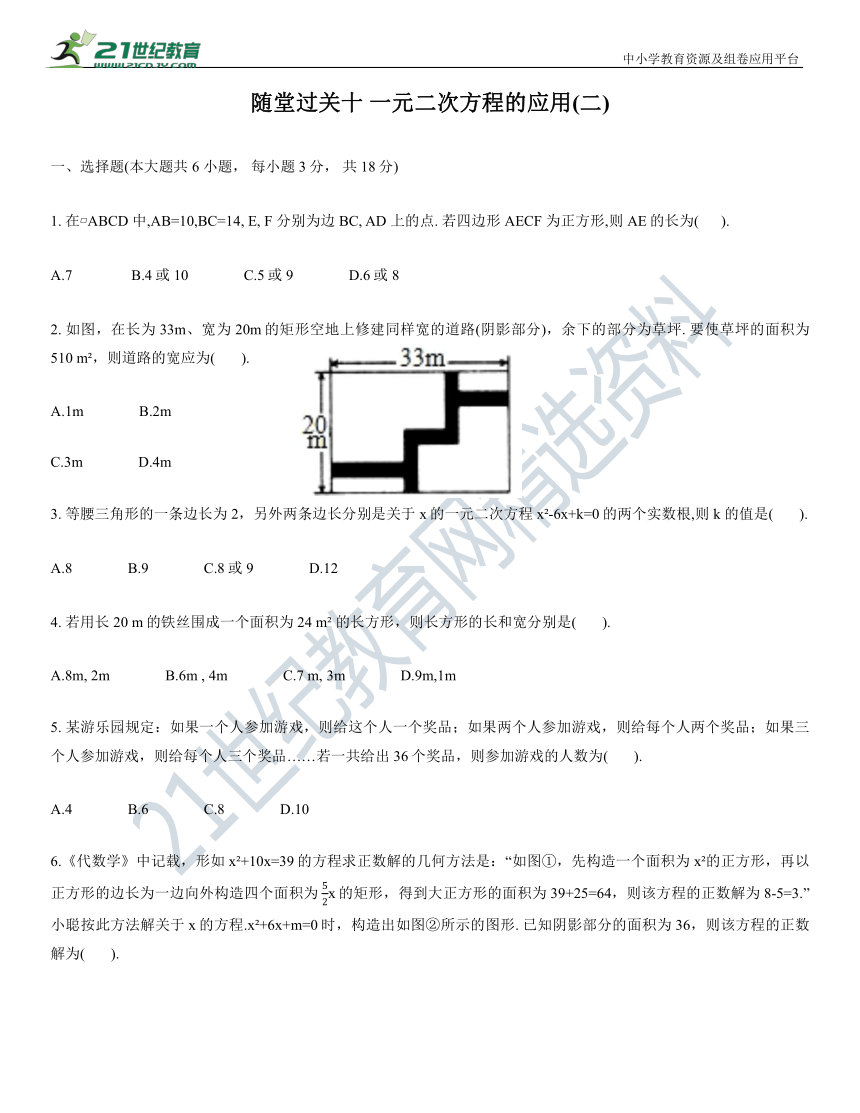 | |
| 格式 | docx | ||
| 文件大小 | 515.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 11:20:13 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
随堂过关十 一元二次方程的应用(二)
一、选择题(本大题共 6 小题, 每小题3分, 共 18分)
1. 在 ABCD 中,AB=10,BC=14, E, F 分别为边 BC, AD 上的点. 若四边形AECF 为正方形,则AE的长为( ).
A.7 B.4或10 C.5或9 D.6或8
2. 如图,在长为33m、宽为20m的矩形空地上修建同样宽的道路(阴影部分),余下的部分为草坪. 要使草坪的面积为510 m ,则道路的宽应为( ).
A.1m B.2m
C.3m D.4m
3. 等腰三角形的一条边长为2,另外两条边长分别是关于x的一元二次方程x -6x+k=0的两个实数根,则k 的值是( ).
A.8 B.9 C.8或9 D.12
4. 若用长20 m的铁丝围成一个面积为24 m 的长方形,则长方形的长和宽分别是( ).
A.8m, 2m B.6m , 4m C.7 m, 3m D.9m,1m
5. 某游乐园规定:如果一个人参加游戏,则给这个人一个奖品;如果两个人参加游戏,则给每个人两个奖品;如果三个人参加游戏,则给每个人三个奖品……若一共给出36个奖品,则参加游戏的人数为( ).
A.4 B.6 C.8 D.10
6.《代数学》中记载,形如x +10x=39的方程求正数解的几何方法是:“如图①,先构造一个面积为x 的正方形,再以正方形的边长为一边向外构造四个面积为 x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3.”小聪按此方法解关于x的方程.x +6x+m=0时,构造出如图②所示的图形. 已知阴影部分的面积为36,则该方程的正数解为( ).
A. x=6
二、填空题(本大题共4 小题, 每小题3分, 共12分)
7. 已知一块长方形铁片的面积为 150 cm ,它的长比宽多5cm,则长方形铁片的长是_______cm,宽是_______cm.
8. 若直角三角形的两条直角边长的差为7,斜边长为13,则它的面积为_______.
9. 从一块正方形铁片上截去一个宽为5cm 的长方形,剩下的面积是24 cm ,则原来这块铁片的面积是_______cm .
10. 东西街道和南北街道交于点 O(假设街道足够长), 甲、乙两人同时从点O出发,甲沿东西街道由西向东走,速度为4m/s;乙沿南北街道由南向北走,速度为3m/s,多少秒后两人相距50m 设两人出发ts后相距50m,由题意可列方程为_______.
三、解答题(本大题共2小题,每小题 10分,共20分. 解答时应写出必要的文字说明、证明过程或演算步骤)
11. 要为一幅长29 cm、宽22cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,则镜框边的宽度应是多少 (结果精确到0.1cm)
12. 已知 ABCD的两边AB,AD的长是关于x的一元二次方程. 的两个实数根.
(1)当m为何值时,四边形ABCD 是菱形 求出这时菱形的边长.
(2)若AB 的长为2,则 ABCD 的周长是多少
随堂过关十 一元二次方程的应用(二)
1. D 2. C 3. B 4. B 5. B 6. B
7.15 10 8.30 9.64 10.(4t) +(3t) =50
11. 设镜框边的宽度为x cm,由题意,得(
整理,得8x +204x-319=0,
解得
∴x ≈1.5,x ≈-27.0(不合题意,舍去),
故镜框边的宽度约为 1.5cm .
12.(1)∵四边形ABCD 是菱形, ∴AB=AD.
又
∴当(m-1) =0,即m=1时,四边形ABCD是菱形.
把m=1代入 得 解得
∴菱形ABCD的边长是 .
(2)把AB=2代入 得 解得
把 代入 得
解得
∵四边形ABCD是平行四边形,
∴□ABCD 的周长是
随堂过关十 一元二次方程的应用(二)
一、选择题(本大题共 6 小题, 每小题3分, 共 18分)
1. 在 ABCD 中,AB=10,BC=14, E, F 分别为边 BC, AD 上的点. 若四边形AECF 为正方形,则AE的长为( ).
A.7 B.4或10 C.5或9 D.6或8
2. 如图,在长为33m、宽为20m的矩形空地上修建同样宽的道路(阴影部分),余下的部分为草坪. 要使草坪的面积为510 m ,则道路的宽应为( ).
A.1m B.2m
C.3m D.4m
3. 等腰三角形的一条边长为2,另外两条边长分别是关于x的一元二次方程x -6x+k=0的两个实数根,则k 的值是( ).
A.8 B.9 C.8或9 D.12
4. 若用长20 m的铁丝围成一个面积为24 m 的长方形,则长方形的长和宽分别是( ).
A.8m, 2m B.6m , 4m C.7 m, 3m D.9m,1m
5. 某游乐园规定:如果一个人参加游戏,则给这个人一个奖品;如果两个人参加游戏,则给每个人两个奖品;如果三个人参加游戏,则给每个人三个奖品……若一共给出36个奖品,则参加游戏的人数为( ).
A.4 B.6 C.8 D.10
6.《代数学》中记载,形如x +10x=39的方程求正数解的几何方法是:“如图①,先构造一个面积为x 的正方形,再以正方形的边长为一边向外构造四个面积为 x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3.”小聪按此方法解关于x的方程.x +6x+m=0时,构造出如图②所示的图形. 已知阴影部分的面积为36,则该方程的正数解为( ).
A. x=6
二、填空题(本大题共4 小题, 每小题3分, 共12分)
7. 已知一块长方形铁片的面积为 150 cm ,它的长比宽多5cm,则长方形铁片的长是_______cm,宽是_______cm.
8. 若直角三角形的两条直角边长的差为7,斜边长为13,则它的面积为_______.
9. 从一块正方形铁片上截去一个宽为5cm 的长方形,剩下的面积是24 cm ,则原来这块铁片的面积是_______cm .
10. 东西街道和南北街道交于点 O(假设街道足够长), 甲、乙两人同时从点O出发,甲沿东西街道由西向东走,速度为4m/s;乙沿南北街道由南向北走,速度为3m/s,多少秒后两人相距50m 设两人出发ts后相距50m,由题意可列方程为_______.
三、解答题(本大题共2小题,每小题 10分,共20分. 解答时应写出必要的文字说明、证明过程或演算步骤)
11. 要为一幅长29 cm、宽22cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,则镜框边的宽度应是多少 (结果精确到0.1cm)
12. 已知 ABCD的两边AB,AD的长是关于x的一元二次方程. 的两个实数根.
(1)当m为何值时,四边形ABCD 是菱形 求出这时菱形的边长.
(2)若AB 的长为2,则 ABCD 的周长是多少
随堂过关十 一元二次方程的应用(二)
1. D 2. C 3. B 4. B 5. B 6. B
7.15 10 8.30 9.64 10.(4t) +(3t) =50
11. 设镜框边的宽度为x cm,由题意,得(
整理,得8x +204x-319=0,
解得
∴x ≈1.5,x ≈-27.0(不合题意,舍去),
故镜框边的宽度约为 1.5cm .
12.(1)∵四边形ABCD 是菱形, ∴AB=AD.
又
∴当(m-1) =0,即m=1时,四边形ABCD是菱形.
把m=1代入 得 解得
∴菱形ABCD的边长是 .
(2)把AB=2代入 得 解得
把 代入 得
解得
∵四边形ABCD是平行四边形,
∴□ABCD 的周长是
同课章节目录
