湘教版九年级上册 3《图形的相似》 单元练习(含答案)
文档属性
| 名称 | 湘教版九年级上册 3《图形的相似》 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 16:47:43 | ||
图片预览




文档简介
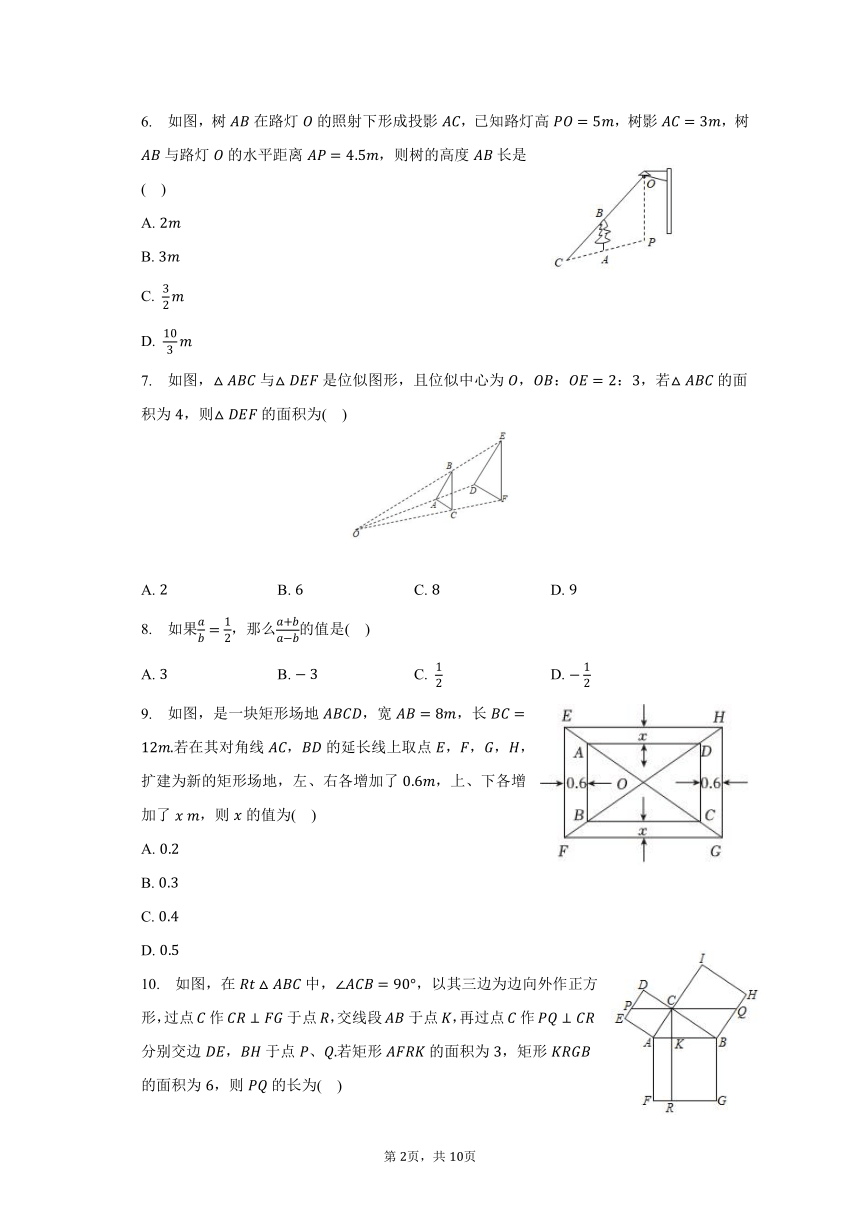
湘教版九年级上册《图形的相似》 单元练习
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1. 如果::,::那么:( )
A. : B. : C. : D. :
2. 下面的四个数中能组成比例的是( )
A. 、、和 B. 、、和
C. 、、和 D. 、、和
3. 如图,在中,,,,,则的长为
( )
A. B. C. D.
4. 下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A. B. C. D.
5. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,∽,则的度数为( )
A. B. C. D.
6. 如图,树在路灯的照射下形成投影,已知路灯高,树影,树与路灯的水平距离,则树的高度长是( )
A.
B.
C.
D.
7. 如图,与是位似图形,且位似中心为,::,若的面积为,则的面积为( )
A. B. C. D.
8. 如果,那么的值是( )
A. B. C. D.
9. 如图,是一块矩形场地,宽,长若在其对角线,的延长线上取点,,,,扩建为新的矩形场地,左、右各增加了,上、下各增加了,则的值为( )
A.
B.
C.
D.
10. 如图,在中,,以其三边为边向外作正方形,过点作于点,交线段于点,再过点作分别交边,于点、若矩形的面积为,矩形的面积为,则的长为( )
A.
B.
C.
D.
二、填空题(本大题共8小题)
11. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐到足底的长度之比是黄金分割比著名的“断臂维纳斯”便是如此若某人的身体满足上述黄金分割比,且身高为,则此人的肚脐到足底的长度可能是______ 精确到.
12. 如图所示,复印纸的型号有,,,,等,它们之间存在着这样一种关系:将其中某一型号如的复印纸沿较长边的中点对折,就能得到两张下一型号的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
13. 如图,已知每个小方格的边长均为,则与的周长比为______.
14. 如图,中,,,,,则的长为______.
15. 如图是一架梯子的示意图,其中,且为使其更稳固,在,间加绑一条安全绳线段量得,则______
16. 下列说法中:所有的等腰三角形都相似;所有的正三角形都相似;所有的正方形都相似;所有的矩形都相似;所有的圆都相似其中说法正确的序号是______ .
17. 如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为,则坝高为
18. 已知,则 ______ .
三、解答题(本大题共8小题,解答应写出文字说明,证明过程或演算步骤)
19. 若,且,求的值.
20. 如图,在的正方形网格中,每个小正方形的边长都是,已知点,,,均为网格线的交点.
在网格中将绕点顺时针旋转,画出旋转后得到的点,,的对应点分别为点,,;
在网格中画出,使∽,且相似比为:点,为格点;
若是线段上的一个动点可以与两端点重合,的面积为,则的取值范围是______ .
21.如图,已知,它们依次交直线、于点、、和点、、,且,.
求的值;
当,时,求的长.
22. 如图,在中,.
求证:;
,,,求的长.
23. 如图,利用标杆测量楼高,点,,在同一直线上,,,垂足分别为,若测得,,,楼高是多少?
24. 如图,在中,,点是边上的一个动点,过点作交点,点为线段的中点,且平分.
求证:∽;
若,,求的长.
25. 如图,每一个小方格正方形的边长均为一个单位长度,的顶点的坐标分别为,,.
请在网格中画出关于原点的中心对称图形.
以点为位似中心,位似比为:,将放大得到,请在网格中画出不要超出方格区域.
求的面积.
26. 青龙寺是西安最著名的樱花观赏地,品种达到了种之多,每年、月陆续开放的樱花让这里成为了花的海洋一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度樱花树四周被围起来了,底部不易到达小明在处竖立了一根标杆,小刚走到处时,站立在处看到标杆顶端和树的顶端在一条直线上此时测得小刚的眼睛到地面的距离;然后,小刚在处蹲下,小明平移标杆到处时,小刚恰好看到标杆顶端和树的顶端在一条直线上,此时测得小刚的眼睛到地面的距离已知,,,点,,,在一条直线上,点在上,,,,根据以上测量过程及测量数据,请你求出这棵樱花树的高度.
答案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
12. 13. : 14. 15. 16. 17. 18.
19. 解:设,
,,,
,
解得,
.
20.
21. 解:,
;
过点作交于,交于,如图,
,,
四边形和四边形都是平行四边形,
,,
,
,
,
,
.
22. 解:,
∽,
,
;
∽,
,
即,解得.
23. 解:,,
,
∽,
,
已知,,,
,
,
答:楼高是.
24. 解:,
,,
∽;
过作交于点,交于点,作交于点、于点,
,,
,
由面积,
,
,
,
,
在中,,
,
,
平分,
,
在中,,
,
是的中点,,
,
,
,
,
.
另解:在中,,
,
,
平分,
,
,
,
点是点到的中点,
,
,
设,
∽,
,
,
解得,
.
25. 解:如图,为所作;
如图,为所作;
的面积.
26. 解:过点作于点,交于点,过点作于点,交于点,
由题意可得:,米,,米,米.
,,
∽,
,
.
,,
∽
.
.
米.
答:这棵樱花树的高度是米.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1. 如果::,::那么:( )
A. : B. : C. : D. :
2. 下面的四个数中能组成比例的是( )
A. 、、和 B. 、、和
C. 、、和 D. 、、和
3. 如图,在中,,,,,则的长为
( )
A. B. C. D.
4. 下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A. B. C. D.
5. 如图,在正方形网格中:、的顶点都在正方形网格的格点上,∽,则的度数为( )
A. B. C. D.
6. 如图,树在路灯的照射下形成投影,已知路灯高,树影,树与路灯的水平距离,则树的高度长是( )
A.
B.
C.
D.
7. 如图,与是位似图形,且位似中心为,::,若的面积为,则的面积为( )
A. B. C. D.
8. 如果,那么的值是( )
A. B. C. D.
9. 如图,是一块矩形场地,宽,长若在其对角线,的延长线上取点,,,,扩建为新的矩形场地,左、右各增加了,上、下各增加了,则的值为( )
A.
B.
C.
D.
10. 如图,在中,,以其三边为边向外作正方形,过点作于点,交线段于点,再过点作分别交边,于点、若矩形的面积为,矩形的面积为,则的长为( )
A.
B.
C.
D.
二、填空题(本大题共8小题)
11. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐到足底的长度之比是黄金分割比著名的“断臂维纳斯”便是如此若某人的身体满足上述黄金分割比,且身高为,则此人的肚脐到足底的长度可能是______ 精确到.
12. 如图所示,复印纸的型号有,,,,等,它们之间存在着这样一种关系:将其中某一型号如的复印纸沿较长边的中点对折,就能得到两张下一型号的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
13. 如图,已知每个小方格的边长均为,则与的周长比为______.
14. 如图,中,,,,,则的长为______.
15. 如图是一架梯子的示意图,其中,且为使其更稳固,在,间加绑一条安全绳线段量得,则______
16. 下列说法中:所有的等腰三角形都相似;所有的正三角形都相似;所有的正方形都相似;所有的矩形都相似;所有的圆都相似其中说法正确的序号是______ .
17. 如图,为了测量山坡的护坡石坝高,把一根长为的竹竿斜靠在石坝旁,量出竿上长为时,它离地面的高度为,则坝高为
18. 已知,则 ______ .
三、解答题(本大题共8小题,解答应写出文字说明,证明过程或演算步骤)
19. 若,且,求的值.
20. 如图,在的正方形网格中,每个小正方形的边长都是,已知点,,,均为网格线的交点.
在网格中将绕点顺时针旋转,画出旋转后得到的点,,的对应点分别为点,,;
在网格中画出,使∽,且相似比为:点,为格点;
若是线段上的一个动点可以与两端点重合,的面积为,则的取值范围是______ .
21.如图,已知,它们依次交直线、于点、、和点、、,且,.
求的值;
当,时,求的长.
22. 如图,在中,.
求证:;
,,,求的长.
23. 如图,利用标杆测量楼高,点,,在同一直线上,,,垂足分别为,若测得,,,楼高是多少?
24. 如图,在中,,点是边上的一个动点,过点作交点,点为线段的中点,且平分.
求证:∽;
若,,求的长.
25. 如图,每一个小方格正方形的边长均为一个单位长度,的顶点的坐标分别为,,.
请在网格中画出关于原点的中心对称图形.
以点为位似中心,位似比为:,将放大得到,请在网格中画出不要超出方格区域.
求的面积.
26. 青龙寺是西安最著名的樱花观赏地,品种达到了种之多,每年、月陆续开放的樱花让这里成为了花的海洋一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度樱花树四周被围起来了,底部不易到达小明在处竖立了一根标杆,小刚走到处时,站立在处看到标杆顶端和树的顶端在一条直线上此时测得小刚的眼睛到地面的距离;然后,小刚在处蹲下,小明平移标杆到处时,小刚恰好看到标杆顶端和树的顶端在一条直线上,此时测得小刚的眼睛到地面的距离已知,,,点,,,在一条直线上,点在上,,,,根据以上测量过程及测量数据,请你求出这棵樱花树的高度.
答案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
12. 13. : 14. 15. 16. 17. 18.
19. 解:设,
,,,
,
解得,
.
20.
21. 解:,
;
过点作交于,交于,如图,
,,
四边形和四边形都是平行四边形,
,,
,
,
,
,
.
22. 解:,
∽,
,
;
∽,
,
即,解得.
23. 解:,,
,
∽,
,
已知,,,
,
,
答:楼高是.
24. 解:,
,,
∽;
过作交于点,交于点,作交于点、于点,
,,
,
由面积,
,
,
,
,
在中,,
,
,
平分,
,
在中,,
,
是的中点,,
,
,
,
,
.
另解:在中,,
,
,
平分,
,
,
,
点是点到的中点,
,
,
设,
∽,
,
,
解得,
.
25. 解:如图,为所作;
如图,为所作;
的面积.
26. 解:过点作于点,交于点,过点作于点,交于点,
由题意可得:,米,,米,米.
,,
∽,
,
.
,,
∽
.
.
米.
答:这棵樱花树的高度是米.
第1页,共1页
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
