第四章 几何图形初步周测试题二(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
19.七年级数学(上)第4章《几何图形初步》周测(二)
一、选择题(每小题3分,共30分)
1.下列图中表示∠CAB的是( )
A. B. C. D.
2.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
3.如图,若∠AOB=∠COD,则( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.∠1与∠2的大小无法比较
4.已知∠α=35°,那么∠α的余角等于( )
A.35° B.55° C.65° D.145°
5.下面等式等式成立的是( )
A.85.5°=83°5′ B.37°12′36″=37.48°
C.24°24′=24.4° D.41.25°=41°25′
6.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中,正确的是( )
A.∠COD=∠AOB B.∠BOC=∠AOB
C.∠AOD=∠AOB D.∠AOD=∠AOB
7.如图,∠AOB=90°,直线CD经过点O,∠AOC=120°,则∠BOD的度数是( )
A.30° B.35° C.40° D.50°
8.如图,在下面的四个等式中,能够表示“OC是∠AOB的平分线”的有( )
①∠AOC=∠BOC;②∠AOC=∠AOB;③∠AOB=2∠BOC;④∠AOC+∠BOC=∠AOB.
A.1个 B.2个 C.3个 D.4个
9.如图,∠AOB是平角,过点 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )O作射线OE,OC,OD,把∠BOE用图中的角表示成两个角或三个角和的形式,能有几种不同的表示方法( )21世纪21世纪教育网有21世纪教育网版权所有
A.2种 B.3种 C.4种 D.5种
10.如图,若两条直线AB,EF相交于点O,∠BOC=α,∠BOF=α,∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),则n的值为( ) 21教育网21cnjy.com
A.2 B.3 C.4 D.5
二、填空题(每小题3分,共18分)
11.如图,∠AOB=90°,以点O为顶点的锐角共有 个.
12.若一个角的补角是126°,则这个角的余角是 度.
13.如图,∠AOB是直角,∠AOC是∠COB的5倍,则∠COB是 .
14.将长方形的纸片ABCD沿AE折叠, ( http: / / www.21cnjy.com )得到如图所示的图形,已知∠CED′=50°.则∠AED的度数为 .21cnjy.com21·cn·jy·com
15.如图,点D在点O的北偏西30°方向,点E在点O的北偏东50°方向,则∠DOE的度数为 .
16.已知∠AOB=80°,过O作射线OC(不同于OA,OB),∠AOC,∠BOC均小于180°,且满足∠AOC=∠BOC,则∠AOC的度数是 .21·cn·jy·comwww.21-cn-jy.com
三、解答题(共8题,共72分)
17.(本题8分)计算:(1)90°-36°38′; (2)23°24′12″×3.
18.(本题8分)如图,已知∠AOB=56°,∠AOC=10°,OD是∠BOC的平分线,求∠BOD的度数.
19.(本题8分)如图,∠AOB=92°,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
20.(本题8分)如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=13°,求∠AOB的度数.
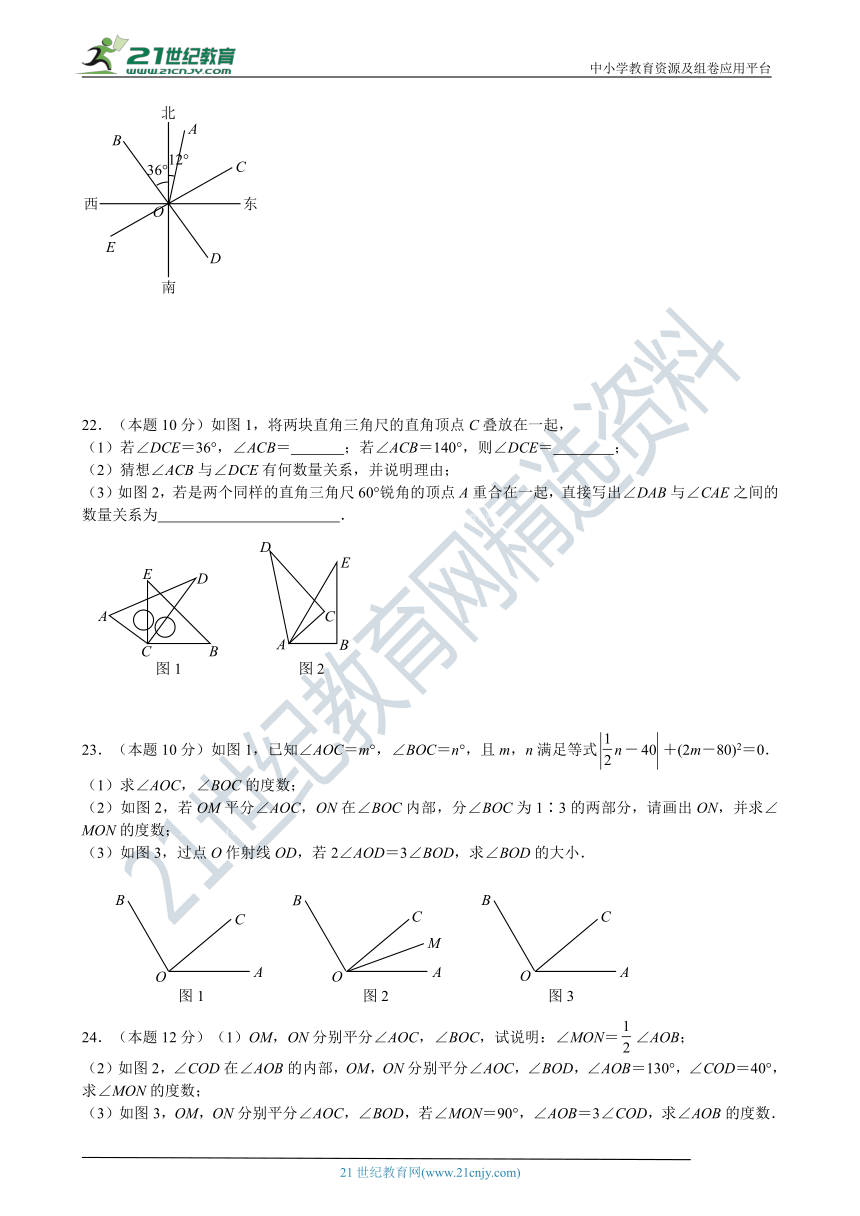
21.(8分)如图,OA的方向是北偏东12°,OB的方向是北偏西36°.
(1)若∠AOC=∠AOB,则OC的方向是北偏东 ;
(2)若OD是OB的反向延长线,则OD的方向是南偏东 ;
(3)在(2)的条件下,OE是OC的反向延长线,求∠AOE的度数.
22.(本题10分)如图1,将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=36°,∠ACB= ;若∠ACB=140°,则∠DCE= ;
(2)猜想∠ACB与∠DCE有何数量关系,并说明理由;
(3)如图2,若是两个同样的直角三角尺 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )60°锐角的顶点A重合在一起,直接写出∠DAB与∠CAE之间的数量关系为 .21世纪教育网21-cn-jy.com21教育网
23.(本题10分)如图1,已知∠AOC=m°,∠BOC=n°,且m,n满足等式+(2m-80)2=0.
(1)求∠AOC,∠BOC的度数;
(2)如图2,若OM平分∠AOC,ON在∠BOC内部,分∠BOC为1∶3的两部分,请画出ON,并求∠MON的度数;2·1·c·n·j·y2·1·c·n·j·y
(3)如图3,过点O作射线OD,若2∠AOD=3∠BOD,求∠BOD的大小.
24.(本题12分)(1)OM,ON分别平分∠AOC,∠BOC,试说明:∠MON=∠AOB;
(2)如图2,∠COD在∠AOB的 ( http: / / www.21cnjy.com )内部,OM,ON分别平分∠AOC,∠BOD,∠AOB=130°,∠COD=40°,求∠MON的度数;【来源:21·世纪·教育·网】【来源:21·世纪·教育·网】
(3)如图3,OM,ON分别平分∠AOC,∠BOD,若∠MON=90°,∠AOB=3∠COD,求∠AOB的度数.
19 七年级数学(上)第4章《几何图形初步》周测(二)
1.A 2.D 3.B 4.B 5.C 6.C 7.A 8.C 9.B
10.B 解:∵∠AOE+∠AOF=∠BOF+∠AOF=180°,∴∠AOE=∠BOF=α.∵∠BOC=α,
∴∠AOC=180°-α,∴∠AOD=∠AOC=,
∴∠DOE=∠AOD+∠AOE=+α=,∴α=α,∴n=3.
11.5 12.36 13.15 14.65° 15.80°
16.30°或105° 解:若OC在∠AOB内部,则∠AOC=×80°=30°,若OC在∠AOB的外部,
则∠AOC=×280°=105°.
17.解:(1)53°22′;(2)70°12′36″.
18.解:∠BOD=23°.
19.解:∠EOD=∠AOB=46°.
20.解:∠AOB=26°.
21.解:(1)60°;
(2)36°;
(3)∠AOC=60°-12°=48°,∠AOE=180°-48°=132°.
22.解:(1)144°;40°;
(2)∠ACB+∠DCE=180°,理由略;
(3)∠DAB+∠CAE=120°.
23.解:(1)∠AOC=40°,∠BOC=80°;
(2)图略,∠MON=40°或80°;
(3)设∠BOD=x°,则∠AOD=x°,
当OD在区域①时,x+x=120,解得x=48,此时∠BOD=48°;当OD在区域②时,x-x=120,解得x=240,此时∠BOD=240°(舍);当OD在区域③时,x+x+120=360,解得x=96,此时
∠BOD=96°;当OD在区域④时,∠AOD<∠BOD,不含题意;
∴在区域②④时,不存在OD,使2∠AOD=3∠BOD,综上所述,∠BOD=96°或48°
24.解:(1)略
(2)∠MON=(∠AOB+∠COD)=×170°=85°
(3)设∠BDN=∠DON=x,∠AOM=∠COM=y,
∵∠MON=90°,∴x+y+∠COD=90°,又∵∠AOB=2x+2y+∠COD=3∠COD,
∴x+y=∠COD,∴2∠COD=90°,∠COD=45°,∴x+y=45°,∴∠AOB=135°.
( http: / / www.21cnjy.com )
A
C
B
A
B
C
A
B
C
D
A
C
D
A
D
B
C
O
1
2
A
C
D
B
O
A
O
B
D
C
A
C
B
O
O
A
B
D
C
E
A
F
B
C
E
D
O
A
D
C
B
O
A
O
C
B
A
B
C
D
E
D′
A
O
B
东
西
北
D
E
A
C
D
B
O
O
A
E
C
D
B
O
A
B
D
C
36°
12°
A
C
东
北
B
西
南
O
E
D
D
C
E
B
A
C
B
D
E
A
图1
图2
O
A
A
A
O
O
B
C
M
B
C
C
B
图1
图2
图3
O
B
C
A
图1
图3
N
M
B
O
A
C
N
图2
D
M
B
O
A
C
N
D
M
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
19.七年级数学(上)第4章《几何图形初步》周测(二)
一、选择题(每小题3分,共30分)
1.下列图中表示∠CAB的是( )
A. B. C. D.
2.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
3.如图,若∠AOB=∠COD,则( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.∠1与∠2的大小无法比较
4.已知∠α=35°,那么∠α的余角等于( )
A.35° B.55° C.65° D.145°
5.下面等式等式成立的是( )
A.85.5°=83°5′ B.37°12′36″=37.48°
C.24°24′=24.4° D.41.25°=41°25′
6.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中,正确的是( )
A.∠COD=∠AOB B.∠BOC=∠AOB
C.∠AOD=∠AOB D.∠AOD=∠AOB
7.如图,∠AOB=90°,直线CD经过点O,∠AOC=120°,则∠BOD的度数是( )
A.30° B.35° C.40° D.50°
8.如图,在下面的四个等式中,能够表示“OC是∠AOB的平分线”的有( )
①∠AOC=∠BOC;②∠AOC=∠AOB;③∠AOB=2∠BOC;④∠AOC+∠BOC=∠AOB.
A.1个 B.2个 C.3个 D.4个
9.如图,∠AOB是平角,过点 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )O作射线OE,OC,OD,把∠BOE用图中的角表示成两个角或三个角和的形式,能有几种不同的表示方法( )21世纪21世纪教育网有21世纪教育网版权所有
A.2种 B.3种 C.4种 D.5种
10.如图,若两条直线AB,EF相交于点O,∠BOC=α,∠BOF=α,∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),则n的值为( ) 21教育网21cnjy.com
A.2 B.3 C.4 D.5
二、填空题(每小题3分,共18分)
11.如图,∠AOB=90°,以点O为顶点的锐角共有 个.
12.若一个角的补角是126°,则这个角的余角是 度.
13.如图,∠AOB是直角,∠AOC是∠COB的5倍,则∠COB是 .
14.将长方形的纸片ABCD沿AE折叠, ( http: / / www.21cnjy.com )得到如图所示的图形,已知∠CED′=50°.则∠AED的度数为 .21cnjy.com21·cn·jy·com
15.如图,点D在点O的北偏西30°方向,点E在点O的北偏东50°方向,则∠DOE的度数为 .
16.已知∠AOB=80°,过O作射线OC(不同于OA,OB),∠AOC,∠BOC均小于180°,且满足∠AOC=∠BOC,则∠AOC的度数是 .21·cn·jy·comwww.21-cn-jy.com
三、解答题(共8题,共72分)
17.(本题8分)计算:(1)90°-36°38′; (2)23°24′12″×3.
18.(本题8分)如图,已知∠AOB=56°,∠AOC=10°,OD是∠BOC的平分线,求∠BOD的度数.
19.(本题8分)如图,∠AOB=92°,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
20.(本题8分)如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=13°,求∠AOB的度数.
21.(8分)如图,OA的方向是北偏东12°,OB的方向是北偏西36°.
(1)若∠AOC=∠AOB,则OC的方向是北偏东 ;
(2)若OD是OB的反向延长线,则OD的方向是南偏东 ;
(3)在(2)的条件下,OE是OC的反向延长线,求∠AOE的度数.
22.(本题10分)如图1,将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=36°,∠ACB= ;若∠ACB=140°,则∠DCE= ;
(2)猜想∠ACB与∠DCE有何数量关系,并说明理由;
(3)如图2,若是两个同样的直角三角尺 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )60°锐角的顶点A重合在一起,直接写出∠DAB与∠CAE之间的数量关系为 .21世纪教育网21-cn-jy.com21教育网
23.(本题10分)如图1,已知∠AOC=m°,∠BOC=n°,且m,n满足等式+(2m-80)2=0.
(1)求∠AOC,∠BOC的度数;
(2)如图2,若OM平分∠AOC,ON在∠BOC内部,分∠BOC为1∶3的两部分,请画出ON,并求∠MON的度数;2·1·c·n·j·y2·1·c·n·j·y
(3)如图3,过点O作射线OD,若2∠AOD=3∠BOD,求∠BOD的大小.
24.(本题12分)(1)OM,ON分别平分∠AOC,∠BOC,试说明:∠MON=∠AOB;
(2)如图2,∠COD在∠AOB的 ( http: / / www.21cnjy.com )内部,OM,ON分别平分∠AOC,∠BOD,∠AOB=130°,∠COD=40°,求∠MON的度数;【来源:21·世纪·教育·网】【来源:21·世纪·教育·网】
(3)如图3,OM,ON分别平分∠AOC,∠BOD,若∠MON=90°,∠AOB=3∠COD,求∠AOB的度数.
19 七年级数学(上)第4章《几何图形初步》周测(二)
1.A 2.D 3.B 4.B 5.C 6.C 7.A 8.C 9.B
10.B 解:∵∠AOE+∠AOF=∠BOF+∠AOF=180°,∴∠AOE=∠BOF=α.∵∠BOC=α,
∴∠AOC=180°-α,∴∠AOD=∠AOC=,
∴∠DOE=∠AOD+∠AOE=+α=,∴α=α,∴n=3.
11.5 12.36 13.15 14.65° 15.80°
16.30°或105° 解:若OC在∠AOB内部,则∠AOC=×80°=30°,若OC在∠AOB的外部,
则∠AOC=×280°=105°.
17.解:(1)53°22′;(2)70°12′36″.
18.解:∠BOD=23°.
19.解:∠EOD=∠AOB=46°.
20.解:∠AOB=26°.
21.解:(1)60°;
(2)36°;
(3)∠AOC=60°-12°=48°,∠AOE=180°-48°=132°.
22.解:(1)144°;40°;
(2)∠ACB+∠DCE=180°,理由略;
(3)∠DAB+∠CAE=120°.
23.解:(1)∠AOC=40°,∠BOC=80°;
(2)图略,∠MON=40°或80°;
(3)设∠BOD=x°,则∠AOD=x°,
当OD在区域①时,x+x=120,解得x=48,此时∠BOD=48°;当OD在区域②时,x-x=120,解得x=240,此时∠BOD=240°(舍);当OD在区域③时,x+x+120=360,解得x=96,此时
∠BOD=96°;当OD在区域④时,∠AOD<∠BOD,不含题意;
∴在区域②④时,不存在OD,使2∠AOD=3∠BOD,综上所述,∠BOD=96°或48°
24.解:(1)略
(2)∠MON=(∠AOB+∠COD)=×170°=85°
(3)设∠BDN=∠DON=x,∠AOM=∠COM=y,
∵∠MON=90°,∴x+y+∠COD=90°,又∵∠AOB=2x+2y+∠COD=3∠COD,
∴x+y=∠COD,∴2∠COD=90°,∠COD=45°,∴x+y=45°,∴∠AOB=135°.
( http: / / www.21cnjy.com )
A
C
B
A
B
C
A
B
C
D
A
C
D
A
D
B
C
O
1
2
A
C
D
B
O
A
O
B
D
C
A
C
B
O
O
A
B
D
C
E
A
F
B
C
E
D
O
A
D
C
B
O
A
O
C
B
A
B
C
D
E
D′
A
O
B
东
西
北
D
E
A
C
D
B
O
O
A
E
C
D
B
O
A
B
D
C
36°
12°
A
C
东
北
B
西
南
O
E
D
D
C
E
B
A
C
B
D
E
A
图1
图2
O
A
A
A
O
O
B
C
M
B
C
C
B
图1
图2
图3
O
B
C
A
图1
图3
N
M
B
O
A
C
N
图2
D
M
B
O
A
C
N
D
M
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
