第四章 几何图形初步专题卷A——单元核心考点归纳一点通(含答案)
文档属性
| 名称 | 第四章 几何图形初步专题卷A——单元核心考点归纳一点通(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
20.七年级数学(上)第4章《几何图形初步》专题卷A——单元核心考点归纳一点通
核心考点1 本章核心概念
(一)平面图形与立体图形
1.图中的几何体是由哪个平面图形绕虚线旋转一周得到的( )
A. B. C. D. 21世纪教育网版权所有
(二)直线、射线、线段
2.下列说法中,正确的是( )
A.射线AB和射线BA是同一条射线
B.射线就是直线
C.延长直线AB
D.经过两点有一条直线,并且只有一条直线
(三)线段的中点
3.如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
A.2cm B.3cm C.4cm D.6cm21cnjy.com
(四)角
4.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A. B. C. D.
(五)角平分线
5.如图,点O在直线AB上,射线OC平分∠DOB,若∠AOD=110°,则
∠BOC等于( )
A.35° B,70°
C.110° D.145°
(六)余角、补角
6.一个角的余角是这个角的补角的,则这个角的度数是( )
A.30° B.45° C.60° D.70°www.21-cn-jy.com
核心考点2 直线、射线、线段的计数
7.直线l上有A、B、C、D、E五点,则直线l上的射线有多少条?线段有多少条?
8.直线l上有n个点,则直线l的射线有多少条?线段有多少条?
9.如图,AB=BC=CD=DE=EF=2,求图中所有线段的和.
核心考点3 本章核心性质
(一)直线的性质:两点确定一条直线
10.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )【来源:21·世纪·教育·网】
A.两点确定一条直线
B.两点之间线段最短
C.两点确定一条线段
D.两点之间,直线最短
(二)线段的性质:两点之间,线段最短
11.“把弯曲的河道该直,就能缩短路程”,其中蕴含的数学道理是( )
A.两点之间线段最短 B.直线比曲线短
C.两点之间直线最短 D.两点确定一条直线
(三)余角和补角的性质:同角(等角)的余角(补角)相等
12.如图,∠AOC=∠BOD=90°,下面结论中,正确的是( )
①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③∠BOC+∠AOD=180°;
④∠AOC-∠COD=∠BOC.
A.①②③ B.①②④ C.①③④ D.②③④2-1-c-n-j-y
核心考点4 线段的和、差、倍、分
13.如图,A、B、C、D是直线l上顺次四点,M、N分别是AB、CD的中点,且MN=6,BC=1,求AD的长.
14.如图,延长线段AB至点C,使BC=AB,反向延长AB至点D,使AD=AB.
(1)依题意画出图形,则=_______________(直接写出结果);
(2)若点E为BC的中点,且BD-2BE=10,求AB的长.
核心考点5 角的和、差、倍、分
15.如图,已知∠AOB=120°,OC平分∠AOB,OD、OE分别平分∠AOC、∠COB,求∠DOE的度数.
16.如图,已知OB平分∠AOC,OD平分∠COE,∠AOD=110°,∠BOE=100°,求∠AOE的度数.
核心考点6 本章核心思想方法
(一)整体思想
17.如图,在同一直线上有四点A、B、C、D,已知AD=DB,AC=CB,且CD=4,求AB的长.
18.如图,∠AOC比∠BOC小30°,∠AOD=∠BOD,求∠DOC的度数.
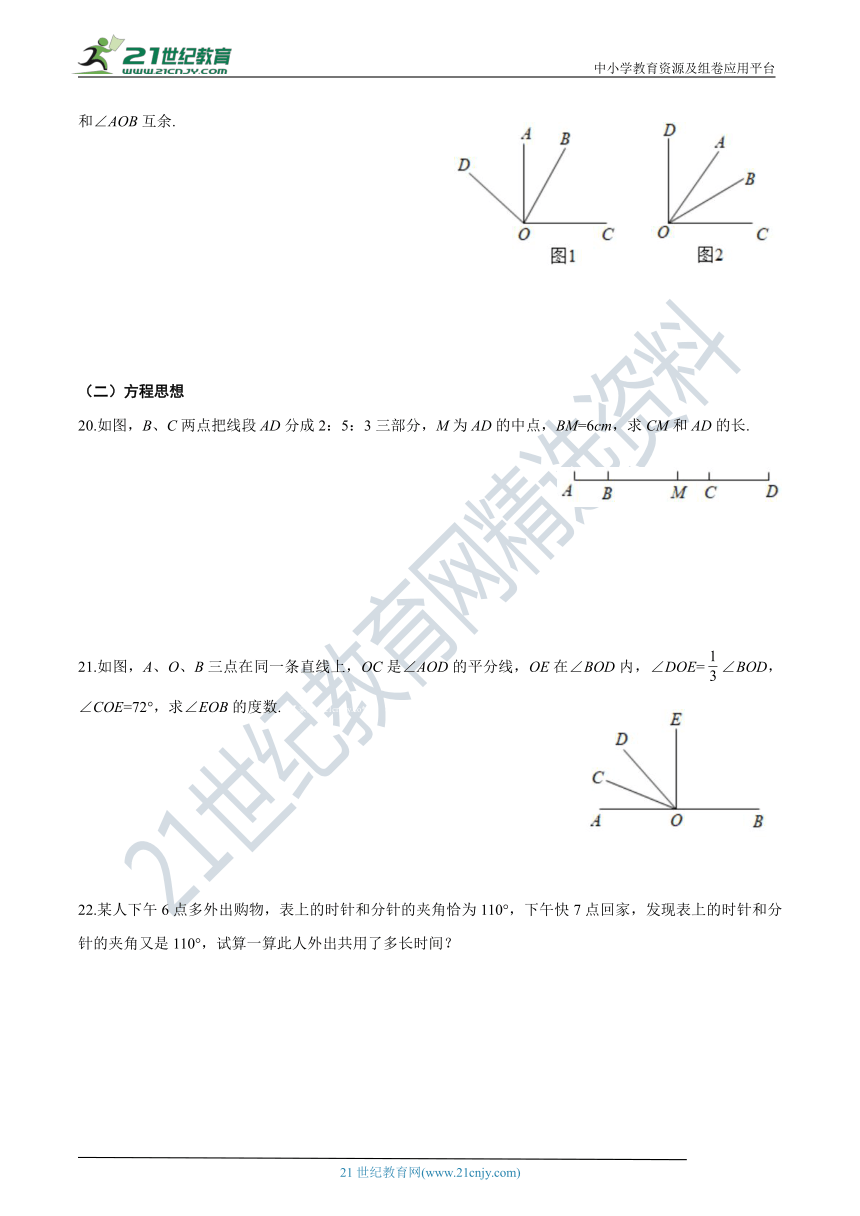
19.已知∠AOC=∠BOD=(0°<<180°).
(1)如图1,若=90°,
①写出图中一组相等的角(除直角外)___________________,理由是____________________;
②试猜想∠COD和∠AOB在数量上是相等、互余,还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是____________________;当=__________,∠COD 和∠AOB互余.2·1·c·n·j·y
(二)方程思想
20.如图,B、C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
21.如图,A、O、B三点在同一条直线上,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=∠BOD,∠COE=72°,求∠EOB的度数. 【来源:21cnj*y.co*m】
22.某人下午6点多外出购物,表上的时针 ( http: / / www.21cnjy.com )和分针的夹角恰为110°,下午快7点回家,发现表上的时针和分针的夹角又是110°,试算一算此人外出共用了多长时间?21教育网
(三)分类讨论思想
23.数轴上有A、B两点,它们对应的数分别为-8和22,数轴上有另外一点C,且AC:BC=1:4,求点C在数轴上对应的数.21*cnjy*com
24.已知∠AOB=80°,同一平面内有射线OC、OD,若∠AOC=20°,∠BOD=30°,求∠COD的度数.
25.已知线段AB=12,在AB上有C、D、M、N四点,且AC:CD:DB=1:2:3,AM=AC,DN=DB,求线段MN的长.21·cn·jy·com
20七年数学(上)第4章《几何形初步》专題卷A--单元核心考点归纳一点通
1.C 2.D 3.B 4.A 5.A 6.C
7解:直线上有10条射,线段有10条,
8.解:直线上有2n条射线,线段有 条
9.解:(2+4+6+8+10)+(2+4+6+8)+(2+4+6)+(2+4)+2=7021.解:∠EOB-72
10.A 11.A 12.C
13.解:由线段的和差,得MB+CN=MN-BC=6-1=5由M,N分别是AB,CD的中点,
得AB=2MB,CD=2CN,
AB+CD=2(MB+CN)=2×5=10,由线段的和差,得AD=AB+BC+CD=10+1=11.
14.:(1)画图略,∵BC=AB,AD=AB,∴
(2)∵E是BC的中点,∴BC=2BE=AB,∵BD-2BE=10,
∴AB+AB-AB=10,解得AB=12.
15.解:∵∠AOB=120°,OC平分∠AOB,∴∠AOC=∠COB=∠AOB=60°
∵OD,OE分别平分∠AOC,∠COB,∴∠COD=∠AOC=30°,∠COE=∠COB=30°
∴∠DOE=∠COD+∠COE=30°+30°=60°
16.解:∵OB平分∠AOC,OD平分∠COE,∴∠EOD=∠DOC= x°,∠AOB=∠COB,
∵∠AOD=110°,∠BOE=100°,∴∠AOB=∠BOC=100°-2x°,
∴∠COD+∠COB+∠AOB=110°,∴x+100-2x+100-2x=110,x=30,即∠EOD=∠DOC=30°
∠AOE=∠AOD+∠DOE=110°+30°=140°.
17.解:设DB=x,则AD=x,AC=x ,∵AC=CB,∴AC=AB=
CB=AB=∴CD=DB-CB= ∵CD=4,∴ ,解得x=9 , AB=
18.∠DOC=15°.
19.解:(1)①∠AOD=∠BOC,同角的余角相等;②∠COD和∠AOB互补,说明理由略;
(2)∠COD+∠AOB=2∠AOC,若∠COD和∠AOB互余,则2∠AOC=90°,
所以∠AOC=45°,即ɑ=45°.
20.解:设AB=2 xcm,BC=5xcm,CD=3xcm,所以AD=AB+BC+CD=10xcm,21·世纪*教育网
因为M是AD的中点,所以AM=MD=5xcm,所以BM=AM-AB=5x-2x=3xcm,
因为BM=6cm,所以3x=6,x=2,故CM=MD-CD=5x-3x=2x=4(cm)
AD=10x=10×2=20(cm)
21.解:∠EOB=72°.
22.方法一:设时针从此人外出到回家走了x°,则分针走了2×110°+x°=220°+x°
由题意,得解得x=20,则(小时),即此人外出共用了40分钟
方法二:分针一分钟走6度,即分针的 ( http: / / www.21cnjy.com )角度是6度/分,时针一分钟走0.5度,即时针的角速度是0.5度/分,开始时分针在时针后面110度,后来分针在时针前面110度,www-2-1-cnjy-com
这是一个追及问题.设共用了x分钟,由题意得(6-0.5)x==110+110,解得x=40.
即此人外出共用了40分钟.
23.解:①当点C在线段AB上时,AC=AB/5=6,则点C所对应的数是-8+6=- 2;
②当点C在线段AB的反向延长线上时,AC=AB/3=10,则点C所对应的数是-8+(-10)=- 18.
24.解∠COD=30°或70°或90°或130°.
25.解:因为AB=12,AC:CD:DB=1:2:3,所以AC=
CD=DB=AB=12×=6,因为AM=AC,DN=DB,
所以MC=AC=1,DN=DB=6×
①当点N在点侧右时,如答图①,MN=MC+CD+DN=1+4+
②当点N在点D左侧时,如答图②,MN=MC+CD-DN=1+4-=.综上所述,线段MN的长为或.【出处:21教育名师】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
20.七年级数学(上)第4章《几何图形初步》专题卷A——单元核心考点归纳一点通
核心考点1 本章核心概念
(一)平面图形与立体图形
1.图中的几何体是由哪个平面图形绕虚线旋转一周得到的( )
A. B. C. D. 21世纪教育网版权所有
(二)直线、射线、线段
2.下列说法中,正确的是( )
A.射线AB和射线BA是同一条射线
B.射线就是直线
C.延长直线AB
D.经过两点有一条直线,并且只有一条直线
(三)线段的中点
3.如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
A.2cm B.3cm C.4cm D.6cm21cnjy.com
(四)角
4.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A. B. C. D.
(五)角平分线
5.如图,点O在直线AB上,射线OC平分∠DOB,若∠AOD=110°,则
∠BOC等于( )
A.35° B,70°
C.110° D.145°
(六)余角、补角
6.一个角的余角是这个角的补角的,则这个角的度数是( )
A.30° B.45° C.60° D.70°www.21-cn-jy.com
核心考点2 直线、射线、线段的计数
7.直线l上有A、B、C、D、E五点,则直线l上的射线有多少条?线段有多少条?
8.直线l上有n个点,则直线l的射线有多少条?线段有多少条?
9.如图,AB=BC=CD=DE=EF=2,求图中所有线段的和.
核心考点3 本章核心性质
(一)直线的性质:两点确定一条直线
10.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )【来源:21·世纪·教育·网】
A.两点确定一条直线
B.两点之间线段最短
C.两点确定一条线段
D.两点之间,直线最短
(二)线段的性质:两点之间,线段最短
11.“把弯曲的河道该直,就能缩短路程”,其中蕴含的数学道理是( )
A.两点之间线段最短 B.直线比曲线短
C.两点之间直线最短 D.两点确定一条直线
(三)余角和补角的性质:同角(等角)的余角(补角)相等
12.如图,∠AOC=∠BOD=90°,下面结论中,正确的是( )
①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③∠BOC+∠AOD=180°;
④∠AOC-∠COD=∠BOC.
A.①②③ B.①②④ C.①③④ D.②③④2-1-c-n-j-y
核心考点4 线段的和、差、倍、分
13.如图,A、B、C、D是直线l上顺次四点,M、N分别是AB、CD的中点,且MN=6,BC=1,求AD的长.
14.如图,延长线段AB至点C,使BC=AB,反向延长AB至点D,使AD=AB.
(1)依题意画出图形,则=_______________(直接写出结果);
(2)若点E为BC的中点,且BD-2BE=10,求AB的长.
核心考点5 角的和、差、倍、分
15.如图,已知∠AOB=120°,OC平分∠AOB,OD、OE分别平分∠AOC、∠COB,求∠DOE的度数.
16.如图,已知OB平分∠AOC,OD平分∠COE,∠AOD=110°,∠BOE=100°,求∠AOE的度数.
核心考点6 本章核心思想方法
(一)整体思想
17.如图,在同一直线上有四点A、B、C、D,已知AD=DB,AC=CB,且CD=4,求AB的长.
18.如图,∠AOC比∠BOC小30°,∠AOD=∠BOD,求∠DOC的度数.
19.已知∠AOC=∠BOD=(0°<<180°).
(1)如图1,若=90°,
①写出图中一组相等的角(除直角外)___________________,理由是____________________;
②试猜想∠COD和∠AOB在数量上是相等、互余,还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是____________________;当=__________,∠COD 和∠AOB互余.2·1·c·n·j·y
(二)方程思想
20.如图,B、C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
21.如图,A、O、B三点在同一条直线上,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=∠BOD,∠COE=72°,求∠EOB的度数. 【来源:21cnj*y.co*m】
22.某人下午6点多外出购物,表上的时针 ( http: / / www.21cnjy.com )和分针的夹角恰为110°,下午快7点回家,发现表上的时针和分针的夹角又是110°,试算一算此人外出共用了多长时间?21教育网
(三)分类讨论思想
23.数轴上有A、B两点,它们对应的数分别为-8和22,数轴上有另外一点C,且AC:BC=1:4,求点C在数轴上对应的数.21*cnjy*com
24.已知∠AOB=80°,同一平面内有射线OC、OD,若∠AOC=20°,∠BOD=30°,求∠COD的度数.
25.已知线段AB=12,在AB上有C、D、M、N四点,且AC:CD:DB=1:2:3,AM=AC,DN=DB,求线段MN的长.21·cn·jy·com
20七年数学(上)第4章《几何形初步》专題卷A--单元核心考点归纳一点通
1.C 2.D 3.B 4.A 5.A 6.C
7解:直线上有10条射,线段有10条,
8.解:直线上有2n条射线,线段有 条
9.解:(2+4+6+8+10)+(2+4+6+8)+(2+4+6)+(2+4)+2=7021.解:∠EOB-72
10.A 11.A 12.C
13.解:由线段的和差,得MB+CN=MN-BC=6-1=5由M,N分别是AB,CD的中点,
得AB=2MB,CD=2CN,
AB+CD=2(MB+CN)=2×5=10,由线段的和差,得AD=AB+BC+CD=10+1=11.
14.:(1)画图略,∵BC=AB,AD=AB,∴
(2)∵E是BC的中点,∴BC=2BE=AB,∵BD-2BE=10,
∴AB+AB-AB=10,解得AB=12.
15.解:∵∠AOB=120°,OC平分∠AOB,∴∠AOC=∠COB=∠AOB=60°
∵OD,OE分别平分∠AOC,∠COB,∴∠COD=∠AOC=30°,∠COE=∠COB=30°
∴∠DOE=∠COD+∠COE=30°+30°=60°
16.解:∵OB平分∠AOC,OD平分∠COE,∴∠EOD=∠DOC= x°,∠AOB=∠COB,
∵∠AOD=110°,∠BOE=100°,∴∠AOB=∠BOC=100°-2x°,
∴∠COD+∠COB+∠AOB=110°,∴x+100-2x+100-2x=110,x=30,即∠EOD=∠DOC=30°
∠AOE=∠AOD+∠DOE=110°+30°=140°.
17.解:设DB=x,则AD=x,AC=x ,∵AC=CB,∴AC=AB=
CB=AB=∴CD=DB-CB= ∵CD=4,∴ ,解得x=9 , AB=
18.∠DOC=15°.
19.解:(1)①∠AOD=∠BOC,同角的余角相等;②∠COD和∠AOB互补,说明理由略;
(2)∠COD+∠AOB=2∠AOC,若∠COD和∠AOB互余,则2∠AOC=90°,
所以∠AOC=45°,即ɑ=45°.
20.解:设AB=2 xcm,BC=5xcm,CD=3xcm,所以AD=AB+BC+CD=10xcm,21·世纪*教育网
因为M是AD的中点,所以AM=MD=5xcm,所以BM=AM-AB=5x-2x=3xcm,
因为BM=6cm,所以3x=6,x=2,故CM=MD-CD=5x-3x=2x=4(cm)
AD=10x=10×2=20(cm)
21.解:∠EOB=72°.
22.方法一:设时针从此人外出到回家走了x°,则分针走了2×110°+x°=220°+x°
由题意,得解得x=20,则(小时),即此人外出共用了40分钟
方法二:分针一分钟走6度,即分针的 ( http: / / www.21cnjy.com )角度是6度/分,时针一分钟走0.5度,即时针的角速度是0.5度/分,开始时分针在时针后面110度,后来分针在时针前面110度,www-2-1-cnjy-com
这是一个追及问题.设共用了x分钟,由题意得(6-0.5)x==110+110,解得x=40.
即此人外出共用了40分钟.
23.解:①当点C在线段AB上时,AC=AB/5=6,则点C所对应的数是-8+6=- 2;
②当点C在线段AB的反向延长线上时,AC=AB/3=10,则点C所对应的数是-8+(-10)=- 18.
24.解∠COD=30°或70°或90°或130°.
25.解:因为AB=12,AC:CD:DB=1:2:3,所以AC=
CD=DB=AB=12×=6,因为AM=AC,DN=DB,
所以MC=AC=1,DN=DB=6×
①当点N在点侧右时,如答图①,MN=MC+CD+DN=1+4+
②当点N在点D左侧时,如答图②,MN=MC+CD-DN=1+4-=.综上所述,线段MN的长为或.【出处:21教育名师】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
