第四章 几何图形初步专题卷B——综合题探究(选用)(含答案)
文档属性
| 名称 | 第四章 几何图形初步专题卷B——综合题探究(选用)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 11:26:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
21.七年级数学(上)第4章《几何图形初步》专题卷B——综合题探究(选用)
综合探究一 线段上的单动点问题
1.数轴上有A,B两点,点A对应的数为a,点B对应的数为b,且a,b满足|a+10|+(b-2)2=0.
(1)请直接写出a= ,b= .
(2)若点C在线段AB之间,数轴上一动点D在点C的右侧移动,若AC=2BD,CD=n.求点D在数轴
上对应的数(用含n的式子表示).
综合探究二 线段上的双动点问题
2.如图,已知O为原点,点A,B,C是数轴上三点,且AB=3BC,点C对应的数为6,线段BC=4.
(1)直接写出点A对应的数为 ,点B对应的数为 ;
(2)动点P,Q同时从A,C两点出发,分别以每秒4个单位长度和每秒2个单位长度的速度沿数轴正
正半轴方向运动. M为AP中点,点N在CQ上,且CQ=3CN,设P,Q两点运动的时间为t秒.
①请用含t的代数式分别表示出点M和点N两点所对应的数;
②请问当t为何值时,OM=2BN?
综合探究三 线段的定值问题
3.在数轴上有A,B两点,点A对应的数为a,点B对应的数为b,且a,b满足|a+4|+(b-8)2=0.
(1)求线段AB的长;
(2)若点N从点A出发以3个单位长度/秒的速度向右运动,同时点M从B点出发以1个单位长度/秒
的速度向右运动;且D为MN的中点,E为DM的中点,若N在AB之间运动时,在DN之间始
终有一点Q使得EQ=3,试说明为定值.
综合探究四 角与单动线问题
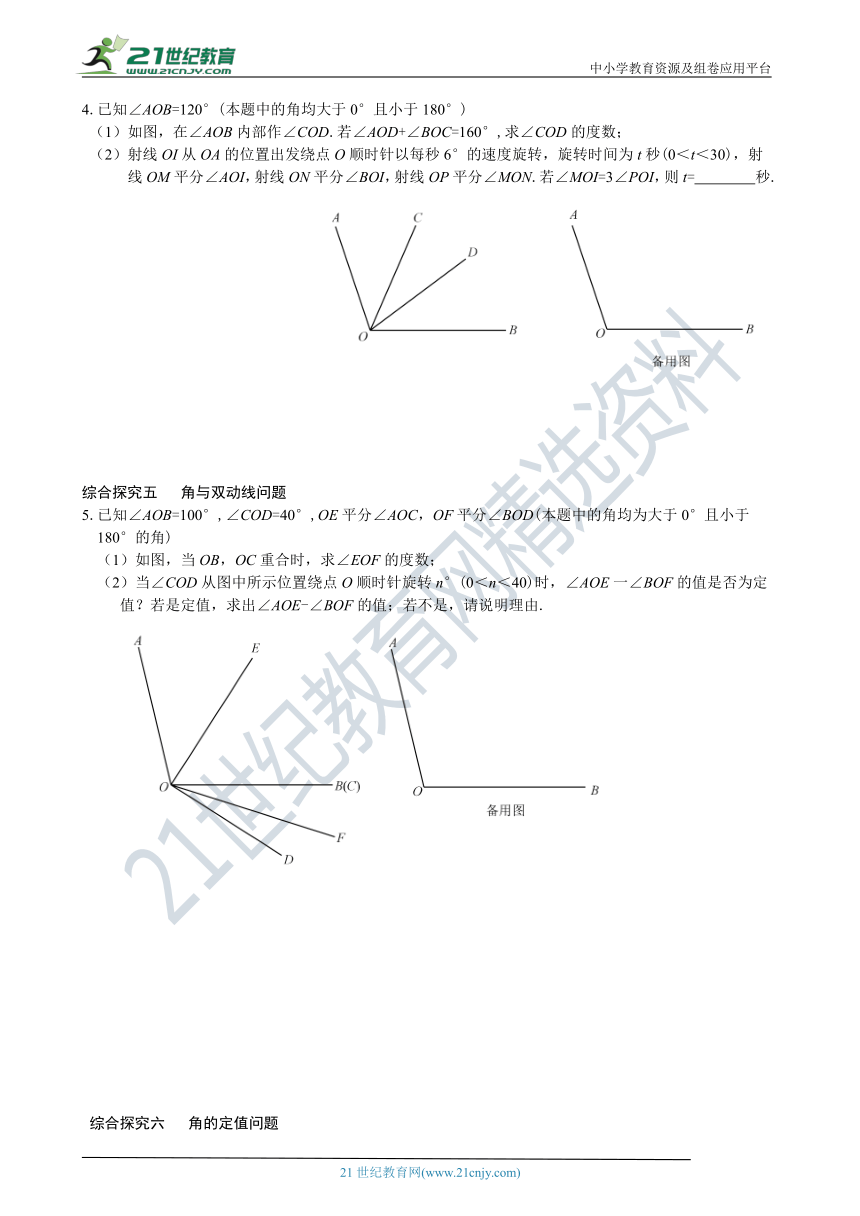
4.已知∠AOB=120°(本题中的角均大于0°且小于180°)
(1)如图,在∠AOB内部作∠COD.若∠AOD+∠BOC=160°,求∠COD的度数;
(2)射线OI从OA的位置出发绕点O顺时针以每秒6°的速度旋转,旋转时间为t秒(0<t<30),射
线OM平分∠AOI,射线ON平分∠BOI,射线OP平分∠MON.若∠MOI=3∠POI,则t= 秒.
( http: / / www.21cnjy.com )
综合探究五 角与双动线问题
5.已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD(本题中的角均为大于0°且小于
180°的角)
(1)如图,当OB,OC重合时,求∠EOF的度数;
(2)当∠COD从图中所示位置绕点O顺时针旋转n°(0<n<40)时,∠AOE一∠BOF的值是否为定
值?若是定值,求出∠AOE-∠BOF的值;若不是,请说明理由.
( http: / / www.21cnjy.com )
综合探究六 角的定值问题
6.如图,两条直线AB,CD相交于点O,且∠AOC=∠AOD,射线OM从OB开始绕O点逆时针方向旋
转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s运动时间为t秒,(0<t<6,本题中的角均小于平角)21世纪教育网版权所有
(1)当t=2时,∠MON的度数为 ,∠BON的度数为 ;
(2)如图2,当射线OM在∠COB内部,是定值时,求t的取值范围,求这个定]
值.
( http: / / www.21cnjy.com )
21 七年级数学(上)第4章《几何图形初步》专题卷B——综合题探究(选用)
1.解:(1)a=-10,b=2;
(2)①当点D在B左侧时,设BD=x,则AC=2x,∴2x+x+n=12,得:x=4-,此时点D对应的数为2-(4-)=-2;21教育网
②当点D在B右侧时,设BD=x,则AC=2x,∴2x+n-x=12,得:x=12-n,此时点D对应的数为2+(12-n)=14-n.21cnjy.com
2.解:(1)点B对应的数为2,点A对应的数为-10;
(2)①运动t秒后,AP=4t,CQ=2t,∴AM=×4t=2t,点M在点A右侧,点M对应的数为21t-10;∵CN=×2t=t,点N在点C右侧,∴点N对应的数为t+6;21·cn·jy·com
②由①知,点M对应的数为(2t-10),N对应的数为(t+6),当t≤5时,OM=0-(2t-10)=10-2t,BN=(t+6)-2=t+4,由OM=2BN得,10-2t=2(t+4),解得t=;www.21-cn-jy.com
当t>5时,OM=2t-10,BN=t+6-2=t+4,由OM=2BN得,2t-10=2(t+4),解得t=27,综合上述,当t为秒或27秒时,OM=2BN.2·1·c·n·j·y
3.解:(1)a=-4,b=8,AB=12;
(2)设运动时间为t秒,运动t秒后点N对应的数为3t-4,点M对应的数为t+8,点D对应的数为2+2t,点E对应的t+5,N在AB间运动时,-4<3t-4<8,得0<t<4,∴-3t-4<2t+2<t+5<t+8,知点N,点D在点E的左侧,即点Q在点E的左侧,∴点Q对应的数为t+5-3=t+2,∴NQ=t+2-(3t-4)=6-t,NB=8-(3t-4)=12-3t,∴=,为定值.【来源:21·世纪·教育·网】
4.解:(1)∠COD=∠AOD+∠BOC-∠AOB=160°-120°=40°;
(2)7.5或15.设旋转n°,对于∠IOM,当0<n<180时,∠IOM=;当180<n<300时,∠IOM=180°-.对于∠POI,当0<n<60时,∠POI=30°-;当60<n<180时,∠POI=-30°.
分两种情况:①0<n<60,=(30-)×3,n=45,t=7.5;
②60<n<180,=(-30)×3,n=90,t=15.
5.解:(1)∠EOF=∠AOD=(∠AOB+∠COD)=70°;
(2)设∠AOE=∠COE=x,∠BO ( http: / / www.21cnjy.com )F=∠DOF=y°,∴∠BOC=2y-40°,∴∠AOB=∠AOC-∠BOC=2x-2y+40°=140°,x-y=30°,∴∠AOE-∠BOF=x-y=30°为定值.21·世纪*教育网
6.解:(1)144°;114°;
(2)当∠MON为平角时,t=,
①当0<t<时,∠COM=(90-15t)°,∠BON=(90+12t)°,∠MON=(90+15t+12t)°;∴==,不是定值;www-2-1-cnjy-com
②∵≤t<6,∠COM=(90-15t)°,∠BON=(90+12t)°,∠MON=(270-27t)°,2-1-c-n-j-y
∴==,=3,为定值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
21.七年级数学(上)第4章《几何图形初步》专题卷B——综合题探究(选用)
综合探究一 线段上的单动点问题
1.数轴上有A,B两点,点A对应的数为a,点B对应的数为b,且a,b满足|a+10|+(b-2)2=0.
(1)请直接写出a= ,b= .
(2)若点C在线段AB之间,数轴上一动点D在点C的右侧移动,若AC=2BD,CD=n.求点D在数轴
上对应的数(用含n的式子表示).
综合探究二 线段上的双动点问题
2.如图,已知O为原点,点A,B,C是数轴上三点,且AB=3BC,点C对应的数为6,线段BC=4.
(1)直接写出点A对应的数为 ,点B对应的数为 ;
(2)动点P,Q同时从A,C两点出发,分别以每秒4个单位长度和每秒2个单位长度的速度沿数轴正
正半轴方向运动. M为AP中点,点N在CQ上,且CQ=3CN,设P,Q两点运动的时间为t秒.
①请用含t的代数式分别表示出点M和点N两点所对应的数;
②请问当t为何值时,OM=2BN?
综合探究三 线段的定值问题
3.在数轴上有A,B两点,点A对应的数为a,点B对应的数为b,且a,b满足|a+4|+(b-8)2=0.
(1)求线段AB的长;
(2)若点N从点A出发以3个单位长度/秒的速度向右运动,同时点M从B点出发以1个单位长度/秒
的速度向右运动;且D为MN的中点,E为DM的中点,若N在AB之间运动时,在DN之间始
终有一点Q使得EQ=3,试说明为定值.
综合探究四 角与单动线问题
4.已知∠AOB=120°(本题中的角均大于0°且小于180°)
(1)如图,在∠AOB内部作∠COD.若∠AOD+∠BOC=160°,求∠COD的度数;
(2)射线OI从OA的位置出发绕点O顺时针以每秒6°的速度旋转,旋转时间为t秒(0<t<30),射
线OM平分∠AOI,射线ON平分∠BOI,射线OP平分∠MON.若∠MOI=3∠POI,则t= 秒.
( http: / / www.21cnjy.com )
综合探究五 角与双动线问题
5.已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD(本题中的角均为大于0°且小于
180°的角)
(1)如图,当OB,OC重合时,求∠EOF的度数;
(2)当∠COD从图中所示位置绕点O顺时针旋转n°(0<n<40)时,∠AOE一∠BOF的值是否为定
值?若是定值,求出∠AOE-∠BOF的值;若不是,请说明理由.
( http: / / www.21cnjy.com )
综合探究六 角的定值问题
6.如图,两条直线AB,CD相交于点O,且∠AOC=∠AOD,射线OM从OB开始绕O点逆时针方向旋
转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s运动时间为t秒,(0<t<6,本题中的角均小于平角)21世纪教育网版权所有
(1)当t=2时,∠MON的度数为 ,∠BON的度数为 ;
(2)如图2,当射线OM在∠COB内部,是定值时,求t的取值范围,求这个定]
值.
( http: / / www.21cnjy.com )
21 七年级数学(上)第4章《几何图形初步》专题卷B——综合题探究(选用)
1.解:(1)a=-10,b=2;
(2)①当点D在B左侧时,设BD=x,则AC=2x,∴2x+x+n=12,得:x=4-,此时点D对应的数为2-(4-)=-2;21教育网
②当点D在B右侧时,设BD=x,则AC=2x,∴2x+n-x=12,得:x=12-n,此时点D对应的数为2+(12-n)=14-n.21cnjy.com
2.解:(1)点B对应的数为2,点A对应的数为-10;
(2)①运动t秒后,AP=4t,CQ=2t,∴AM=×4t=2t,点M在点A右侧,点M对应的数为21t-10;∵CN=×2t=t,点N在点C右侧,∴点N对应的数为t+6;21·cn·jy·com
②由①知,点M对应的数为(2t-10),N对应的数为(t+6),当t≤5时,OM=0-(2t-10)=10-2t,BN=(t+6)-2=t+4,由OM=2BN得,10-2t=2(t+4),解得t=;www.21-cn-jy.com
当t>5时,OM=2t-10,BN=t+6-2=t+4,由OM=2BN得,2t-10=2(t+4),解得t=27,综合上述,当t为秒或27秒时,OM=2BN.2·1·c·n·j·y
3.解:(1)a=-4,b=8,AB=12;
(2)设运动时间为t秒,运动t秒后点N对应的数为3t-4,点M对应的数为t+8,点D对应的数为2+2t,点E对应的t+5,N在AB间运动时,-4<3t-4<8,得0<t<4,∴-3t-4<2t+2<t+5<t+8,知点N,点D在点E的左侧,即点Q在点E的左侧,∴点Q对应的数为t+5-3=t+2,∴NQ=t+2-(3t-4)=6-t,NB=8-(3t-4)=12-3t,∴=,为定值.【来源:21·世纪·教育·网】
4.解:(1)∠COD=∠AOD+∠BOC-∠AOB=160°-120°=40°;
(2)7.5或15.设旋转n°,对于∠IOM,当0<n<180时,∠IOM=;当180<n<300时,∠IOM=180°-.对于∠POI,当0<n<60时,∠POI=30°-;当60<n<180时,∠POI=-30°.
分两种情况:①0<n<60,=(30-)×3,n=45,t=7.5;
②60<n<180,=(-30)×3,n=90,t=15.
5.解:(1)∠EOF=∠AOD=(∠AOB+∠COD)=70°;
(2)设∠AOE=∠COE=x,∠BO ( http: / / www.21cnjy.com )F=∠DOF=y°,∴∠BOC=2y-40°,∴∠AOB=∠AOC-∠BOC=2x-2y+40°=140°,x-y=30°,∴∠AOE-∠BOF=x-y=30°为定值.21·世纪*教育网
6.解:(1)144°;114°;
(2)当∠MON为平角时,t=,
①当0<t<时,∠COM=(90-15t)°,∠BON=(90+12t)°,∠MON=(90+15t+12t)°;∴==,不是定值;www-2-1-cnjy-com
②∵≤t<6,∠COM=(90-15t)°,∠BON=(90+12t)°,∠MON=(270-27t)°,2-1-c-n-j-y
∴==,=3,为定值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
