23.2.3关于原点对称的点的坐标 课件(共29张PPT)
文档属性
| 名称 | 23.2.3关于原点对称的点的坐标 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-06 20:49:38 | ||
图片预览


文档简介
(共29张PPT)
23.2.3 关于原点对称的点的坐标
人教版九年级上册
知识回顾
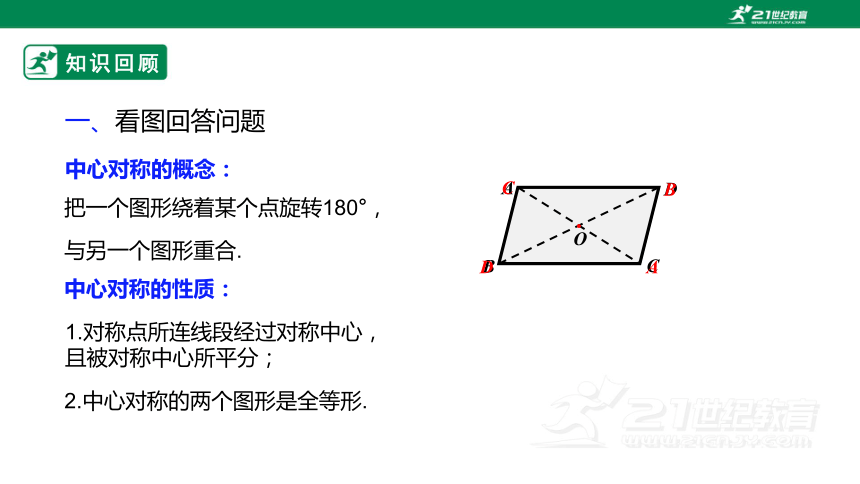
一、看图回答问题
中心对称的概念:
把一个图形绕着某个点旋转180°,
与另一个图形重合.
中心对称的性质:
1.对称点所连线段经过对称中心,
且被对称中心所平分;
2.中心对称的两个图形是全等形.
O
A
D
C
B
D
B
C
A
教学目标
1.掌握两点关于原点对称时,横纵坐标的关系.
2.会在平面直角坐标系内作关于原点对称的图形.
3.进一步体会数形结合的思想.
新知导入
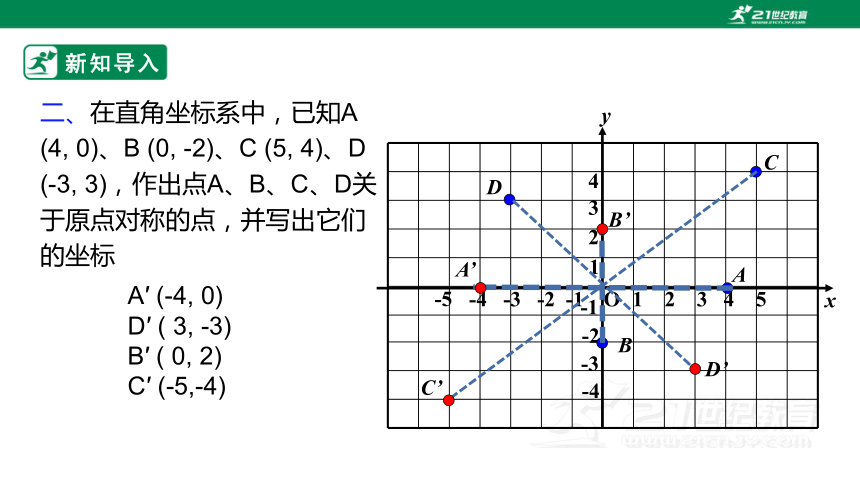
二、在直角坐标系中,已知A (4, 0)、B (0, -2)、C (5, 4)、D (-3, 3),作出点A、B、C、D关于原点对称的点,并写出它们的坐标
A′ (-4, 0)
D′ ( 3, -3)
B′ ( 0, 2)
C′ (-5,-4)
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
A
B
D
C
-5
-4
A’
B’
C’
D’
新知探究
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
(-4,0)
(-2,-1)
(1,-2)
-5
新知探究
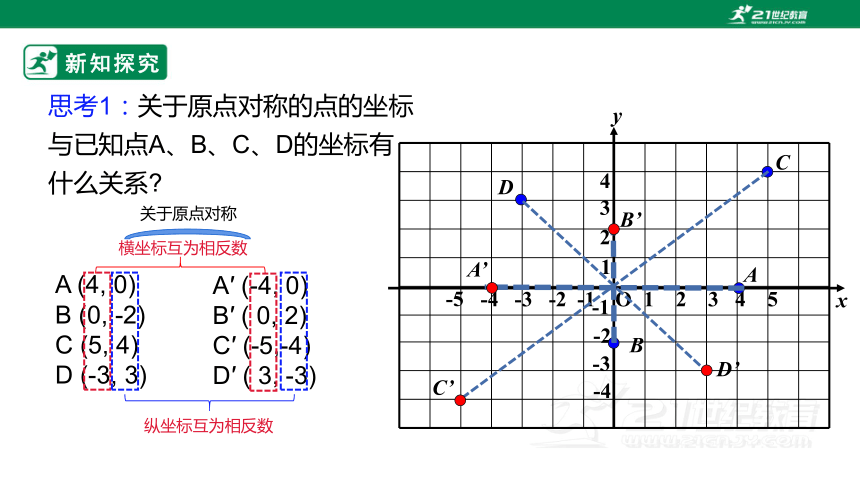
思考1:关于原点对称的点的坐标
与已知点A、B、C、D的坐标有
什么关系
关于原点对称
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
A
B
D
C
-5
-4
A’
B’
C’
D’
A′ (-4, 0)
B′ ( 0, 2)
C′ (-5,-4)
D′ ( 3, -3)
A (4, 0)
B (0, -2)
C (5, 4)
D (-3, 3)
横坐标互为相反数
纵坐标互为相反数
新知探究
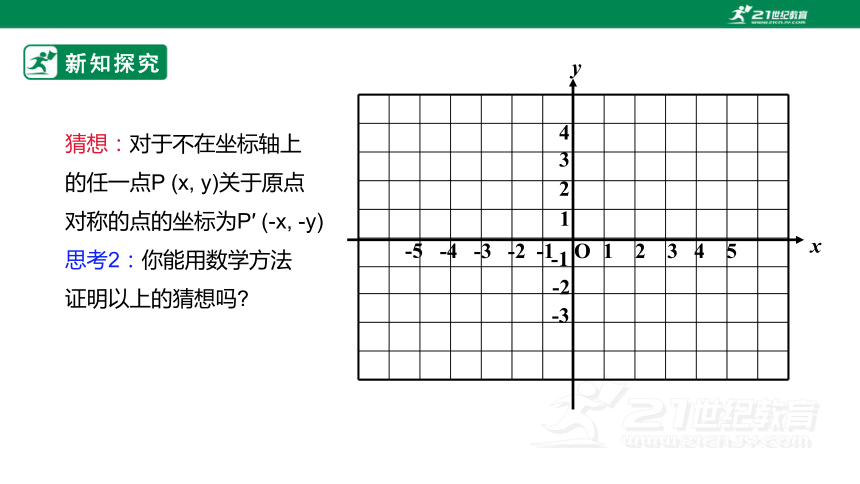
猜想:对于不在坐标轴上
的任一点P (x, y)关于原点
对称的点的坐标为P′ (-x, -y)
思考2:你能用数学方法
证明以上的猜想吗
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
-5
新知探究
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
-5
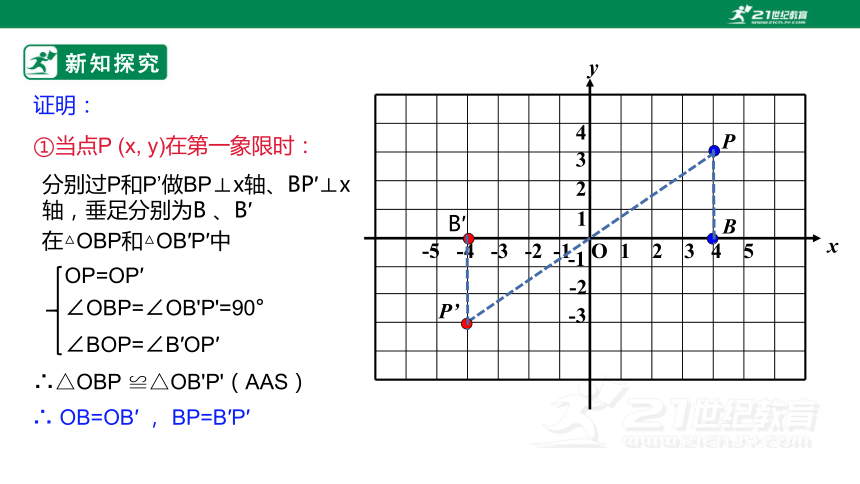
证明:
①当点P (x, y)在第一象限时:
在△OBP和△OB′P′中
OP=OP′
∠OBP=∠OB'P'=90°
∠BOP=∠B′OP′
∴△OBP ≌△OB'P'(AAS)
∴ OB=OB′ , BP=B′P′
P
P’
分别过P和P’做BP⊥x轴、BP′⊥x轴,垂足分别为B 、B′
B
B′
新知探究
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
-5
P
P’
B
B′
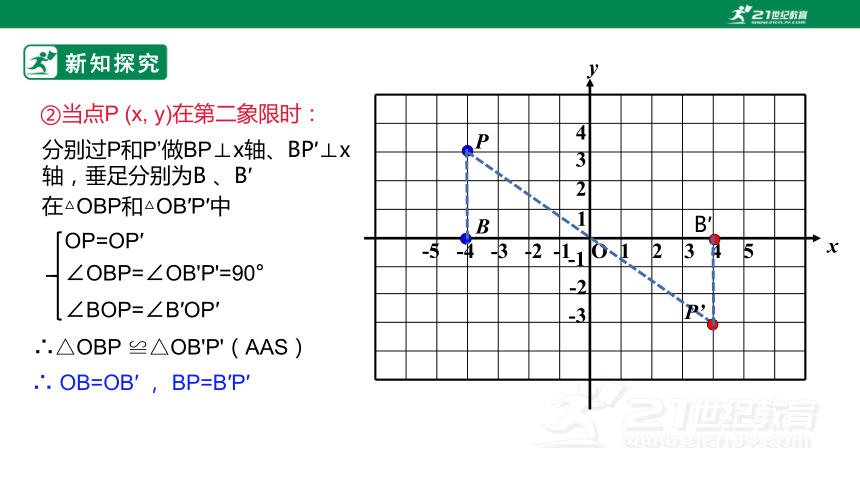
②当点P (x, y)在第二象限时:
在△OBP和△OB′P′中
OP=OP′
∠OBP=∠OB'P'=90°
∠BOP=∠B′OP′
∴△OBP ≌△OB'P'(AAS)
∴ OB=OB′ , BP=B′P′
分别过P和P’做BP⊥x轴、BP′⊥x轴,垂足分别为B 、B′
新知探究
由点P在第一象限和第二象限的情况可知,
点P在第三象限和第四象限时,OB=OB′ , BP=B′P′ 是否成立呢?
OB=OB′ , BP=B′P′ 依然成立
新知小结
当两点关于原点对称时,
1.两个点的横坐标的绝对值 ;两个点的纵坐标的绝对值 .
相 等
相 等
2.两个点的横坐标符号 ,纵坐标符号 .
相 反
相 反
新知小结
归纳总结:两个点关于原点对称时,他们的横坐标 ,纵坐标 ,即点P (x, y)关于原点对称的点的坐标是 .
互为相反数
当两点关于原点对称时,
互为相反数
P′ (-x, -y)
P′ (-x, -y)
新知练习
1.点A (2, 3) 关于原点对称的点的坐标是 ,
2. 点A (-4, 2) 关于原点对称的点的坐标是 ,
3. 点A (-3, a) 关于原点对称的点的坐标是 ,
4. 点A (m+1, n-3) 关于原点对称的点的坐标是 ,
5. 若A (m, -2) , B(1, n) 关于原点对称,则m = , n = .
(-2, -3)
(4, -2)
(3, -a)
(-m-1, -n+3)
-1
2
新知典例
例 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
A
C
B
A′
C′
B′
解:△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点分别为
依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的△ A′B′ C ′ .
新知小结
作关于原点对称的图形的步骤:
(1) 写出图形各顶点的坐标;
(2) 写出图形各顶点关于原点的对称点的坐标;
(3) 描点;
(4) 顺次连接;
(5) 下结论.
新知典例
例1
(1)在平面直角坐标系中,点P(7,-8)关于原点的对称点P′的坐标是 ;
(2)点P(2,n)与点Q(m,-3)关于原点对称,则(m+n)2 020= ;
(3)点M(5,-1)绕原点旋转180°后
到达的位置是 .
横纵坐标都变
m=-2
n=3
中心对称
(-7,8)
1
(-5,1)
新知探究
例2
四边形ABCD各顶点坐标分别为A(5,0),B(-2,3),C(-1,0),D(-1,-5),作出与四边形ABCD关于原点O对称的图形,并写出各点的对称点的坐标.
解:如图,四边形A′B′C′D′即为所求.点A,B,C,D的对称点的坐标分别为:A′(-5,0),B′(2,-3),C′(1,0),D′(1,5).
D′
C′
B′
A′
新知探究
例3
已知点M(2-a,b)与点N(-b-1,2)关于原点对称,求点M的坐标.
解:∵点M(2-a,b)与点N(-b-1,2)关于原点对称,
∴点M的坐标为(-1,-2).
解得:
新知练习
1.填空:
(1)点A (-3, 4) 关于原点的对称的点的坐标为 .
(2)点A (a, -2) 与点B (8, b)关于原点对称 a = ,b = .
(3)点A (2, 1) 与点B (2, -1) 关于 对称.
(4)点A (2, 1) 与点C (-2, -1) 关于 对称.
(5)点A (2, 1) 与点D (-2, 1) 关于 对称.
(3, -4)
-8
2
x 轴
原点
y 轴
新知练习
2.在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .
12
解:∵点 A 的坐标为(a,3),
点 B 的坐标是(4,b),
点 A 与点 B 关于原点 O 对称,
∴a=-4,b=-3,
则 ab=12.
新知练习
3.下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),E(0,5),F(-2,1),G(-2,-1).
解:点 C 与点 F 的横纵坐标分别互为相反数,
所以点 C 与点 F关于原点 O 对称.
新知练习
4.若点M(3,a-2),N(b,a)关于原点对称,则a + b= .
-2
解:由题意,得 b=-3,a-2+a=0,
解得 a=1,
∴a + b = -3 + 1 = -2.
新知练习
5.在平面直角坐标系中,第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,则x+2y= .
-7
解:根据题意,得 (x2+2x)+(x+2)=0,y=-3,
∴x1=-1,x2=-2(不符合题意,舍去).
∴x=-1,y=-3
∴x+2y=-7.
课堂总结
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作关于原点对称的图形,先求出对称点的坐标再描点画图.
课堂练习
2.若点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值是( )
A.33 B.-33 C.-7 D.7
D
3.已知点P(a-3,2b+4)与点Q(b+5,3a-7)关于原点对称,则直线y=ax+b经过 象限.
一、三、四
1.在平面直角坐标系中,点P(-3, -5)关于原点对称的点的坐标是( )
C
A. (3, -5) B.( -3,5) C. (3,5) D.( -3,-5)
课堂练习
4.在平面直角坐标系中,点P( 3,m +1)关于原点的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:点P关于原点对称的点的坐标为(3, (m +1)),
∵m +1 >0,
∴ ( m +1)<0,
故点P关于原点的对称点在第四象限.
D
课堂练习
5.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,- 300°)或P(3 ,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
D
Q(3,240°)
Q(3,- 120°)
C. Q(3,600°)
D. Q(3, -500°)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
23.2.3 关于原点对称的点的坐标
人教版九年级上册
知识回顾
一、看图回答问题
中心对称的概念:
把一个图形绕着某个点旋转180°,
与另一个图形重合.
中心对称的性质:
1.对称点所连线段经过对称中心,
且被对称中心所平分;
2.中心对称的两个图形是全等形.
O
A
D
C
B
D
B
C
A
教学目标
1.掌握两点关于原点对称时,横纵坐标的关系.
2.会在平面直角坐标系内作关于原点对称的图形.
3.进一步体会数形结合的思想.
新知导入
二、在直角坐标系中,已知A (4, 0)、B (0, -2)、C (5, 4)、D (-3, 3),作出点A、B、C、D关于原点对称的点,并写出它们的坐标
A′ (-4, 0)
D′ ( 3, -3)
B′ ( 0, 2)
C′ (-5,-4)
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
A
B
D
C
-5
-4
A’
B’
C’
D’
新知探究
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
(-4,0)
(-2,-1)
(1,-2)
-5
新知探究
思考1:关于原点对称的点的坐标
与已知点A、B、C、D的坐标有
什么关系
关于原点对称
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
A
B
D
C
-5
-4
A’
B’
C’
D’
A′ (-4, 0)
B′ ( 0, 2)
C′ (-5,-4)
D′ ( 3, -3)
A (4, 0)
B (0, -2)
C (5, 4)
D (-3, 3)
横坐标互为相反数
纵坐标互为相反数
新知探究
猜想:对于不在坐标轴上
的任一点P (x, y)关于原点
对称的点的坐标为P′ (-x, -y)
思考2:你能用数学方法
证明以上的猜想吗
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
-5
新知探究
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
-5
证明:
①当点P (x, y)在第一象限时:
在△OBP和△OB′P′中
OP=OP′
∠OBP=∠OB'P'=90°
∠BOP=∠B′OP′
∴△OBP ≌△OB'P'(AAS)
∴ OB=OB′ , BP=B′P′
P
P’
分别过P和P’做BP⊥x轴、BP′⊥x轴,垂足分别为B 、B′
B
B′
新知探究
x
y
O
-4 -3 -2 -1 1 2 3 4 5
-1
2
3
4
1
-2
-3
-5
P
P’
B
B′
②当点P (x, y)在第二象限时:
在△OBP和△OB′P′中
OP=OP′
∠OBP=∠OB'P'=90°
∠BOP=∠B′OP′
∴△OBP ≌△OB'P'(AAS)
∴ OB=OB′ , BP=B′P′
分别过P和P’做BP⊥x轴、BP′⊥x轴,垂足分别为B 、B′
新知探究
由点P在第一象限和第二象限的情况可知,
点P在第三象限和第四象限时,OB=OB′ , BP=B′P′ 是否成立呢?
OB=OB′ , BP=B′P′ 依然成立
新知小结
当两点关于原点对称时,
1.两个点的横坐标的绝对值 ;两个点的纵坐标的绝对值 .
相 等
相 等
2.两个点的横坐标符号 ,纵坐标符号 .
相 反
相 反
新知小结
归纳总结:两个点关于原点对称时,他们的横坐标 ,纵坐标 ,即点P (x, y)关于原点对称的点的坐标是 .
互为相反数
当两点关于原点对称时,
互为相反数
P′ (-x, -y)
P′ (-x, -y)
新知练习
1.点A (2, 3) 关于原点对称的点的坐标是 ,
2. 点A (-4, 2) 关于原点对称的点的坐标是 ,
3. 点A (-3, a) 关于原点对称的点的坐标是 ,
4. 点A (m+1, n-3) 关于原点对称的点的坐标是 ,
5. 若A (m, -2) , B(1, n) 关于原点对称,则m = , n = .
(-2, -3)
(4, -2)
(3, -a)
(-m-1, -n+3)
-1
2
新知典例
例 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
A
C
B
A′
C′
B′
解:△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点分别为
依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的△ A′B′ C ′ .
新知小结
作关于原点对称的图形的步骤:
(1) 写出图形各顶点的坐标;
(2) 写出图形各顶点关于原点的对称点的坐标;
(3) 描点;
(4) 顺次连接;
(5) 下结论.
新知典例
例1
(1)在平面直角坐标系中,点P(7,-8)关于原点的对称点P′的坐标是 ;
(2)点P(2,n)与点Q(m,-3)关于原点对称,则(m+n)2 020= ;
(3)点M(5,-1)绕原点旋转180°后
到达的位置是 .
横纵坐标都变
m=-2
n=3
中心对称
(-7,8)
1
(-5,1)
新知探究
例2
四边形ABCD各顶点坐标分别为A(5,0),B(-2,3),C(-1,0),D(-1,-5),作出与四边形ABCD关于原点O对称的图形,并写出各点的对称点的坐标.
解:如图,四边形A′B′C′D′即为所求.点A,B,C,D的对称点的坐标分别为:A′(-5,0),B′(2,-3),C′(1,0),D′(1,5).
D′
C′
B′
A′
新知探究
例3
已知点M(2-a,b)与点N(-b-1,2)关于原点对称,求点M的坐标.
解:∵点M(2-a,b)与点N(-b-1,2)关于原点对称,
∴点M的坐标为(-1,-2).
解得:
新知练习
1.填空:
(1)点A (-3, 4) 关于原点的对称的点的坐标为 .
(2)点A (a, -2) 与点B (8, b)关于原点对称 a = ,b = .
(3)点A (2, 1) 与点B (2, -1) 关于 对称.
(4)点A (2, 1) 与点C (-2, -1) 关于 对称.
(5)点A (2, 1) 与点D (-2, 1) 关于 对称.
(3, -4)
-8
2
x 轴
原点
y 轴
新知练习
2.在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .
12
解:∵点 A 的坐标为(a,3),
点 B 的坐标是(4,b),
点 A 与点 B 关于原点 O 对称,
∴a=-4,b=-3,
则 ab=12.
新知练习
3.下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),E(0,5),F(-2,1),G(-2,-1).
解:点 C 与点 F 的横纵坐标分别互为相反数,
所以点 C 与点 F关于原点 O 对称.
新知练习
4.若点M(3,a-2),N(b,a)关于原点对称,则a + b= .
-2
解:由题意,得 b=-3,a-2+a=0,
解得 a=1,
∴a + b = -3 + 1 = -2.
新知练习
5.在平面直角坐标系中,第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,则x+2y= .
-7
解:根据题意,得 (x2+2x)+(x+2)=0,y=-3,
∴x1=-1,x2=-2(不符合题意,舍去).
∴x=-1,y=-3
∴x+2y=-7.
课堂总结
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作关于原点对称的图形,先求出对称点的坐标再描点画图.
课堂练习
2.若点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值是( )
A.33 B.-33 C.-7 D.7
D
3.已知点P(a-3,2b+4)与点Q(b+5,3a-7)关于原点对称,则直线y=ax+b经过 象限.
一、三、四
1.在平面直角坐标系中,点P(-3, -5)关于原点对称的点的坐标是( )
C
A. (3, -5) B.( -3,5) C. (3,5) D.( -3,-5)
课堂练习
4.在平面直角坐标系中,点P( 3,m +1)关于原点的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:点P关于原点对称的点的坐标为(3, (m +1)),
∵m +1 >0,
∴ ( m +1)<0,
故点P关于原点的对称点在第四象限.
D
课堂练习
5.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,- 300°)或P(3 ,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
D
Q(3,240°)
Q(3,- 120°)
C. Q(3,600°)
D. Q(3, -500°)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
