2023-2024学年人教版八年级数学上册 11.2.1三角形的内角同步练习 (含答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册 11.2.1三角形的内角同步练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 347.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 21:06:18 | ||
图片预览

文档简介
11.2.1三角形的内角 同步练习
一、单选题
1.已知△ABC中,∠A=70°,∠B=60°,则∠C =( ).
A.50° B.60° C.70° D.80°
2.如图,,于点,则图中互余的角有( )对.
A.3 B.4 C.5 D.6
3.如图,AB//CD,,则与一定满足的关系是( )
A. B. C. D.
4.一个三角形三个内角的度数之比为,这个三角形一定是( )
A.直角三角形 B.等腰三角形 C.钝角三角形 D.锐角三角形
5.如果,在△ABC中,,,是边上的高,是的平分线,则的度数为( )
A.8° B.10° C.12° D.14°
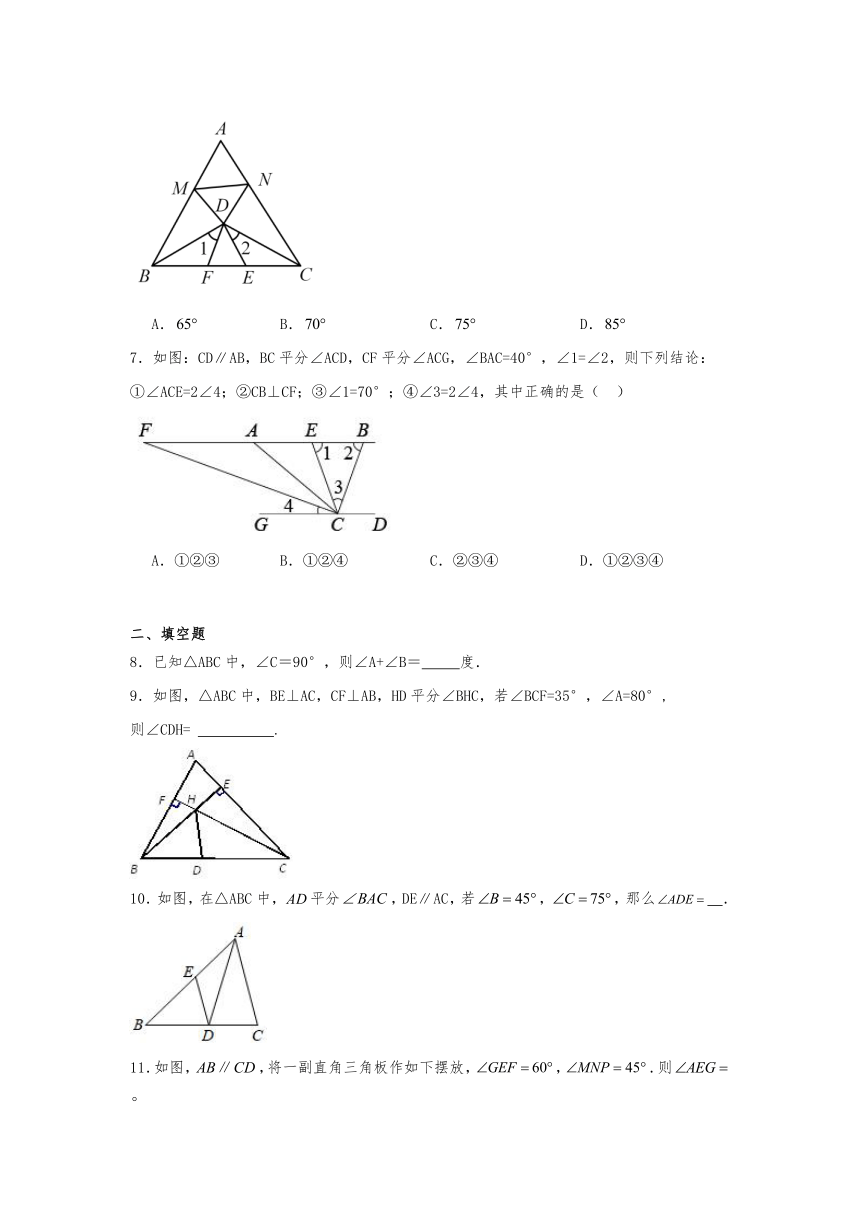
6.如图,、是△ABC边、上的点,△AMN沿翻折后得到△DMN,△BMD沿翻折后得到△BED,且点在边上,沿翻折后得到,且点在边上,若,则( )
A. B. C. D.
7.如图:CDAB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
8.已知△ABC中,∠C=90°,则∠A+∠B= 度.
9.如图,△ABC中,BE⊥AC,CF⊥AB,HD平分∠BHC,若∠BCF=35°,∠A=80°,
则∠CDH= .
10.如图,在△ABC中,平分,DEAC,若,,那么 .
11.如图,,将一副直角三角板作如下摆放,,.则
三、解答题
12.如图,平分,,求的度数.
请将下面的解答过程补充完整.
解:∵(已知)
∴在中,______________°( )
∵平分,∴__________=____________°( )
∵,∴____________=__________°( )
13.已知:如图,在△ABC中,,,点D,E分别在AB和AC上,且.求证:.
14.如图,△ABC中,是角平分线,且,,求的度数.
15.如图①,将△ABC纸片沿DE折叠,使点A落F的位置,DF与BC交于点G,EF与BC交于点M,∠A=80°,求∠1+∠2的度数;
参考答案
1.A
2.B
3.C
4.C
5.A
6.D
7.C
8.90.
9.95°
10.30°/30度
11.45
12.解:∵∠B=60°,∠A=70°,
∴在△ABC中,
∠ACB=180°-∠B-∠A=50°(三角形的内角和等于180°),
∵CD平分∠ACB,
∴∠DCB=∠ACB=25°(角平分线的定义),
∵DE∥BC,
∴∠EDC=∠DCB=25°(两直线平行,内错角相等).
13.在△ABC中,
∵, (已知),
∴(三角形内角和定理).
又∵(已知),
∴(两直线平行,同位角相等).
∴(等量代换).
14.25°
15.160°
一、单选题
1.已知△ABC中,∠A=70°,∠B=60°,则∠C =( ).
A.50° B.60° C.70° D.80°
2.如图,,于点,则图中互余的角有( )对.
A.3 B.4 C.5 D.6
3.如图,AB//CD,,则与一定满足的关系是( )
A. B. C. D.
4.一个三角形三个内角的度数之比为,这个三角形一定是( )
A.直角三角形 B.等腰三角形 C.钝角三角形 D.锐角三角形
5.如果,在△ABC中,,,是边上的高,是的平分线,则的度数为( )
A.8° B.10° C.12° D.14°
6.如图,、是△ABC边、上的点,△AMN沿翻折后得到△DMN,△BMD沿翻折后得到△BED,且点在边上,沿翻折后得到,且点在边上,若,则( )
A. B. C. D.
7.如图:CDAB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
8.已知△ABC中,∠C=90°,则∠A+∠B= 度.
9.如图,△ABC中,BE⊥AC,CF⊥AB,HD平分∠BHC,若∠BCF=35°,∠A=80°,
则∠CDH= .
10.如图,在△ABC中,平分,DEAC,若,,那么 .
11.如图,,将一副直角三角板作如下摆放,,.则
三、解答题
12.如图,平分,,求的度数.
请将下面的解答过程补充完整.
解:∵(已知)
∴在中,______________°( )
∵平分,∴__________=____________°( )
∵,∴____________=__________°( )
13.已知:如图,在△ABC中,,,点D,E分别在AB和AC上,且.求证:.
14.如图,△ABC中,是角平分线,且,,求的度数.
15.如图①,将△ABC纸片沿DE折叠,使点A落F的位置,DF与BC交于点G,EF与BC交于点M,∠A=80°,求∠1+∠2的度数;
参考答案
1.A
2.B
3.C
4.C
5.A
6.D
7.C
8.90.
9.95°
10.30°/30度
11.45
12.解:∵∠B=60°,∠A=70°,
∴在△ABC中,
∠ACB=180°-∠B-∠A=50°(三角形的内角和等于180°),
∵CD平分∠ACB,
∴∠DCB=∠ACB=25°(角平分线的定义),
∵DE∥BC,
∴∠EDC=∠DCB=25°(两直线平行,内错角相等).
13.在△ABC中,
∵, (已知),
∴(三角形内角和定理).
又∵(已知),
∴(两直线平行,同位角相等).
∴(等量代换).
14.25°
15.160°
