第十二章 全等三角形 复习学案(无答案) 2022—2023学年人教版八年级数学上册
文档属性
| 名称 | 第十二章 全等三角形 复习学案(无答案) 2022—2023学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 75.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 21:28:27 | ||
图片预览

文档简介
第十二章 全等三角形
一、概念:
全等形:能够完全重合的图形叫做全等形.
全等三角形:能够完全重合的两个三角形叫做全等三角形.
对应顶点、对应边、对应角:把两个全等的三角形重合到一起.重合的顶点叫做对应顶点;重合的边叫做对应边;重合的角叫做对应角.
二、全等三角形的性质:全等三角形的对应边相等、对应角相等.
三、三角形全等的条件:
1. 三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”).
2. 两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
3. 两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
4. 两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
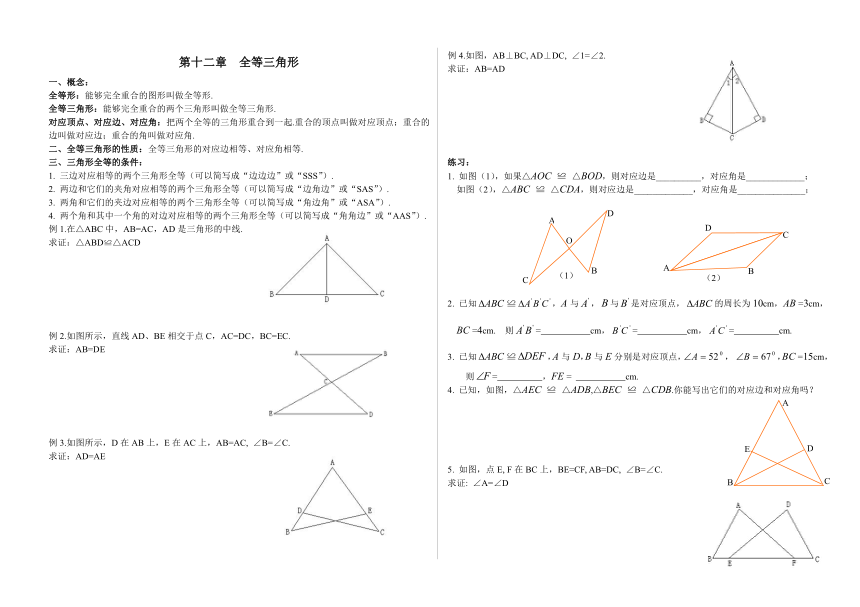
例1.在△ABC中,AB=AC,AD是三角形的中线.
求证:△ABD≌△ACD
例2.如图所示,直线AD、BE相交于点C,AC=DC,BC=EC.
求证:AB=DE
例3.如图所示,D在AB上,E在AC上,AB=AC, ∠B=∠C.
求证:AD=AE
例4.如图,AB⊥BC, AD⊥DC, ∠1=∠2.
求证:AB=AD
练习:
1. 如图(1),如果△AOC ≌ △BOD,则对应边是__________,对应角是_____________;
(
C
O
B
D
A
D
C
B
A
(
2
)
(
1
)
)如图(2),△ABC ≌ △CDA,则对应边是_____________,对应角是_______________;
2. 已知≌,A与,与是对应顶点,的周长为10cm,AB =3cm,BC =4cm. 则= cm,= cm,= cm.
3. 已知≌,A与D,B与E分别是对应顶点,, ,BC =15cm,则= ,FE = cm.
4. 已知,如图,△AEC ≌ △ADB,△BEC ≌ △CDB.你能写出它们的对应边和对应角吗?
(
D
C
E
B
A
)
5. 如图,点E, F在BC上,BE=CF, AB=DC, ∠B=∠C.
求证: ∠A=∠D
6. 如图,△ABC ≌ ,和是对应角,AB = AD是对应边,写出另外两组对应边和对应角.
(
B
△
AB
C
≌
D
△
AB
C
≌
C
△
AB
C
≌
E
△
AB
C
≌
A
△
AB
C
≌
)
(
A
△
AB
C
≌
) (
C
△
AB
C
≌
B
△
AB
C
≌
)7. 如图,△ABC ≌ △A′B′C′,∠C =25°,BC =6cm, AC =4cm, 你能得出△A′B′C′中哪些角的大小、哪些边的长度?
8. 如图,△ABD ≌ △EBD, △DBE ≌ △DCE, B, E, C在一条直线上.
BD是∠ABE的平分线吗?为什么?
(
B
C
E
D
A
)DE⊥BC吗?为什么?
点E 平分线段BC吗?为什么?
9. 将一几何图形放在平面镜前,则该图形与镜子里的图形全等,因为它们的______________相同
10. 如图,AB =CD,AD =BC,O为BD上任意一点,过O点的直线分别交AD,BC于M、N点.
(
A
B
C
D
M
N
O
1
2
)求证:
11. 如图在和中,点A,E,F,C在同一条直线上有下面四个论断:
(1)AD =CB , (2)AE =CF , (3), (4)AD //BC .
请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程.
(
A
E
B
C
F
D
)
12. 填空题:
(1)如图1,已知:AC =DB,要使≌,只需增加一个条件是_____ ____.
(2)如图2,已知:中,,AM平分,CM =20cm那么M到AB的距离
是 .
(3)如图3,已知:在和中,如果AB =DE,BC =EF,只要找出 = 或 =
(
A
B
D
F
E
C
图
3
) (
A
B
O
D
C
图
1
)或 // ,就可证得≌.
(
A
C
B
M
图
2
)
(4). 已知:如图4,AB =EB,∠1=∠2,∠ADE =120°,AE、BD相交于F,则∠3的度数为___ ___.
(5). 如图5, 已知:∠1 =∠2 , ∠3 =∠4 , 要证BD =CD , 需先证△AEB ≌△A EC , 根据是_________再证△BDE ≌△__ ____ , 根据是__ ________.
(
A
B
D
F
E
1
2
3
4
2
1
E
D
C
B
A
3
4
D
C
B
A
E
图
5
图
6
图
4
)(6). 已知:如图6 , ACBC于C , DEAC于E , ADAB于A , BC =AE.若AB = 5 , 则AD =___________.
一、概念:
全等形:能够完全重合的图形叫做全等形.
全等三角形:能够完全重合的两个三角形叫做全等三角形.
对应顶点、对应边、对应角:把两个全等的三角形重合到一起.重合的顶点叫做对应顶点;重合的边叫做对应边;重合的角叫做对应角.
二、全等三角形的性质:全等三角形的对应边相等、对应角相等.
三、三角形全等的条件:
1. 三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”).
2. 两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
3. 两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
4. 两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
例1.在△ABC中,AB=AC,AD是三角形的中线.
求证:△ABD≌△ACD
例2.如图所示,直线AD、BE相交于点C,AC=DC,BC=EC.
求证:AB=DE
例3.如图所示,D在AB上,E在AC上,AB=AC, ∠B=∠C.
求证:AD=AE
例4.如图,AB⊥BC, AD⊥DC, ∠1=∠2.
求证:AB=AD
练习:
1. 如图(1),如果△AOC ≌ △BOD,则对应边是__________,对应角是_____________;
(
C
O
B
D
A
D
C
B
A
(
2
)
(
1
)
)如图(2),△ABC ≌ △CDA,则对应边是_____________,对应角是_______________;
2. 已知≌,A与,与是对应顶点,的周长为10cm,AB =3cm,BC =4cm. 则= cm,= cm,= cm.
3. 已知≌,A与D,B与E分别是对应顶点,, ,BC =15cm,则= ,FE = cm.
4. 已知,如图,△AEC ≌ △ADB,△BEC ≌ △CDB.你能写出它们的对应边和对应角吗?
(
D
C
E
B
A
)
5. 如图,点E, F在BC上,BE=CF, AB=DC, ∠B=∠C.
求证: ∠A=∠D
6. 如图,△ABC ≌ ,和是对应角,AB = AD是对应边,写出另外两组对应边和对应角.
(
B
△
AB
C
≌
D
△
AB
C
≌
C
△
AB
C
≌
E
△
AB
C
≌
A
△
AB
C
≌
)
(
A
△
AB
C
≌
) (
C
△
AB
C
≌
B
△
AB
C
≌
)7. 如图,△ABC ≌ △A′B′C′,∠C =25°,BC =6cm, AC =4cm, 你能得出△A′B′C′中哪些角的大小、哪些边的长度?
8. 如图,△ABD ≌ △EBD, △DBE ≌ △DCE, B, E, C在一条直线上.
BD是∠ABE的平分线吗?为什么?
(
B
C
E
D
A
)DE⊥BC吗?为什么?
点E 平分线段BC吗?为什么?
9. 将一几何图形放在平面镜前,则该图形与镜子里的图形全等,因为它们的______________相同
10. 如图,AB =CD,AD =BC,O为BD上任意一点,过O点的直线分别交AD,BC于M、N点.
(
A
B
C
D
M
N
O
1
2
)求证:
11. 如图在和中,点A,E,F,C在同一条直线上有下面四个论断:
(1)AD =CB , (2)AE =CF , (3), (4)AD //BC .
请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程.
(
A
E
B
C
F
D
)
12. 填空题:
(1)如图1,已知:AC =DB,要使≌,只需增加一个条件是_____ ____.
(2)如图2,已知:中,,AM平分,CM =20cm那么M到AB的距离
是 .
(3)如图3,已知:在和中,如果AB =DE,BC =EF,只要找出 = 或 =
(
A
B
D
F
E
C
图
3
) (
A
B
O
D
C
图
1
)或 // ,就可证得≌.
(
A
C
B
M
图
2
)
(4). 已知:如图4,AB =EB,∠1=∠2,∠ADE =120°,AE、BD相交于F,则∠3的度数为___ ___.
(5). 如图5, 已知:∠1 =∠2 , ∠3 =∠4 , 要证BD =CD , 需先证△AEB ≌△A EC , 根据是_________再证△BDE ≌△__ ____ , 根据是__ ________.
(
A
B
D
F
E
1
2
3
4
2
1
E
D
C
B
A
3
4
D
C
B
A
E
图
5
图
6
图
4
)(6). 已知:如图6 , ACBC于C , DEAC于E , ADAB于A , BC =AE.若AB = 5 , 则AD =___________.
