4.5 一元一次不等式组 课件(共19张PPT)
文档属性
| 名称 | 4.5 一元一次不等式组 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 09:16:39 | ||
图片预览






文档简介
(共19张PPT)
8.4 一元一次不等式组
1.经历通过具体问题抽象出不等式组的过程;
2.理解一元一次不等式组及其解的意义,初步感知用数轴确定不等式组的解集.
3.掌握解一元一次不等式组的基本步骤,能应用其解决简单的实际问题.
某社区今年冬季烧煤时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨,该校计划每月烧煤多少吨?
【解析】设计划每月烧煤x吨,根据题意,得
【定义】由几个含有同一个未知数x的一元一次不等式所组成的不等式组,叫做一元一次不等式组.
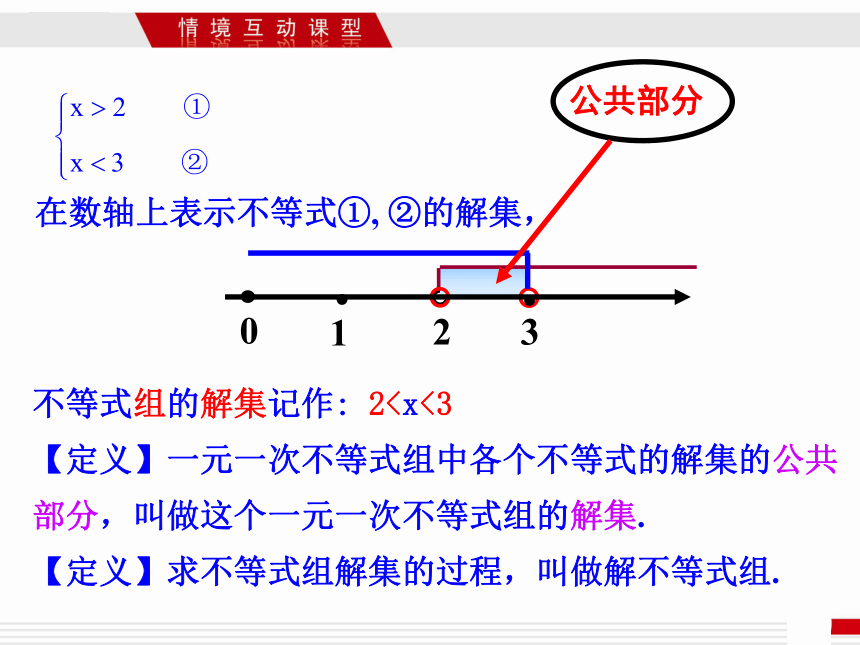
一元一次不等式x>2与x<3合在一起,就组成了一元一次不等式组,记作
【分析】
在数轴上表示不等式①, ②的解集,
不等式组的解集记作: 2【定义】一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
【定义】求不等式组解集的过程,叫做解不等式组.
公共部分
2
3
0
1
【归纳升华】
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
不等式组无解
a b
a b
–2 –1 0 1 2
–2 –1 0 1 2
【做一做】
不等式组的解集在数轴上表示如图,其解集是什么?
不等式组无解
–2 –1 0 1 2
-3
-2
-1
0
4
2
1
3
5
例1 解不等式组
【解析】解不等式①,得x>-1.
解不等式②,得x<3.
在数轴上表示不等式①, ②的解集
所以这个不等式组的解集是-1-1
3
0
【例题】
例2 解不等式组:
【解析】解不等式①,得x>2.5
解不等式②,得x≥4.
在同一条数轴上表示不等式①②的解集,
所以,原不等式组的解集为x≥4.
【议一议】
是否存在实数x,使得x+3<5,且x-2>4
【解析】解不等式组 无解.
【结论】
并不是所有的不等式组都有解.
例3 甲以5 km/h的速度进行有氧体育锻炼,2h后,乙骑自行车从同地出发沿同一条路追赶甲.根据他们两人的约定,乙最快不早于1h追上甲,最慢不晚于1h 15min追上甲.乙骑车的速度应当控制在什么范围内?
【解析】设乙骑车的速度为 x km/h,1h 15min =1.25h,
根据题意,得:
解得13≤x≤15.因此,乙骑车的速度应控制在13km/h到15km/h这个范围.
1.(宁夏·中考)若关于x的不等式组
的解集是x>2,则m的取值范围是______.
【解析】根据“大大取大”可知m≤2.
答案:m≤2
2.(台州·中考)解不等式组 并把解集在数轴上表示出来.
【解析】解①得x<3,解②得x>1,
∴不等式组的解集是1<x<3.
在数轴上表示:
3.某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品,需用甲种原料9千克,乙种原料3千克,可获利700元.生产一件B产品需用甲种原料4千克,乙种原料10千克,获利1 200元.
(1)按要求安排A,B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A,B两种产品获总利润y元,其中一种的生产件数为x,试写出y与x之间的关系,并利用相关的性质说明(1)中哪种生产方案获总利润最大?最大利润是多少?
【解析】(1)设安排生产A种产品x件,则生产B种产品(50-x)
件,由题意得
解得:30≤x≤32
因为x取整数,所以x=30或x=31或x=32;
故生产方案有三种:A 30件,B 20件;A 31件,B 19件; A 32件,B 18件.
(2)设生产A产品x件,则生产B产品(50-x)件,
由题意得:y=700x+1 200(50-x)=-500x+60 000.
所以当x=30时,获得利润最大,最大利润为45 000元.
通过本课时的学习,需要我们掌握:
1.有关不等式组的定义及解一元一次不等式组的基本方法和步骤.
2.列一元一次不等式组解决实际问题的一般步骤:审、找、列、解、答.其中审题、找不等关系式是关键.
含泪播种的人一定能含笑收获。
8.4 一元一次不等式组
1.经历通过具体问题抽象出不等式组的过程;
2.理解一元一次不等式组及其解的意义,初步感知用数轴确定不等式组的解集.
3.掌握解一元一次不等式组的基本步骤,能应用其解决简单的实际问题.
某社区今年冬季烧煤时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨,该校计划每月烧煤多少吨?
【解析】设计划每月烧煤x吨,根据题意,得
【定义】由几个含有同一个未知数x的一元一次不等式所组成的不等式组,叫做一元一次不等式组.
一元一次不等式x>2与x<3合在一起,就组成了一元一次不等式组,记作
【分析】
在数轴上表示不等式①, ②的解集,
不等式组的解集记作: 2
【定义】求不等式组解集的过程,叫做解不等式组.
公共部分
2
3
0
1
【归纳升华】
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
不等式组无解
a b
a b
–2 –1 0 1 2
–2 –1 0 1 2
【做一做】
不等式组的解集在数轴上表示如图,其解集是什么?
不等式组无解
–2 –1 0 1 2
-3
-2
-1
0
4
2
1
3
5
例1 解不等式组
【解析】解不等式①,得x>-1.
解不等式②,得x<3.
在数轴上表示不等式①, ②的解集
所以这个不等式组的解集是-1
3
0
【例题】
例2 解不等式组:
【解析】解不等式①,得x>2.5
解不等式②,得x≥4.
在同一条数轴上表示不等式①②的解集,
所以,原不等式组的解集为x≥4.
【议一议】
是否存在实数x,使得x+3<5,且x-2>4
【解析】解不等式组 无解.
【结论】
并不是所有的不等式组都有解.
例3 甲以5 km/h的速度进行有氧体育锻炼,2h后,乙骑自行车从同地出发沿同一条路追赶甲.根据他们两人的约定,乙最快不早于1h追上甲,最慢不晚于1h 15min追上甲.乙骑车的速度应当控制在什么范围内?
【解析】设乙骑车的速度为 x km/h,1h 15min =1.25h,
根据题意,得:
解得13≤x≤15.因此,乙骑车的速度应控制在13km/h到15km/h这个范围.
1.(宁夏·中考)若关于x的不等式组
的解集是x>2,则m的取值范围是______.
【解析】根据“大大取大”可知m≤2.
答案:m≤2
2.(台州·中考)解不等式组 并把解集在数轴上表示出来.
【解析】解①得x<3,解②得x>1,
∴不等式组的解集是1<x<3.
在数轴上表示:
3.某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品,需用甲种原料9千克,乙种原料3千克,可获利700元.生产一件B产品需用甲种原料4千克,乙种原料10千克,获利1 200元.
(1)按要求安排A,B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A,B两种产品获总利润y元,其中一种的生产件数为x,试写出y与x之间的关系,并利用相关的性质说明(1)中哪种生产方案获总利润最大?最大利润是多少?
【解析】(1)设安排生产A种产品x件,则生产B种产品(50-x)
件,由题意得
解得:30≤x≤32
因为x取整数,所以x=30或x=31或x=32;
故生产方案有三种:A 30件,B 20件;A 31件,B 19件; A 32件,B 18件.
(2)设生产A产品x件,则生产B产品(50-x)件,
由题意得:y=700x+1 200(50-x)=-500x+60 000.
所以当x=30时,获得利润最大,最大利润为45 000元.
通过本课时的学习,需要我们掌握:
1.有关不等式组的定义及解一元一次不等式组的基本方法和步骤.
2.列一元一次不等式组解决实际问题的一般步骤:审、找、列、解、答.其中审题、找不等关系式是关键.
含泪播种的人一定能含笑收获。
同课章节目录
