4.1 空间图形基本关系的认识 4.2 空间图形的公理(公理1,2,3)
文档属性
| 名称 | 4.1 空间图形基本关系的认识 4.2 空间图形的公理(公理1,2,3) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 08:36:59 | ||
图片预览






文档简介
课件29张PPT。§4 空间图形的基本关系与公理
4.1 空间图形基本关系的认识
4.2 空间图形的公理(公理1,2,3)空间图形是丰富的,它由一些基本的图形:点、线、面组成,认识清楚它们的位置关系,对于我们认识空间图形是很重要的,今天我们就来学习这些关系!1.通过长方体这一常见的空间图形,了解空间图形的基本构成----点、线、面的基本位置关系.(难点)
2.掌握空间图形的三个基本公理.(重点)
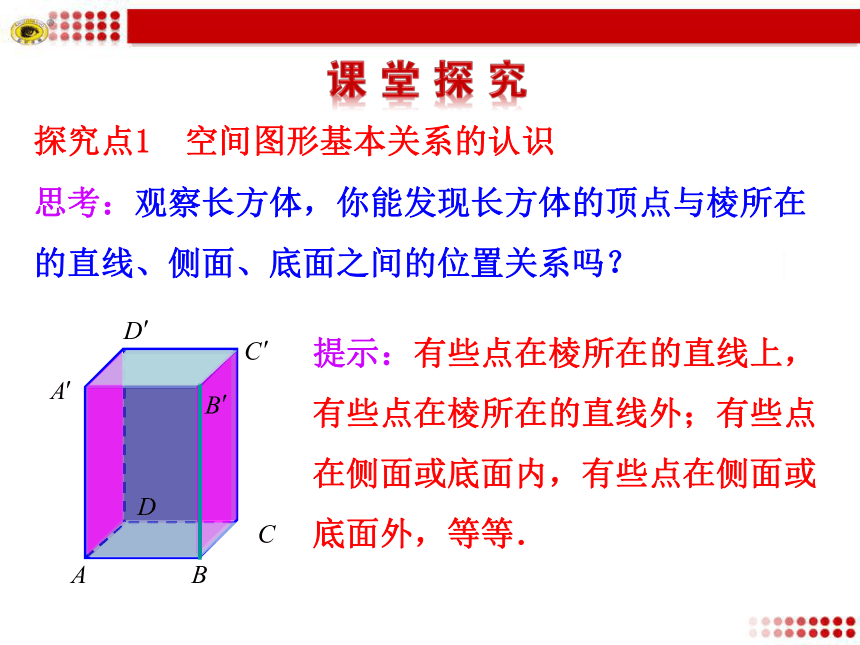
3.培养空间想象能力及运用图形语言进行交流的能力.思考:观察长方体,你能发现长方体的顶点与棱所在的直线、侧面、底面之间的位置关系吗?提示:有些点在棱所在的直线上,有些点在棱所在的直线外;有些点在侧面或底面内,有些点在侧面或底面外,等等.探究点1 空间图形基本关系的认识问题1:观察上述长方体,并填空 .
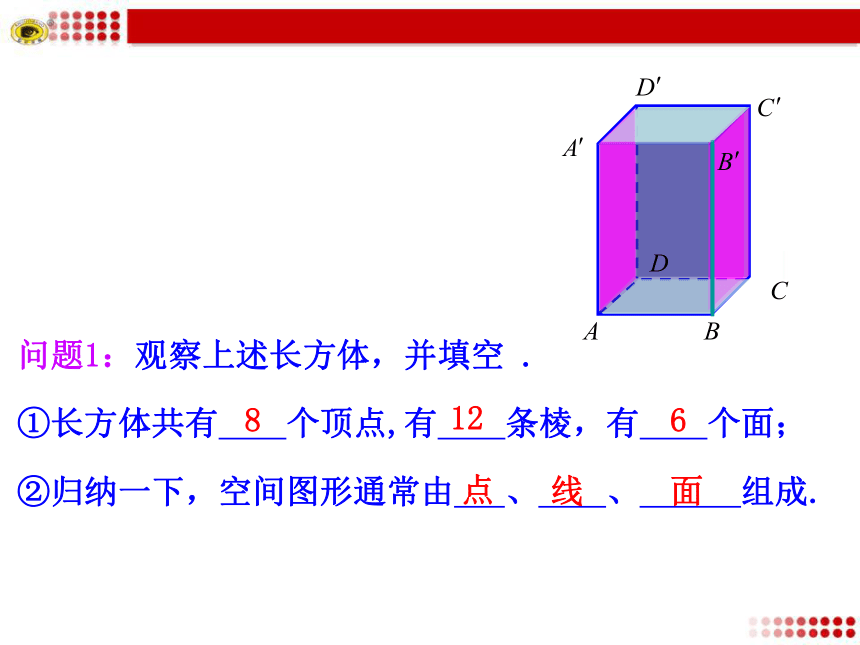
①长方体共有 个顶点,有 条棱,有 个面;
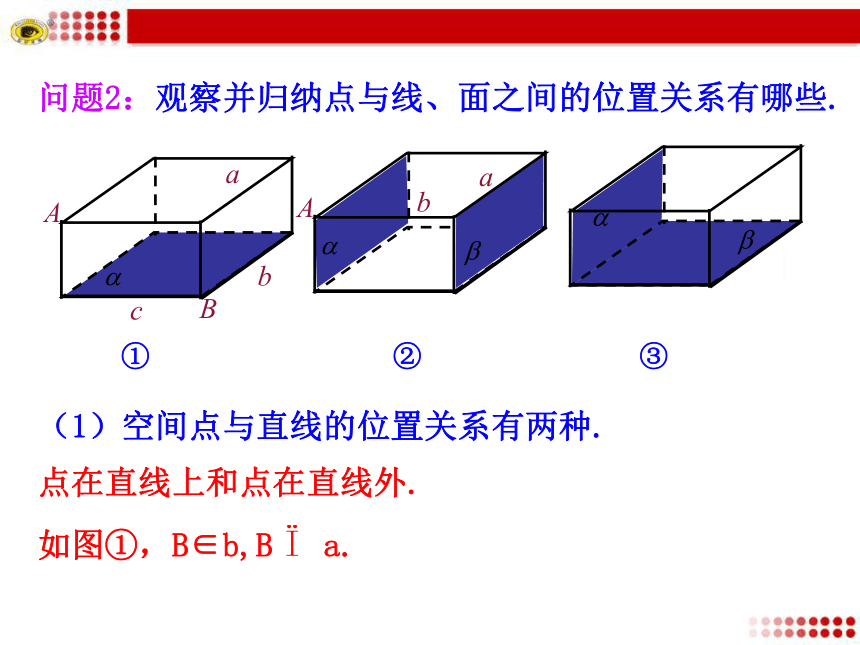
②归纳一下,空间图形通常由 、 、 组成.86面点线12问题2:观察并归纳点与线、面之间的位置关系有哪些. abA(1)空间点与直线的位置关系有两种.点在直线上和点在直线外. ②①③如图①,B∈b,B a.(2)空间点与平面的位置关系有两种:点在平面内和点在平面外. 如图①,思考交流
1. 观察图①②③所示的长方体,再举出一些点、线、面的位置关系的例子.2. 观察你周围的一些实物,指出一些点、线、面的位置关系.用三角架支撑照相机.思考1:我们知道,两点确定一条直线.那么怎样确定一个平面呢?探究点2:空间图形的公理测量员用三角架支撑测量仪器平板仪.公理1 过不在一条直线上的三点,有且只有一个平面(即可以确定一个平面).ACB经过不在同一条直线上的三个点A,B,C
的平面α,又可记作“平面ABC”.确定平面的主要依据.思考2:(1)一条直线和直线外一点,可以确定一个平面吗?
提示:可以.
(2)两条相交直线,可以确定一个平面吗?
提示:可以.
(3)两条平行直线,可以确定一个平面吗?
提示:可以.提升总结:三条结论
1. 一条直线和直线外一点确定一个平面.
2. 两条相交直线确定一个平面.
3. 两条平行直线确定一个平面.思考3:如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?提示:不一定.提示:实际生活中,我们有这样的经验:把一把直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.思考4:如果直线l与平面α有两个公共点,直线l是否在平面α内?在平面α内公理2 如果一条直线上的两点在一个平面内,那么这条直线在此平面内(即直线在平面内).ABl 公理是进一步推理的
基础.思考5:观察长方体,你发现长方体的两个平面有什么位置关系?提示:两个平面平行或者相交.平面与平面的公共直线叫作交线.思考6:把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?B提示:不只相交于一点B,如下图所示:公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.②判断点在直线上.lP1.下列说法中正确的是(???? )
A.经过三点确定一个平面????
B.两条直线确定一个平面
C.四边形确定一个平面?????
D.不共面的四点可以确定4个平面D2.下列命题中正确的是( )
A.空间三点可以确定一个平面
B.三角形一定是平面图形
C.若A,B,C,D既在平面α内,又在平面β内,
则平面α和平面β重合
D.四条边都相等的四边形是平面图形B【解析】选B.A、根据公理1知,必须是不共线的三点确定一个平面,故A不对;
B、因为三角形的3个顶点不共线,所以由公理1知一定确定一个平面,故B正确;
C、当A,B,C,D四点在两个平面的交线上时,满足是两个平面的交点,但是这两个平面相交,故C不对;
D、比如空间四边形则不是平面图形,故D不对. 故选B.3.下列图形中不一定是平面图形的是( )
A.三角形
B.梯形
C.对角线相交的四边形
D.边长相等的四边形D【解析】选D.由不共线的三点确定一个平面,知三角形是平面图形,故A一定是平面图形; 由两条平行线确定一个平面,知梯形是一个平面图形,故B一定是平面图形; 由两条相交直线确定一个平面,知对角线相交的四边形是平面图形,故C一定是平面图形; 边长相等的四边形有可能是平面图形,也有可能是空间四边形,故D不一定是平面图形. 故选D.①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形4.下列说法中,正确的是___②5.如图,用符号表示下列图形中点、直线、平面之间的位置关系.(2)解:在(1)中,在(2)中,实例引入空间图形的基本关系点、直线、平面的位置关系平面三个公理不能自助的人也难以受到别人的帮助.
4.1 空间图形基本关系的认识
4.2 空间图形的公理(公理1,2,3)空间图形是丰富的,它由一些基本的图形:点、线、面组成,认识清楚它们的位置关系,对于我们认识空间图形是很重要的,今天我们就来学习这些关系!1.通过长方体这一常见的空间图形,了解空间图形的基本构成----点、线、面的基本位置关系.(难点)
2.掌握空间图形的三个基本公理.(重点)
3.培养空间想象能力及运用图形语言进行交流的能力.思考:观察长方体,你能发现长方体的顶点与棱所在的直线、侧面、底面之间的位置关系吗?提示:有些点在棱所在的直线上,有些点在棱所在的直线外;有些点在侧面或底面内,有些点在侧面或底面外,等等.探究点1 空间图形基本关系的认识问题1:观察上述长方体,并填空 .
①长方体共有 个顶点,有 条棱,有 个面;
②归纳一下,空间图形通常由 、 、 组成.86面点线12问题2:观察并归纳点与线、面之间的位置关系有哪些. abA(1)空间点与直线的位置关系有两种.点在直线上和点在直线外. ②①③如图①,B∈b,B a.(2)空间点与平面的位置关系有两种:点在平面内和点在平面外. 如图①,思考交流
1. 观察图①②③所示的长方体,再举出一些点、线、面的位置关系的例子.2. 观察你周围的一些实物,指出一些点、线、面的位置关系.用三角架支撑照相机.思考1:我们知道,两点确定一条直线.那么怎样确定一个平面呢?探究点2:空间图形的公理测量员用三角架支撑测量仪器平板仪.公理1 过不在一条直线上的三点,有且只有一个平面(即可以确定一个平面).ACB经过不在同一条直线上的三个点A,B,C
的平面α,又可记作“平面ABC”.确定平面的主要依据.思考2:(1)一条直线和直线外一点,可以确定一个平面吗?
提示:可以.
(2)两条相交直线,可以确定一个平面吗?
提示:可以.
(3)两条平行直线,可以确定一个平面吗?
提示:可以.提升总结:三条结论
1. 一条直线和直线外一点确定一个平面.
2. 两条相交直线确定一个平面.
3. 两条平行直线确定一个平面.思考3:如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?提示:不一定.提示:实际生活中,我们有这样的经验:把一把直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.思考4:如果直线l与平面α有两个公共点,直线l是否在平面α内?在平面α内公理2 如果一条直线上的两点在一个平面内,那么这条直线在此平面内(即直线在平面内).ABl 公理是进一步推理的
基础.思考5:观察长方体,你发现长方体的两个平面有什么位置关系?提示:两个平面平行或者相交.平面与平面的公共直线叫作交线.思考6:把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?B提示:不只相交于一点B,如下图所示:公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.②判断点在直线上.lP1.下列说法中正确的是(???? )
A.经过三点确定一个平面????
B.两条直线确定一个平面
C.四边形确定一个平面?????
D.不共面的四点可以确定4个平面D2.下列命题中正确的是( )
A.空间三点可以确定一个平面
B.三角形一定是平面图形
C.若A,B,C,D既在平面α内,又在平面β内,
则平面α和平面β重合
D.四条边都相等的四边形是平面图形B【解析】选B.A、根据公理1知,必须是不共线的三点确定一个平面,故A不对;
B、因为三角形的3个顶点不共线,所以由公理1知一定确定一个平面,故B正确;
C、当A,B,C,D四点在两个平面的交线上时,满足是两个平面的交点,但是这两个平面相交,故C不对;
D、比如空间四边形则不是平面图形,故D不对. 故选B.3.下列图形中不一定是平面图形的是( )
A.三角形
B.梯形
C.对角线相交的四边形
D.边长相等的四边形D【解析】选D.由不共线的三点确定一个平面,知三角形是平面图形,故A一定是平面图形; 由两条平行线确定一个平面,知梯形是一个平面图形,故B一定是平面图形; 由两条相交直线确定一个平面,知对角线相交的四边形是平面图形,故C一定是平面图形; 边长相等的四边形有可能是平面图形,也有可能是空间四边形,故D不一定是平面图形. 故选D.①有三个公共点的两个平面重合
②梯形的四个顶点在同一个平面内
③三条互相平行的直线必共面
④ 四条线段顺次首尾连接,构成平面图形4.下列说法中,正确的是___②5.如图,用符号表示下列图形中点、直线、平面之间的位置关系.(2)解:在(1)中,在(2)中,实例引入空间图形的基本关系点、直线、平面的位置关系平面三个公理不能自助的人也难以受到别人的帮助.
同课章节目录
