4.2 空间图形的公理(公理4、定理)
文档属性
| 名称 | 4.2 空间图形的公理(公理4、定理) |  | |
| 格式 | zip | ||
| 文件大小 | 1009.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 08:37:14 | ||
图片预览



文档简介
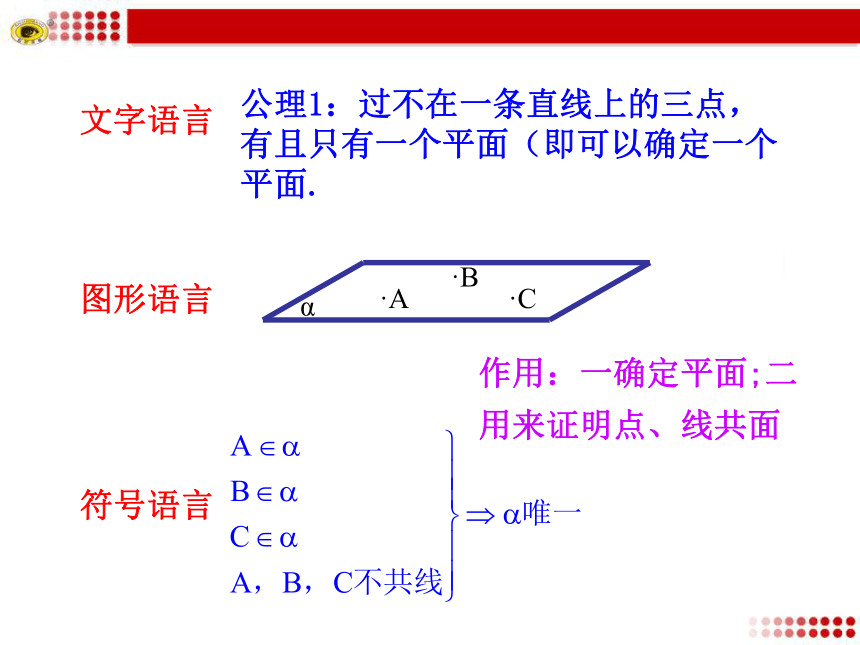
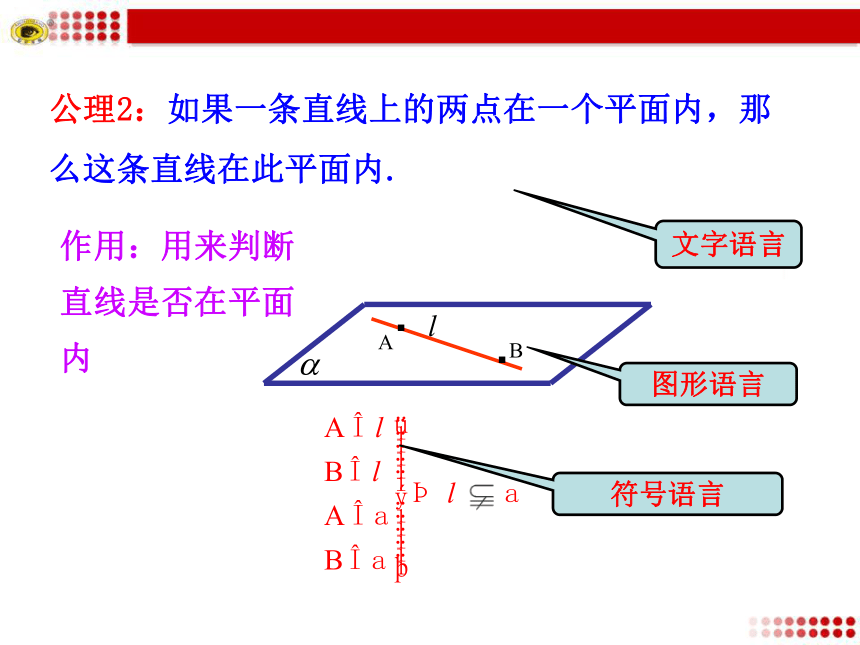
课件29张PPT。 4.2 空间图形的公理(公理4、定理) 空间图形多种多样,但它们的基本关系很容易观察到,一个小小的长方体,就包含了所有的基本关系. 上节课我们学习了哪几个公理,它们怎么表示,又有什么作用呢?文字语言图形语言符号语言公理1:过不在一条直线上的三点,有且只有一个平面(即可以确定一个平面.·A·B·C作用:一确定平面;二用来证明点、线共面作用:用来判断直线是否在平面内公理2:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.文字语言图形语言符号语言文字语言图形语言符号语言公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.αβ·P作用:一是判定两个平面是否相交;二是判断点在直线上.1.掌握公理4及“等角定理”. (重点)
2.能正确应用公理4判断空间两直线平行.(重点)
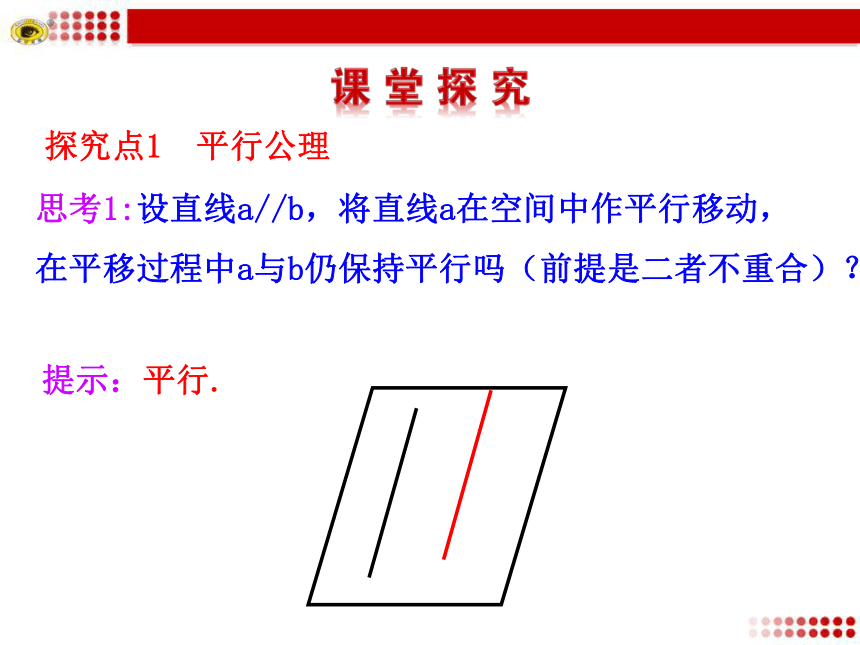
3.理解两异面直线的定义,会求两异面直线所成的角.(难点)思考1:设直线a//b,将直线a在空间中作平行移动,
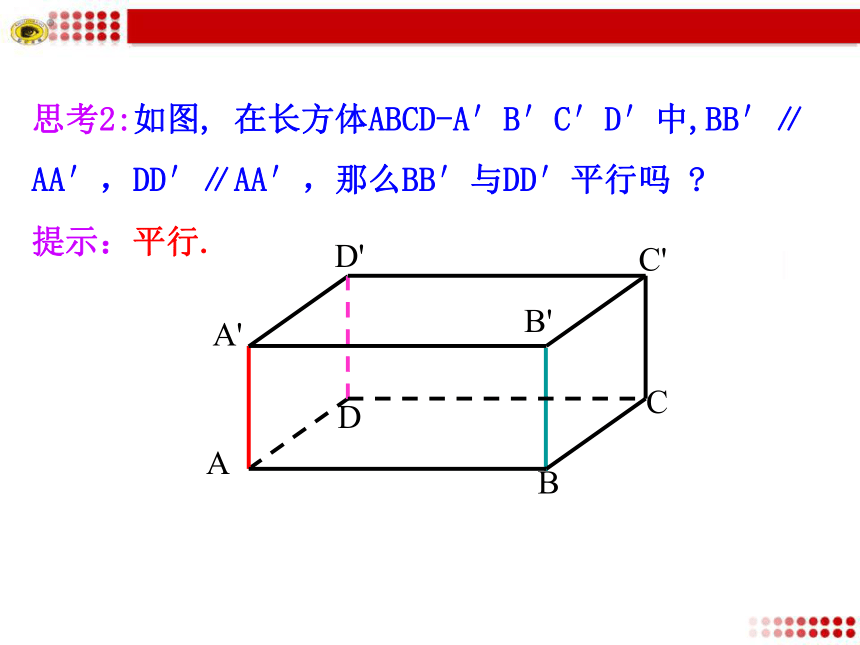
在平移过程中a与b仍保持平行吗(前提是二者不重合)?探究点1 平行公理提示:平行.思考2:如图, 在长方体ABCD-A′B′C′D′中,BB′∥
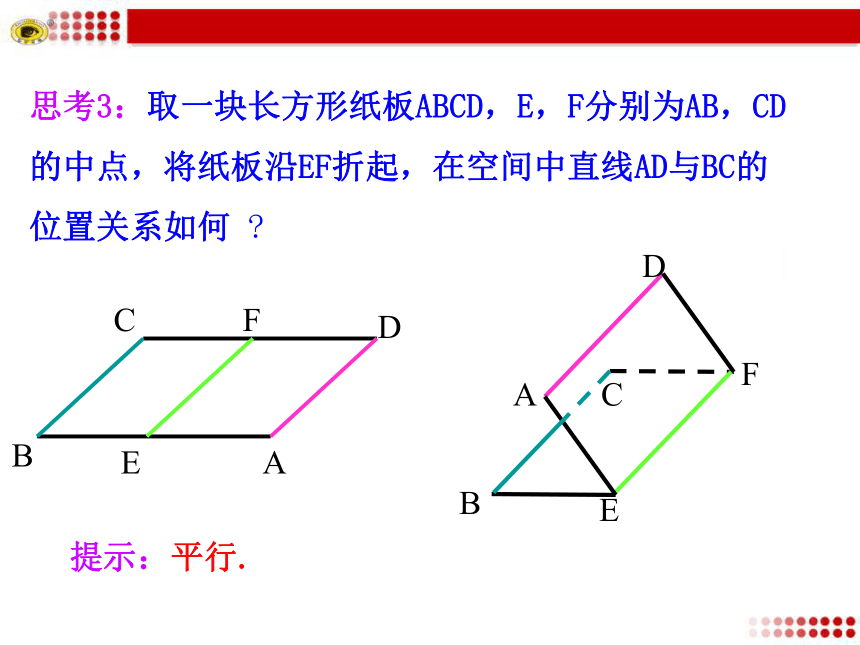
AA′,DD′∥AA′,那么BB′与DD′平行吗 ?提示:平行.思考3:取一块长方形纸板ABCD,E,F分别为AB,CD
的中点,将纸板沿EF折起,在空间中直线AD与BC的
位置关系如何 ?提示:平行.若a∥b,b∥c,提示:公理4 平行于同一条直线的两条直线平行. 则a∥c.思考4:通过上述实验可以得到什么结论?问题:观察下列图形,直线与直线的位置关系有哪些? ②①③探究点2 异面直线(2) 如图②中直线a和b在同一个平面内,但没有公共点,这样的两条直线叫作平行直线,记作:a∥b;空间两条直线的位置关系有三种:(1) 如图①中直线a和b只有一个公共点A,这样的两条直线叫作相交直线,记作:a∩b=A;(3)如图③中直线AD与直线BB1;直线AD与直线BD1,它们不同在任何一个平面内,这样的两条直线叫作异面直线.为了表示异面直线不共面的特点,作图时通常用一个或两个平面衬托,如图:【提升总结】
对于异面直线的几点认识
(1)若直线a,b 是异面直线,则在空间中找不到一个平
面,使其同时经过a,b 两条直线.
(2)不能误解为分别在不同平面内的两条直线为异面直线.
(3)画异面直线时,为了充分显示出它们既不平行又不相交的特点,常常需要以辅助平面作为衬托,以加强直观性.例1 在正方体ABCD-A1B1C1D1中,直线AB与C1D1 ,AD1与 BC1 ,AA1与CC1,AC与A1C1是什么位置关系?解: AB∥C1D1,AD1∥BC1 ,
AA1 ∥ CC1,AC∥A1C1.例2 在空间四边形ABCD中,E,F,G,H分别是边AB,BC, CD,DA的中点,求证:四边形EFGH是平行四边形.证明:如图,连接BD.
因为FG是△CBD的中位线,所以又因为EH是△ABD的中位线,所以所以四边形EFGH是平行四边形.思考1:在平面上,如果一个角的两边与另一个角的
两边分别平行,那么这两个角的大小有什么关系? 探究点3 “等角”定理提示:相等或互补.思考2: 如图,四棱柱ABCD-A′B′C′D′的底面是平
行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′
的两边分别对应平行,这两组角的大小关系如何?提示:相等.提示:互补.思考3:综上分析我们可以得到什么定理?提示:空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补.探究点4 两条异面直线所成的角如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角.若两条异面直线所成角为90°,则称它们互相垂直.异面直线a与b垂直记作:a⊥b.异面直线所成角θ的取值范围: .例3 如图,将无盖正方体纸盒展开,直线AB,CD在原
正方体中的位置关系是( ).A.平行 B.相交且垂直 C.异面直线 D.相交成60°D解:选D.将上面的展开图还原成正方体,点B与点D重合.容易知道AB=BC=CA,从而△ABC是等边三角形.所以选D.例4 在正方体ABCD-A1B1C1D1中指出下列各对线段所成的角:(1)AB与CC1.(2)A1 B1与AC.(3)A1B与D1B1.B1CC1ABDA1D1解:(1)AB与CC1所成的角等于90°.(2)A1 B1与AC所成的角等于45°.(3)A1B与D1B1所成的角等于60°.【提升总结】求异面直线所成角的步骤:异面直线所成角相交线所成的角解三角形求角(取锐角或直角)平移构造三角形即:“作—证—算—答” 注意:对于有数据的题目,要注意勾股定理,三角函数,边边关系,对于有关中点的题目要留意三角形中位线. 1.判断对错:
(1)分别在两个平面内的两条直线一定是异面直线.( )
(2)空间两条不相交的直线一定是异面直线. ( )
(3)垂直于同一条直线的两条直线必平行. ( )
(4)若一条直线垂直于两条平行直线中的一条,则它
一定与另一条直线垂直. ( ) √×××2.分别在两个平面内的两条直线的位置关系是( )
A.异面 B.平行
C.相交 D.以上都有可能【解析】选D.如图,a∥b,c与d相交,a与d异面.D3.直线a,b,c两两平行,但不共面,经过其中两条
直线的平面的个数为( )
A.1 B.3
C.6 D.0【解析】选B.以三棱柱为例,三条侧棱两两平行,但不共面,显然经过其中的两条直线的平面有3个.B1. 空间直线的平行关系及相关定理.2. 异面直线的定义及两条异面直线所成的角.3. 求异面直线所成的角的一般方法.
“作—证—算—答” 不能因为我们感觉不到温暖就否定太阳的存在;不能因为我们感觉不到真诚就否定人间真诚的存在.
2.能正确应用公理4判断空间两直线平行.(重点)
3.理解两异面直线的定义,会求两异面直线所成的角.(难点)思考1:设直线a//b,将直线a在空间中作平行移动,
在平移过程中a与b仍保持平行吗(前提是二者不重合)?探究点1 平行公理提示:平行.思考2:如图, 在长方体ABCD-A′B′C′D′中,BB′∥
AA′,DD′∥AA′,那么BB′与DD′平行吗 ?提示:平行.思考3:取一块长方形纸板ABCD,E,F分别为AB,CD
的中点,将纸板沿EF折起,在空间中直线AD与BC的
位置关系如何 ?提示:平行.若a∥b,b∥c,提示:公理4 平行于同一条直线的两条直线平行. 则a∥c.思考4:通过上述实验可以得到什么结论?问题:观察下列图形,直线与直线的位置关系有哪些? ②①③探究点2 异面直线(2) 如图②中直线a和b在同一个平面内,但没有公共点,这样的两条直线叫作平行直线,记作:a∥b;空间两条直线的位置关系有三种:(1) 如图①中直线a和b只有一个公共点A,这样的两条直线叫作相交直线,记作:a∩b=A;(3)如图③中直线AD与直线BB1;直线AD与直线BD1,它们不同在任何一个平面内,这样的两条直线叫作异面直线.为了表示异面直线不共面的特点,作图时通常用一个或两个平面衬托,如图:【提升总结】
对于异面直线的几点认识
(1)若直线a,b 是异面直线,则在空间中找不到一个平
面,使其同时经过a,b 两条直线.
(2)不能误解为分别在不同平面内的两条直线为异面直线.
(3)画异面直线时,为了充分显示出它们既不平行又不相交的特点,常常需要以辅助平面作为衬托,以加强直观性.例1 在正方体ABCD-A1B1C1D1中,直线AB与C1D1 ,AD1与 BC1 ,AA1与CC1,AC与A1C1是什么位置关系?解: AB∥C1D1,AD1∥BC1 ,
AA1 ∥ CC1,AC∥A1C1.例2 在空间四边形ABCD中,E,F,G,H分别是边AB,BC, CD,DA的中点,求证:四边形EFGH是平行四边形.证明:如图,连接BD.
因为FG是△CBD的中位线,所以又因为EH是△ABD的中位线,所以所以四边形EFGH是平行四边形.思考1:在平面上,如果一个角的两边与另一个角的
两边分别平行,那么这两个角的大小有什么关系? 探究点3 “等角”定理提示:相等或互补.思考2: 如图,四棱柱ABCD-A′B′C′D′的底面是平
行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′
的两边分别对应平行,这两组角的大小关系如何?提示:相等.提示:互补.思考3:综上分析我们可以得到什么定理?提示:空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补.探究点4 两条异面直线所成的角如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角.若两条异面直线所成角为90°,则称它们互相垂直.异面直线a与b垂直记作:a⊥b.异面直线所成角θ的取值范围: .例3 如图,将无盖正方体纸盒展开,直线AB,CD在原
正方体中的位置关系是( ).A.平行 B.相交且垂直 C.异面直线 D.相交成60°D解:选D.将上面的展开图还原成正方体,点B与点D重合.容易知道AB=BC=CA,从而△ABC是等边三角形.所以选D.例4 在正方体ABCD-A1B1C1D1中指出下列各对线段所成的角:(1)AB与CC1.(2)A1 B1与AC.(3)A1B与D1B1.B1CC1ABDA1D1解:(1)AB与CC1所成的角等于90°.(2)A1 B1与AC所成的角等于45°.(3)A1B与D1B1所成的角等于60°.【提升总结】求异面直线所成角的步骤:异面直线所成角相交线所成的角解三角形求角(取锐角或直角)平移构造三角形即:“作—证—算—答” 注意:对于有数据的题目,要注意勾股定理,三角函数,边边关系,对于有关中点的题目要留意三角形中位线. 1.判断对错:
(1)分别在两个平面内的两条直线一定是异面直线.( )
(2)空间两条不相交的直线一定是异面直线. ( )
(3)垂直于同一条直线的两条直线必平行. ( )
(4)若一条直线垂直于两条平行直线中的一条,则它
一定与另一条直线垂直. ( ) √×××2.分别在两个平面内的两条直线的位置关系是( )
A.异面 B.平行
C.相交 D.以上都有可能【解析】选D.如图,a∥b,c与d相交,a与d异面.D3.直线a,b,c两两平行,但不共面,经过其中两条
直线的平面的个数为( )
A.1 B.3
C.6 D.0【解析】选B.以三棱柱为例,三条侧棱两两平行,但不共面,显然经过其中的两条直线的平面有3个.B1. 空间直线的平行关系及相关定理.2. 异面直线的定义及两条异面直线所成的角.3. 求异面直线所成的角的一般方法.
“作—证—算—答” 不能因为我们感觉不到温暖就否定太阳的存在;不能因为我们感觉不到真诚就否定人间真诚的存在.
同课章节目录
