5.1 平行关系的判定
图片预览






文档简介
课件30张PPT。§5 平行关系
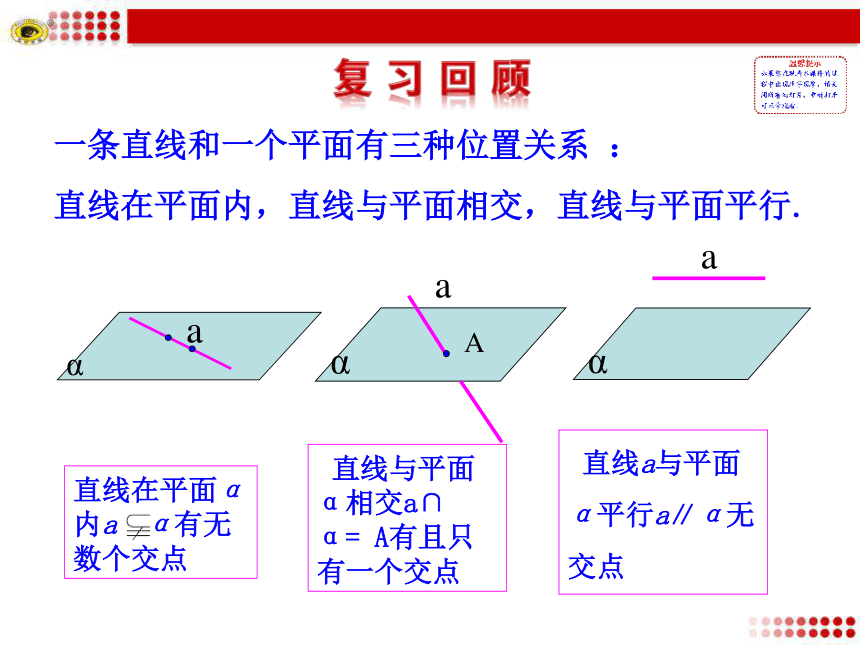
5.1 平行关系的判定 直线与平面α相交a∩ α= A有且只有一个交点 直线a与平面α平行a∥α无交点一条直线和一个平面有三种位置关系 :
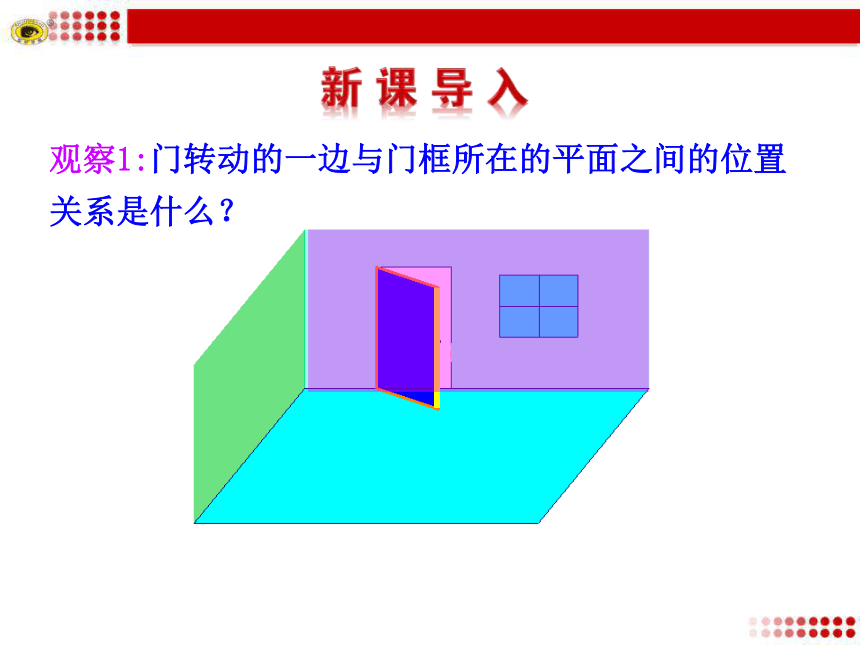
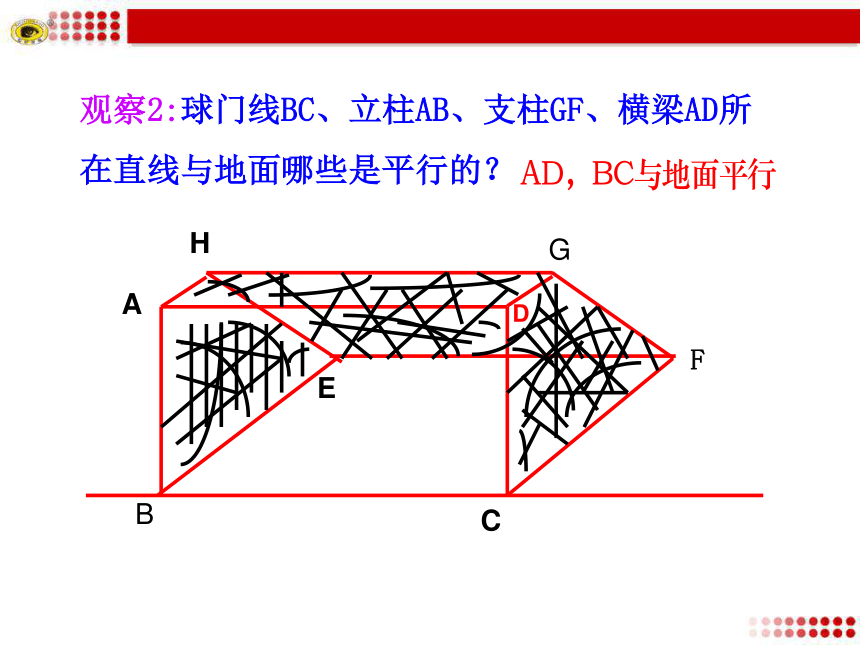
直线在平面内,直线与平面相交,直线与平面平行.直线在平面α内a α有无数个交点 观察1:门转动的一边与门框所在的平面之间的位置关系是什么?观察2:球门线BC、立柱AB、支柱GF、横梁AD所在直线与地面哪些是平行的?BADCHGE F观察3:将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?本节课我们来学习平行关系的判定!平行1.理解并掌握直线与平面平行、平面与平面平行的判定定理.(重点)
2.会用图形语言、文字语言、符号语言准确描述这两个定理,并知道其地位和作用.(重点)
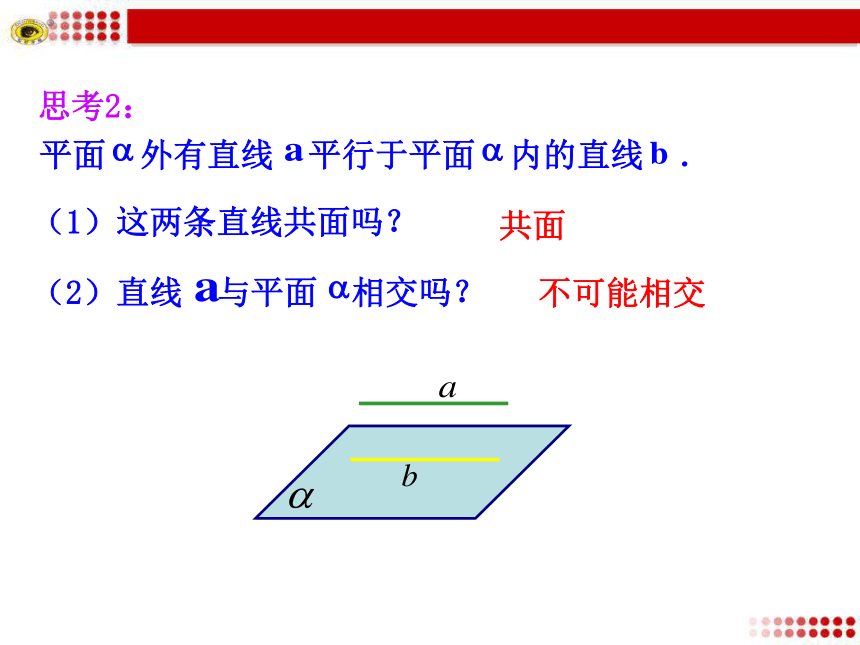
3.能运用两个定理证明线面、面面平行问题.(难点)思考1:观察下图所示的长方体,直线a与直线b有什么位置关系?直线a与平面α有什么位置关系?探究点1 直线与平面平行的判定直线a不在平面α内,直线b在平面α内,a∥b,
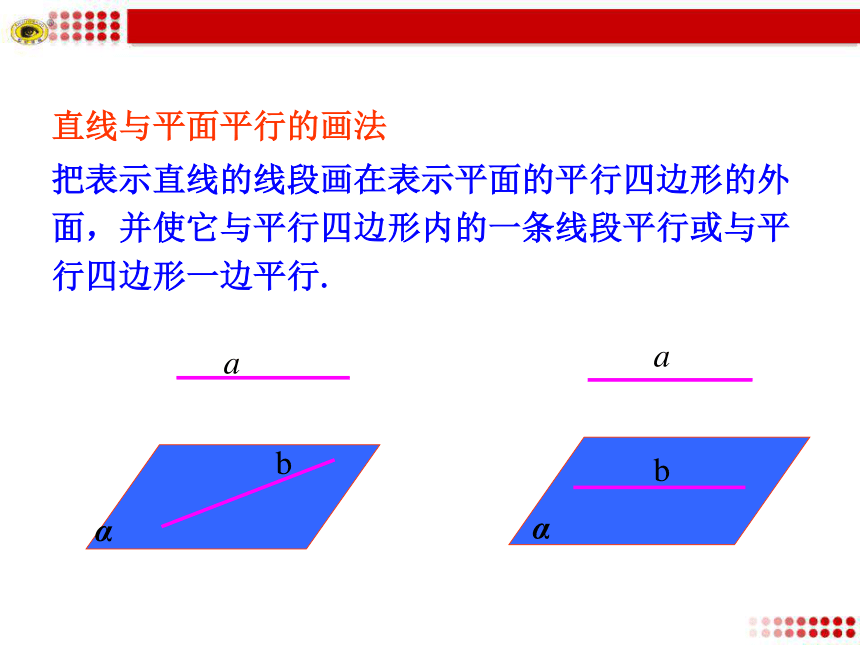
这时,a∥α.平面 外有直线 平行于平面 内的直线 .(1)这两条直线共面吗?(2)直线 与平面 相交吗?共面不可能相交思考2: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.直线和平面平行的判定定理转化到线线平行直线与平面平行的画法把表示直线的线段画在表示平面的平行四边形的外面,并使它与平行四边形内的一条线段平行或与平行四边形一边平行. 家庭中安装方形镜子时,为了使镜子的上边框与天花板平行,只需要使镜子的上边框与天花板和墙面的交线平行,显然用到了这个判定定理.
安装教室里的日光灯,也用到了这个判定定理.思考交流
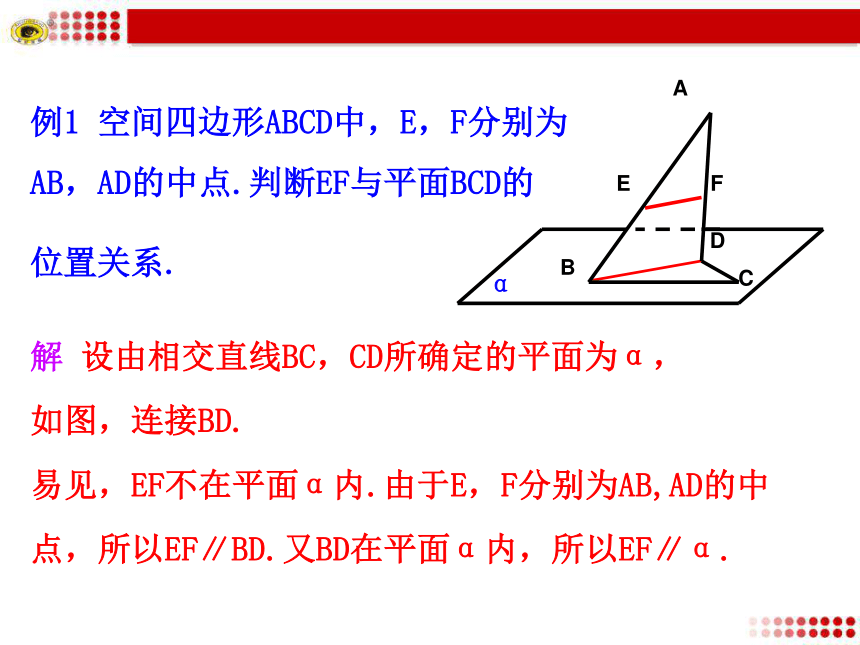
你能举出生活中应用线面平行判定定理的例子吗?例1 空间四边形ABCD中,E,F分别为 AB,AD的中点.判断EF与平面BCD的
位置关系.解 设由相交直线BC,CD所确定的平面为α,
如图,连接BD.
易见,EF不在平面α内.由于E,F分别为AB,AD的中点,所以EF∥BD.又BD在平面α内,所以EF∥α.α例2 如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.试指出图中满足线面平行位置关系的所有情况.BCEDGFAH所以,BE∥AF,BE 平面PAD,AF?平面PAD,
根据线面平行的判定定理可得BE∥平面PAD.【变式练习】如图所示,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,CD=2AB,E为PC的中点,求证BE∥平面PAD.证明:取PD的中点F,连接EF,AF,由E,F为中点,所以EF∥CD且EF= CD,又AB∥CD,CD=2AB,故EF∥AB,且EF=AB,从而四边形ABEF为平行四边形,
1. 线面平行,通常可以转化为线线平行来处理.2. 寻找平行直线可以通过三角形的中位线、梯形的中位线、平行四边形的判定来完成.3. 证明的书写:三个条件“内”、“外”、“平行” 缺一不可.证明线面平行的注意事项【提升总结】思考:空间两平面有哪些位置关系?相交平行有公共点无公共点探究点2 面面平行的判定定理思考:反之,若α中所有直线都平行β ,则α∥β启示: 两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题.若平面α∥β,则α中所有直线都平行β??平行平行平面α内有一条直线 a 平行于平面β, 则α∥β吗? 请举例说明.问题1问题2平面α内有两条直线a , b 平行于平面β, 则α∥β吗? 请举例说明.探究:不能不能模型1αβα// β?αα模型2a // βabαb//ββa // bαβab你能得到什么结论?问题3 平面α内有两条相交直线 a , b 平行平面β, 则α∥β吗?平行a?? , b??a?b =Pa // ? b // ??// ?符号语言面面平行线面平行线线平行ab?图形语言??如果一个 有两条 直线都平行于另一个平面,相交那么这两个平面平行.P平面内线不在多
贵在相交a ? , b ?例3:已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD.证明:如图,因为ABCD-A1B1C1D1
为正方体,所以 BD∥B1D1.因此,平面AB1D1∥平面C1BD.又B1D1 平面AB1D1,
从而BD∥平面AB1D1同理可证 BC1∥平面AB1D1.
又直线BD与直线BC1交于点B.C1CBAA1B1D1D1 判断下列说法是否正确:(2)若直线a//b , a//c ,且 ,则 .( )(1)若直线a与平面 内的一条直线平行 ,则 a
与平面 平行 . ( ) (4)如果直线和平面平行,那么直线和平面内的所有直线平行.( )(3)如果直线和平面平行,那么直线和平面内的无数条直线平行.( )××√×2.下面四个正方体图形中,A,B为正方体的两个顶
点,M,N,P分别为其所在棱的中点,能得出AB//平
面MNP的图形是( )
A.③④?????B.①②?? C.②③????D.①④3.α,β是两个不重合的平面,a,b是两条不同直
线,在下列条件下,可判定α∥β的是( )A.α,β都平行于直线a,bB.α内有三个不共线点到β的距离相等C.a,b是α内两条直线,且a∥β,b∥βD.a,b是两条异面直线且a∥α,b∥α,a∥β,b∥β解:A错,若a∥b,则不能断定α∥β;B错,若A,B,C三点不在β的同一侧,则不能断定α∥β; C错,若a∥b,则不能断定α∥β.故选D. D4.已知正方体ABCD-A1B1C1D1,P,Q,R分别为A1A,AB,AD的中点 .求证:平面PQR∥平面CB1D1.证明:连接A1B,BD.
因为PQ∥A1B且A1B ∥CD1.
故PQ∥CD1.
同理可得,RQ//B1D1.
所以平面PQR∥平面CB1D1.A1B1C1D11.线面平行的判定定理:线线平行线面平行(将空间问题转化为平面问题)2.线面平行的判定方法:平行移动法3.面面平行的定义;4.面面平行的判定定理;5.面面平行判定定理的应用:
线线、线面、面面间的位置关系的转化. 不能因为人生的道路坎坷,就使自己的身躯变得弯曲;不能因为生活的历程漫长,就使求索的脚步迟缓.
5.1 平行关系的判定 直线与平面α相交a∩ α= A有且只有一个交点 直线a与平面α平行a∥α无交点一条直线和一个平面有三种位置关系 :
直线在平面内,直线与平面相交,直线与平面平行.直线在平面α内a α有无数个交点 观察1:门转动的一边与门框所在的平面之间的位置关系是什么?观察2:球门线BC、立柱AB、支柱GF、横梁AD所在直线与地面哪些是平行的?BADCHGE F观察3:将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?本节课我们来学习平行关系的判定!平行1.理解并掌握直线与平面平行、平面与平面平行的判定定理.(重点)
2.会用图形语言、文字语言、符号语言准确描述这两个定理,并知道其地位和作用.(重点)
3.能运用两个定理证明线面、面面平行问题.(难点)思考1:观察下图所示的长方体,直线a与直线b有什么位置关系?直线a与平面α有什么位置关系?探究点1 直线与平面平行的判定直线a不在平面α内,直线b在平面α内,a∥b,
这时,a∥α.平面 外有直线 平行于平面 内的直线 .(1)这两条直线共面吗?(2)直线 与平面 相交吗?共面不可能相交思考2: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.直线和平面平行的判定定理转化到线线平行直线与平面平行的画法把表示直线的线段画在表示平面的平行四边形的外面,并使它与平行四边形内的一条线段平行或与平行四边形一边平行. 家庭中安装方形镜子时,为了使镜子的上边框与天花板平行,只需要使镜子的上边框与天花板和墙面的交线平行,显然用到了这个判定定理.
安装教室里的日光灯,也用到了这个判定定理.思考交流
你能举出生活中应用线面平行判定定理的例子吗?例1 空间四边形ABCD中,E,F分别为 AB,AD的中点.判断EF与平面BCD的
位置关系.解 设由相交直线BC,CD所确定的平面为α,
如图,连接BD.
易见,EF不在平面α内.由于E,F分别为AB,AD的中点,所以EF∥BD.又BD在平面α内,所以EF∥α.α例2 如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.试指出图中满足线面平行位置关系的所有情况.BCEDGFAH所以,BE∥AF,BE 平面PAD,AF?平面PAD,
根据线面平行的判定定理可得BE∥平面PAD.【变式练习】如图所示,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,CD=2AB,E为PC的中点,求证BE∥平面PAD.证明:取PD的中点F,连接EF,AF,由E,F为中点,所以EF∥CD且EF= CD,又AB∥CD,CD=2AB,故EF∥AB,且EF=AB,从而四边形ABEF为平行四边形,
1. 线面平行,通常可以转化为线线平行来处理.2. 寻找平行直线可以通过三角形的中位线、梯形的中位线、平行四边形的判定来完成.3. 证明的书写:三个条件“内”、“外”、“平行” 缺一不可.证明线面平行的注意事项【提升总结】思考:空间两平面有哪些位置关系?相交平行有公共点无公共点探究点2 面面平行的判定定理思考:反之,若α中所有直线都平行β ,则α∥β启示: 两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题.若平面α∥β,则α中所有直线都平行β??平行平行平面α内有一条直线 a 平行于平面β, 则α∥β吗? 请举例说明.问题1问题2平面α内有两条直线a , b 平行于平面β, 则α∥β吗? 请举例说明.探究:不能不能模型1αβα// β?αα模型2a // βabαb//ββa // bαβab你能得到什么结论?问题3 平面α内有两条相交直线 a , b 平行平面β, 则α∥β吗?平行a?? , b??a?b =Pa // ? b // ??// ?符号语言面面平行线面平行线线平行ab?图形语言??如果一个 有两条 直线都平行于另一个平面,相交那么这两个平面平行.P平面内线不在多
贵在相交a ? , b ?例3:已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD.证明:如图,因为ABCD-A1B1C1D1
为正方体,所以 BD∥B1D1.因此,平面AB1D1∥平面C1BD.又B1D1 平面AB1D1,
从而BD∥平面AB1D1同理可证 BC1∥平面AB1D1.
又直线BD与直线BC1交于点B.C1CBAA1B1D1D1 判断下列说法是否正确:(2)若直线a//b , a//c ,且 ,则 .( )(1)若直线a与平面 内的一条直线平行 ,则 a
与平面 平行 . ( ) (4)如果直线和平面平行,那么直线和平面内的所有直线平行.( )(3)如果直线和平面平行,那么直线和平面内的无数条直线平行.( )××√×2.下面四个正方体图形中,A,B为正方体的两个顶
点,M,N,P分别为其所在棱的中点,能得出AB//平
面MNP的图形是( )
A.③④?????B.①②?? C.②③????D.①④3.α,β是两个不重合的平面,a,b是两条不同直
线,在下列条件下,可判定α∥β的是( )A.α,β都平行于直线a,bB.α内有三个不共线点到β的距离相等C.a,b是α内两条直线,且a∥β,b∥βD.a,b是两条异面直线且a∥α,b∥α,a∥β,b∥β解:A错,若a∥b,则不能断定α∥β;B错,若A,B,C三点不在β的同一侧,则不能断定α∥β; C错,若a∥b,则不能断定α∥β.故选D. D4.已知正方体ABCD-A1B1C1D1,P,Q,R分别为A1A,AB,AD的中点 .求证:平面PQR∥平面CB1D1.证明:连接A1B,BD.
因为PQ∥A1B且A1B ∥CD1.
故PQ∥CD1.
同理可得,RQ//B1D1.
所以平面PQR∥平面CB1D1.A1B1C1D11.线面平行的判定定理:线线平行线面平行(将空间问题转化为平面问题)2.线面平行的判定方法:平行移动法3.面面平行的定义;4.面面平行的判定定理;5.面面平行判定定理的应用:
线线、线面、面面间的位置关系的转化. 不能因为人生的道路坎坷,就使自己的身躯变得弯曲;不能因为生活的历程漫长,就使求索的脚步迟缓.
同课章节目录
