5.2 第2课时 平面与平面平行的性质
文档属性
| 名称 | 5.2 第2课时 平面与平面平行的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 00:00:00 | ||
图片预览



文档简介
课件23张PPT。第2课时 平面与平面平行的性质回想一下,平面与平面平行的判定定理是什么?
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行 平面与平面平行的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的前提下,可以得到什么结论呢?请进入本节课的学习!1.掌握平面与平面平行的性质,并会应用性质解决问题.(重点)
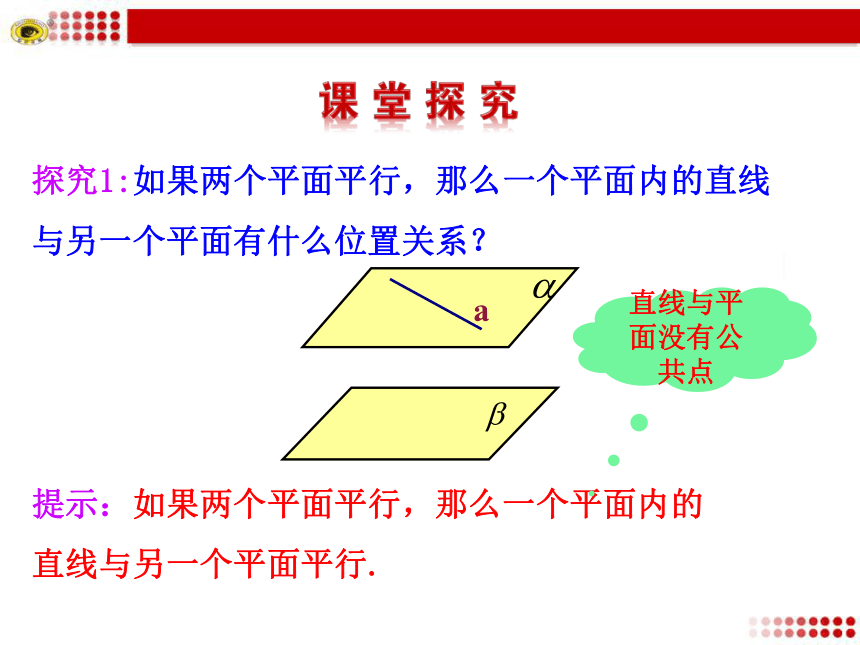
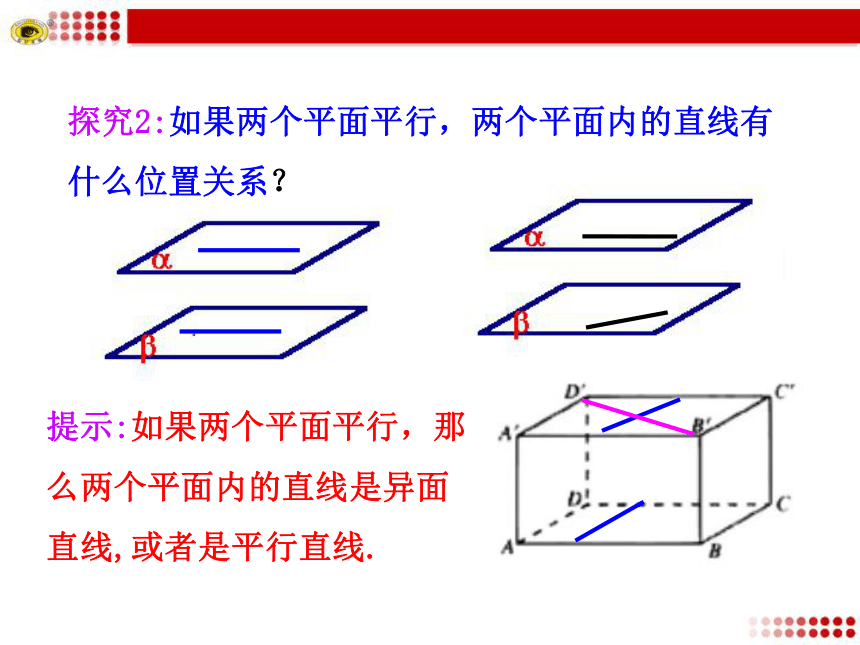
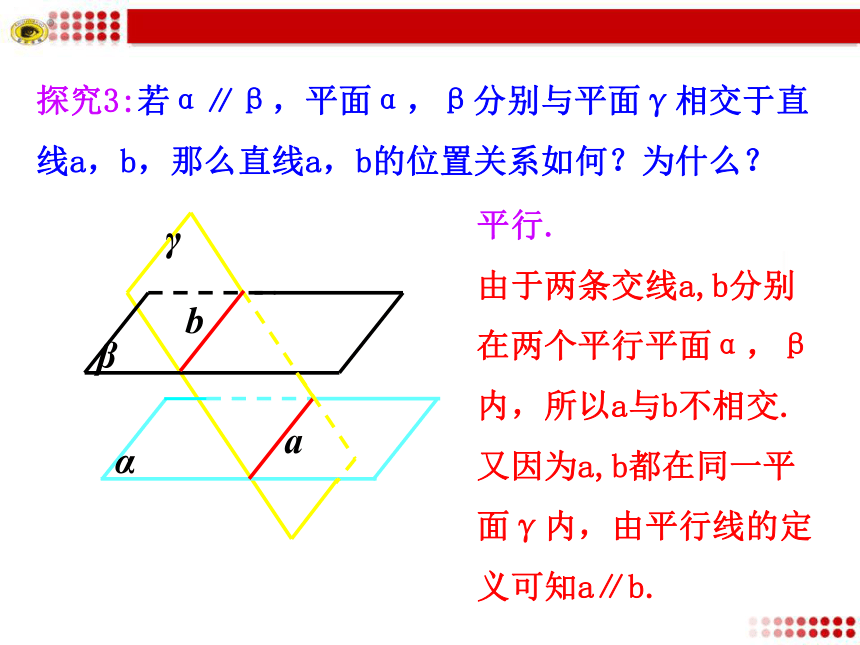
2.能运用平面与平面平行的性质定理证明一些空间平行关系的简单问题.(难点)探究1:如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?提示:如果两个平面平行,那么一个平面内的直线与另一个平面平行.直线与平面没有公共点探究2:如果两个平面平行,两个平面内的直线有什么位置关系?提示:如果两个平面平行,那么两个平面内的直线是异面直线,或者是平行直线.探究3:若α∥β,平面α,β分别与平面γ相交于直线a,b,那么直线a,b的位置关系如何?为什么?平行.
由于两条交线a,b分别在两个平行平面α,β内,所以a与b不相交.
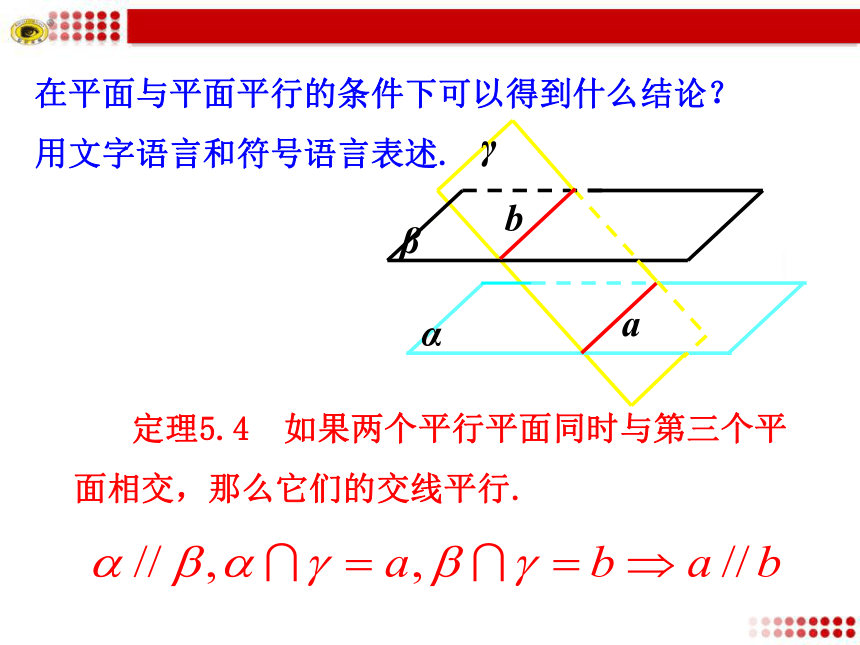
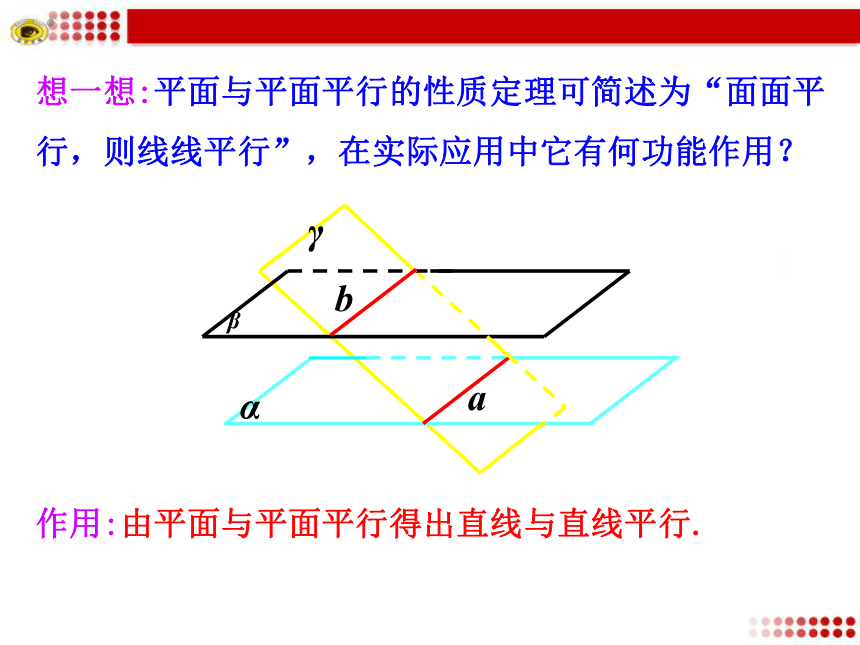
又因为a,b都在同一平面γ内,由平行线的定义可知a∥b.在平面与平面平行的条件下可以得到什么结论?用文字语言和符号语言表述. 定理5.4 如果两个平行平面同时与第三个平面相交,那么它们的交线平行.想一想:平面与平面平行的性质定理可简述为“面面平行,则线线平行”,在实际应用中它有何功能作用?作用:由平面与平面平行得出直线与直线平行.直线与直线平行平面与平面平行面面平行的判定定理面面平行的性质定理例1.?求证:夹在两个平行平面间的平行线段相等.如图,α//β,AB//CD,且A∈α,
C∈α,B∈β,D∈β.
求证:AB=CD.证明 因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交于AC和BD.因为α//β,所以AC//BD. 因此,四边形ABDC是平行四边形.所以AB=CD.提示:
1.若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2.平行于同一平面的两平面平行;
3.夹在两平行平面间的平行线段相等.想一想:由两个平面平行可以得到哪些结论呢?例2 如图,平面α,β,γ两两平行,且直线l与α,β,γ分别相交于点A,B,C,直线m与α,β,γ分别相交于点D,E,F,AB=6,BC=2,EF=3.求DE的长.BE解 当直线m与l共面时,该平面与α,β,γ分别交于直线AD,BE,CF,因为α,β,γ两两平行,所以AD∥BE∥CF,故当直线m与l不共面时,连接DC.
设DC与β相交于点G,则平面ACD与α,β分别相交于直线AD,BG,平面DCF与β,γ分别相交于直线GE,CF.因为α,β,γ两两平行,所以BG∥AD,GE∥CF.
因此所以 又因为AB=6,BC=2,EF=3,所以,DE=9.1.已知直线a?α,给出以下三个叙述: ①若平面α∥平面β,则直线a∥平面β; ②若直线a∥平面β,则平面α∥平面β; ③若直线a不平行于平面β,则平面α不平行于平面β.其中正确的是( )A.② B.③C. ①② D.①③D解:①若平面α∥平面β,则直线a∥平面β;因为直线a?α,平面α∥平面β,则α内的每一条直线都平行平面β.显然正确.②若直线a∥平面β,则平面α∥平面β;因为当平面α与平面β相交的时候,仍然可以存在直线a?α使直线a∥平面β.故错误.③若直线a不平行于平面β,则平面α不平行于平面β;平面内有一条直线不平行于另一个平面,两平面就不会平行.故显然正确.2.若平面α∥平面β,直线a∥α,点B∈β,则在β
内过点B的所有直线中( )
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线
提示:若a在β内且B在a上,则不存在直线与a平行.A3.已知平面α∥平面β,若两条直线m,n分别在平面α,β内,则直线m,n的关系不可能是________.
【解析】若两条直线相交,则平面α与平面β有公共点,与α∥β矛盾,故两条直线不可能相交.相交4.过正方体ABCD-A1B1C1D1的三顶点A1,C1,B的平面
与底面ABCD所在平面的交线为l,则l与A1C1的位置关
系是_____.
【解析】因为平面ABCD∥平面A1B1C1D1,
平面ABCD∩平面A1C1B=l,
平面A1B1C1D1∩平面A1C1B=A1C1,所以l∥A1C1.平行5.在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线B′M与平面A′BD的位置关系,并说明理由. 【解析】直线B′M//平面A′BD.理由:
连接B′C, B′D′因为B′D′//BD, B′C//A′D,
又B′D′与B′C交于B′,
BD与A′D交于D,
所以,平面A′BD//平面B′D′C.
B′M在平面B′D′C内,
所以B′M//平面A′BD. 6. 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.M【证明】取AB中点为N,连接MN,DN,
因为M是AE的中点,所以MN∥BE.
因为△ABD是等边三角形,
所以DN⊥AB.
由CB=CD,∠BCD=120°知,∠CBD=30°,
所以∠ABC=60°+30°=90°,即BC⊥AB,
所以ND∥BC,又因为MN∩DN=N,BE∩BC=B,
所以平面MND∥平面BEC,
故DM∥平面BEC. 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.面面平行的判定定理面面平行的性质定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行. 不能说凡是合理的都是美的,但凡是美的确实都是合理的.
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行 平面与平面平行的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的前提下,可以得到什么结论呢?请进入本节课的学习!1.掌握平面与平面平行的性质,并会应用性质解决问题.(重点)
2.能运用平面与平面平行的性质定理证明一些空间平行关系的简单问题.(难点)探究1:如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?提示:如果两个平面平行,那么一个平面内的直线与另一个平面平行.直线与平面没有公共点探究2:如果两个平面平行,两个平面内的直线有什么位置关系?提示:如果两个平面平行,那么两个平面内的直线是异面直线,或者是平行直线.探究3:若α∥β,平面α,β分别与平面γ相交于直线a,b,那么直线a,b的位置关系如何?为什么?平行.
由于两条交线a,b分别在两个平行平面α,β内,所以a与b不相交.
又因为a,b都在同一平面γ内,由平行线的定义可知a∥b.在平面与平面平行的条件下可以得到什么结论?用文字语言和符号语言表述. 定理5.4 如果两个平行平面同时与第三个平面相交,那么它们的交线平行.想一想:平面与平面平行的性质定理可简述为“面面平行,则线线平行”,在实际应用中它有何功能作用?作用:由平面与平面平行得出直线与直线平行.直线与直线平行平面与平面平行面面平行的判定定理面面平行的性质定理例1.?求证:夹在两个平行平面间的平行线段相等.如图,α//β,AB//CD,且A∈α,
C∈α,B∈β,D∈β.
求证:AB=CD.证明 因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交于AC和BD.因为α//β,所以AC//BD. 因此,四边形ABDC是平行四边形.所以AB=CD.提示:
1.若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2.平行于同一平面的两平面平行;
3.夹在两平行平面间的平行线段相等.想一想:由两个平面平行可以得到哪些结论呢?例2 如图,平面α,β,γ两两平行,且直线l与α,β,γ分别相交于点A,B,C,直线m与α,β,γ分别相交于点D,E,F,AB=6,BC=2,EF=3.求DE的长.BE解 当直线m与l共面时,该平面与α,β,γ分别交于直线AD,BE,CF,因为α,β,γ两两平行,所以AD∥BE∥CF,故当直线m与l不共面时,连接DC.
设DC与β相交于点G,则平面ACD与α,β分别相交于直线AD,BG,平面DCF与β,γ分别相交于直线GE,CF.因为α,β,γ两两平行,所以BG∥AD,GE∥CF.
因此所以 又因为AB=6,BC=2,EF=3,所以,DE=9.1.已知直线a?α,给出以下三个叙述: ①若平面α∥平面β,则直线a∥平面β; ②若直线a∥平面β,则平面α∥平面β; ③若直线a不平行于平面β,则平面α不平行于平面β.其中正确的是( )A.② B.③C. ①② D.①③D解:①若平面α∥平面β,则直线a∥平面β;因为直线a?α,平面α∥平面β,则α内的每一条直线都平行平面β.显然正确.②若直线a∥平面β,则平面α∥平面β;因为当平面α与平面β相交的时候,仍然可以存在直线a?α使直线a∥平面β.故错误.③若直线a不平行于平面β,则平面α不平行于平面β;平面内有一条直线不平行于另一个平面,两平面就不会平行.故显然正确.2.若平面α∥平面β,直线a∥α,点B∈β,则在β
内过点B的所有直线中( )
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线
提示:若a在β内且B在a上,则不存在直线与a平行.A3.已知平面α∥平面β,若两条直线m,n分别在平面α,β内,则直线m,n的关系不可能是________.
【解析】若两条直线相交,则平面α与平面β有公共点,与α∥β矛盾,故两条直线不可能相交.相交4.过正方体ABCD-A1B1C1D1的三顶点A1,C1,B的平面
与底面ABCD所在平面的交线为l,则l与A1C1的位置关
系是_____.
【解析】因为平面ABCD∥平面A1B1C1D1,
平面ABCD∩平面A1C1B=l,
平面A1B1C1D1∩平面A1C1B=A1C1,所以l∥A1C1.平行5.在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线B′M与平面A′BD的位置关系,并说明理由. 【解析】直线B′M//平面A′BD.理由:
连接B′C, B′D′因为B′D′//BD, B′C//A′D,
又B′D′与B′C交于B′,
BD与A′D交于D,
所以,平面A′BD//平面B′D′C.
B′M在平面B′D′C内,
所以B′M//平面A′BD. 6. 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.M【证明】取AB中点为N,连接MN,DN,
因为M是AE的中点,所以MN∥BE.
因为△ABD是等边三角形,
所以DN⊥AB.
由CB=CD,∠BCD=120°知,∠CBD=30°,
所以∠ABC=60°+30°=90°,即BC⊥AB,
所以ND∥BC,又因为MN∩DN=N,BE∩BC=B,
所以平面MND∥平面BEC,
故DM∥平面BEC. 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.面面平行的判定定理面面平行的性质定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行. 不能说凡是合理的都是美的,但凡是美的确实都是合理的.
同课章节目录
