6.1 第2课时 平面与平面垂直的判定
文档属性
| 名称 | 6.1 第2课时 平面与平面垂直的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 08:34:30 | ||
图片预览







文档简介
课件28张PPT。第2课时 平面与平面垂直的判定问题1:平面几何中“角”是怎样定义的?问题2:在立体几何中,“异面直线所成的角”、“直线和平面所成的角”有什么共同的特征?有公共顶点的两条射线所形成的图形转化为平面上的角问题3:在生产实践中,有许多问题要涉及两个平面相交所成的角的情形,你能举出这个问题的一些例子吗?这样的角有何特点,该如何表示呢?请进入本节课的学习!堤坝面与河底水平面,
打开的笔记本电脑1.理解二面角及其平面角的概念,掌握二面角的平面角的一般作法,会求简单的二面角的平面角.(难点)
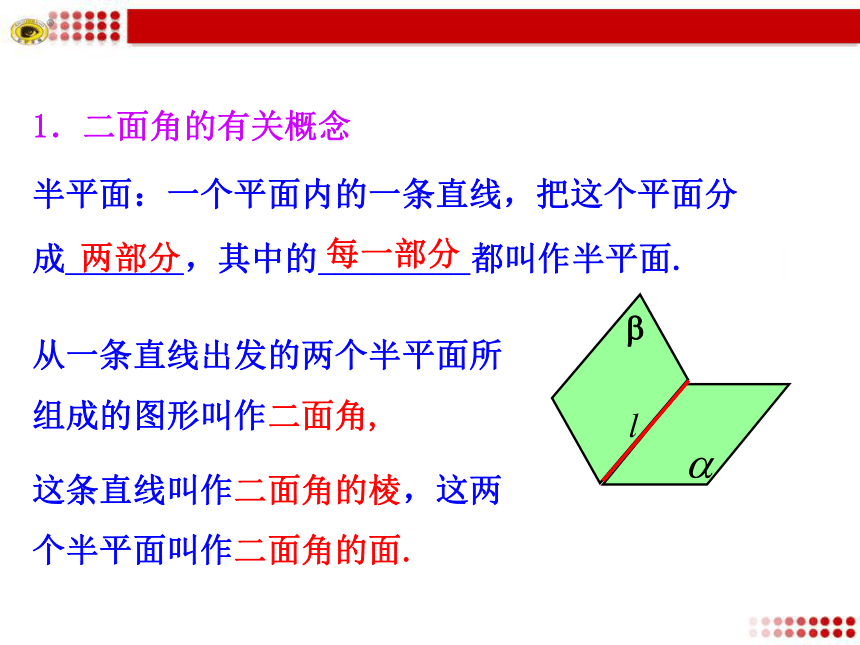
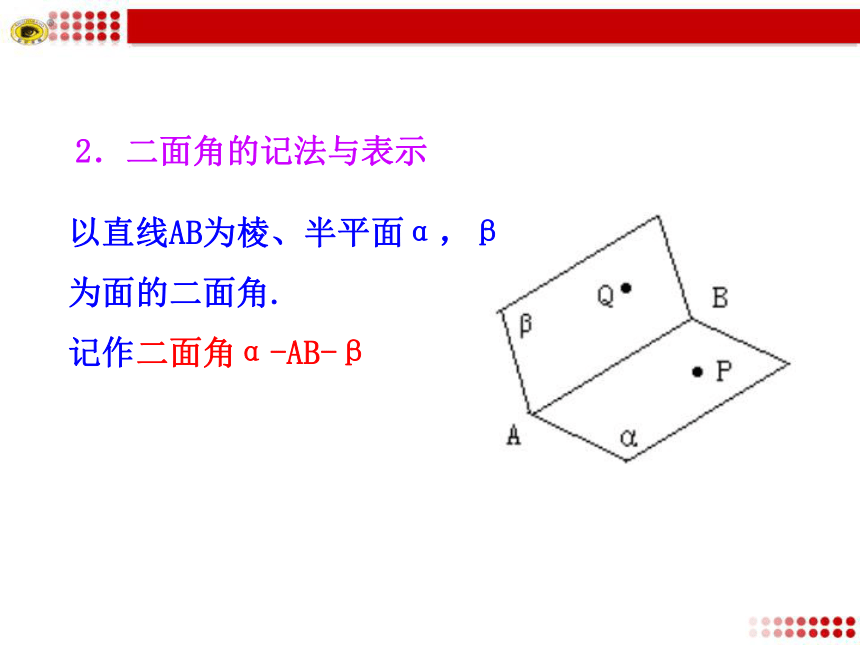
2.掌握两个平面互相垂直的概念和判定定理,能用定义和定理判定面面垂直.(重点) 展示一张纸面,并对折观察其形状,将它与角进行类比.探究点1 二面角1.二面角的有关概念从一条直线出发的两个半平面所组成的图形叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.?半平面:一个平面内的一条直线,把这个平面分成_______,其中的_________都叫作半平面.两部分每一部分2.二面角的记法与表示思考:二面角的大小反映了两个平面相交的位置关系,如我们常说“把门开大一些”,是指二面角大一些,那我们应如何度量二面角的大小呢?
提示:以二面角的棱上任一点
为端点,在两个半平面内分别
作垂直于棱的两条射线,这两条射
线所成的角叫作二面角的平面角,如图中的思考交流1.两个平面互相垂直的定义
两个平面相交,如果所成的二面角是__________,
就说这两个平面互相垂直.探究点2 平面与平面垂直直二面角平面α与β垂直,记作:α⊥β2.两个平面互相垂直的画法及其表示:问题1:根据定义判断两个平面是否垂直需要解决什么问题?
提示:两个平面所成的角是否为直二面角问题2:如图,∠AOB为直二面角α-l-β的平面角,那么直线AO与平面α的位置关系如何?αβABOl垂直探究点3 平面与平面垂直的判定两个平面垂直的判定定理:定理6.2:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.注:这个定理简称
“线面垂直,则面面垂直.”转化为线与面垂直?证明:设α∩β=CD,则B∈CD.所以AB⊥CD.在平面β内过点B作直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角,又AB⊥BE,即二面角α-CD-β是直二面角.所以α⊥β.? 两个平面垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出一个平面垂直于另一个平面的依据.特别提醒:如:建筑工人砌墙时,沿系有铅锤的线砌墙例:如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,C为⊙O上异于A,B的一点.
求证:平面PAC⊥平面PBC.证明:设⊙O所在平面为α,
由已知条件,有PA⊥α,BC在α内,
所以,PA⊥BC.
因为,点C是不同于A,B的任意
一点,AB为⊙O的直径,
所以,∠BCA=90°,即BC⊥CA.
又因为PA与AC是△PAC所在平面内的两条相交直线,
所以,BC⊥平面PAC,
又因为BC在平面PBC内,
所以,平面PAC⊥平面PBC.思考:你还能发现哪些面互相垂直?【变式练习】三棱锥P-ABC中∠ABC=90°,PA=PB=PC,则下列说法正确的是( )A.平面PAC⊥平面ABCB.平面PAB⊥平面PBCC.PB⊥平面ABCD.BC⊥平面PAB 解析:如图,因为∠ABC=90°,PA=PB=PC,所以点P在底面的射影落在△ABC的斜边的中点O处,连接OB,OP,则PO⊥OB.又因为PA=PC,所以PO⊥AC,且AC∩OB=O,所以PO⊥平面ABC.又所以PO?
平面PAC,所以平面PAC⊥平面ABC.A1.二面角指的是( )
A.从一条直线出发的两个半平面所夹的角度
B.从一条直线出发的两个半平面所组成的图形
C.两个平面相交时,两个平面所夹的锐角
D.过棱上一点和棱垂直的两条射线所成的角B2.判断正误(1)如果平面α内有一条直线垂直于平面β内的一条
直线,则α⊥β.( )(2)如果平面α内有一条直线垂直于平面β内的两条直
线,则α⊥β.( )(3) 如果平面α内的一条直线垂直于平面β内的两条
相交直线, 则α⊥β.( )××√3.直三棱柱ABC-A′B′C′中,底面三角形ABC为正
三角形,则两侧面AA′C′C与AA′B′B所成二面角
的大小为_______.60°4. 如图,在四棱锥P-ABCD中,底面ABCD是矩形, ,PD=CD=2 .
(1)求异面直线PA与BC所成角的正切值.
(2)证明:平面PDC⊥平面ABCD. 【解析】(1)在四棱锥中,因为底面是矩形,所以AD=BC,且AD∥BC,又因为AD⊥PD,故∠PAD(或其补角)是异面直线PA与BC所成的角. 在直角△PDA中, ,所以异面直线PA与BC所成角的正切值为2. (2)由于底面ABCD是矩形,因此AD⊥CD,
又由于AD⊥PD, CD∩PD=D,
因此AD⊥平面PDC,而AD在平面ABCD中,
所以平面PDC⊥平面ABCD. 1.二面角的定义及度量.2.判断两个平面垂直的方法.
①定义法②根据面面垂直的判定定理
3.从面面垂直的判定定理我们还可以看出面面垂直的问题可以转化为线面垂直的问题来解决. 不能把希望叫做白日做梦,也不能把白日之梦叫做希望.
打开的笔记本电脑1.理解二面角及其平面角的概念,掌握二面角的平面角的一般作法,会求简单的二面角的平面角.(难点)
2.掌握两个平面互相垂直的概念和判定定理,能用定义和定理判定面面垂直.(重点) 展示一张纸面,并对折观察其形状,将它与角进行类比.探究点1 二面角1.二面角的有关概念从一条直线出发的两个半平面所组成的图形叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.?半平面:一个平面内的一条直线,把这个平面分成_______,其中的_________都叫作半平面.两部分每一部分2.二面角的记法与表示思考:二面角的大小反映了两个平面相交的位置关系,如我们常说“把门开大一些”,是指二面角大一些,那我们应如何度量二面角的大小呢?
提示:以二面角的棱上任一点
为端点,在两个半平面内分别
作垂直于棱的两条射线,这两条射
线所成的角叫作二面角的平面角,如图中的思考交流1.两个平面互相垂直的定义
两个平面相交,如果所成的二面角是__________,
就说这两个平面互相垂直.探究点2 平面与平面垂直直二面角平面α与β垂直,记作:α⊥β2.两个平面互相垂直的画法及其表示:问题1:根据定义判断两个平面是否垂直需要解决什么问题?
提示:两个平面所成的角是否为直二面角问题2:如图,∠AOB为直二面角α-l-β的平面角,那么直线AO与平面α的位置关系如何?αβABOl垂直探究点3 平面与平面垂直的判定两个平面垂直的判定定理:定理6.2:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.注:这个定理简称
“线面垂直,则面面垂直.”转化为线与面垂直?证明:设α∩β=CD,则B∈CD.所以AB⊥CD.在平面β内过点B作直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角,又AB⊥BE,即二面角α-CD-β是直二面角.所以α⊥β.? 两个平面垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出一个平面垂直于另一个平面的依据.特别提醒:如:建筑工人砌墙时,沿系有铅锤的线砌墙例:如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,C为⊙O上异于A,B的一点.
求证:平面PAC⊥平面PBC.证明:设⊙O所在平面为α,
由已知条件,有PA⊥α,BC在α内,
所以,PA⊥BC.
因为,点C是不同于A,B的任意
一点,AB为⊙O的直径,
所以,∠BCA=90°,即BC⊥CA.
又因为PA与AC是△PAC所在平面内的两条相交直线,
所以,BC⊥平面PAC,
又因为BC在平面PBC内,
所以,平面PAC⊥平面PBC.思考:你还能发现哪些面互相垂直?【变式练习】三棱锥P-ABC中∠ABC=90°,PA=PB=PC,则下列说法正确的是( )A.平面PAC⊥平面ABCB.平面PAB⊥平面PBCC.PB⊥平面ABCD.BC⊥平面PAB 解析:如图,因为∠ABC=90°,PA=PB=PC,所以点P在底面的射影落在△ABC的斜边的中点O处,连接OB,OP,则PO⊥OB.又因为PA=PC,所以PO⊥AC,且AC∩OB=O,所以PO⊥平面ABC.又所以PO?
平面PAC,所以平面PAC⊥平面ABC.A1.二面角指的是( )
A.从一条直线出发的两个半平面所夹的角度
B.从一条直线出发的两个半平面所组成的图形
C.两个平面相交时,两个平面所夹的锐角
D.过棱上一点和棱垂直的两条射线所成的角B2.判断正误(1)如果平面α内有一条直线垂直于平面β内的一条
直线,则α⊥β.( )(2)如果平面α内有一条直线垂直于平面β内的两条直
线,则α⊥β.( )(3) 如果平面α内的一条直线垂直于平面β内的两条
相交直线, 则α⊥β.( )××√3.直三棱柱ABC-A′B′C′中,底面三角形ABC为正
三角形,则两侧面AA′C′C与AA′B′B所成二面角
的大小为_______.60°4. 如图,在四棱锥P-ABCD中,底面ABCD是矩形, ,PD=CD=2 .
(1)求异面直线PA与BC所成角的正切值.
(2)证明:平面PDC⊥平面ABCD. 【解析】(1)在四棱锥中,因为底面是矩形,所以AD=BC,且AD∥BC,又因为AD⊥PD,故∠PAD(或其补角)是异面直线PA与BC所成的角. 在直角△PDA中, ,所以异面直线PA与BC所成角的正切值为2. (2)由于底面ABCD是矩形,因此AD⊥CD,
又由于AD⊥PD, CD∩PD=D,
因此AD⊥平面PDC,而AD在平面ABCD中,
所以平面PDC⊥平面ABCD. 1.二面角的定义及度量.2.判断两个平面垂直的方法.
①定义法②根据面面垂直的判定定理
3.从面面垂直的判定定理我们还可以看出面面垂直的问题可以转化为线面垂直的问题来解决. 不能把希望叫做白日做梦,也不能把白日之梦叫做希望.
同课章节目录
