6.2 第1课时 直线与平面垂直的性质
文档属性
| 名称 | 6.2 第1课时 直线与平面垂直的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 08:52:16 | ||
图片预览





文档简介
课件23张PPT。6.2 垂直关系的性质
第1课时 直线与平面垂直的性质前面我们学习了:
1.直线与平面垂直的定义;
判定直线与平面垂直的方法.
2.直线与平面垂直的判定定理,解决了直线与平面垂直的问题;反之,在直线与平面垂直的条件下,能得到哪些结论?图中立柱与地面是垂直的,你能得出什么结论?立柱相互平行国旗杆与地面都是垂直的,你能发现什么现象?旗杆互相平行1.理解直线与平面垂直的性质定理,并能用文字、符号和图形语言描述定理. (重点)
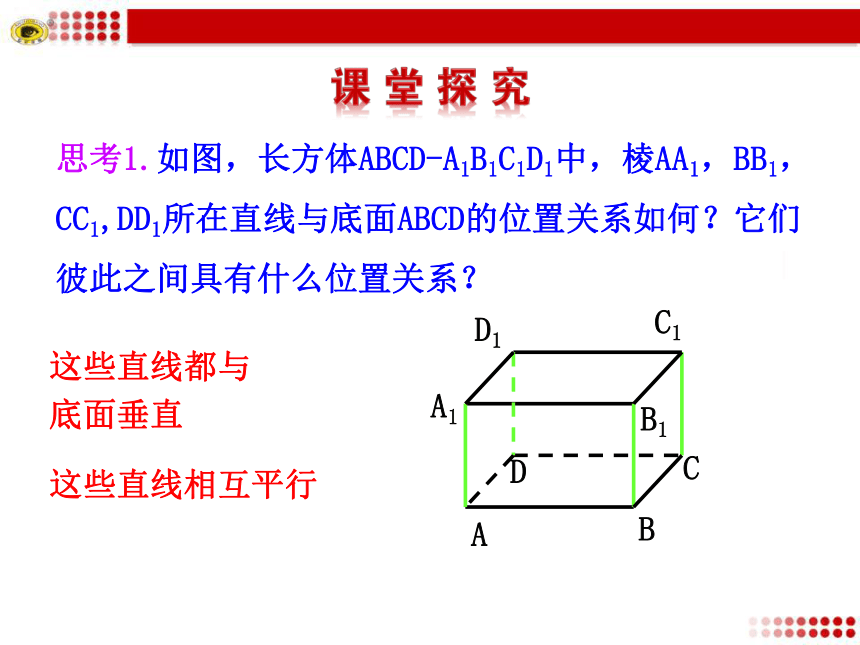
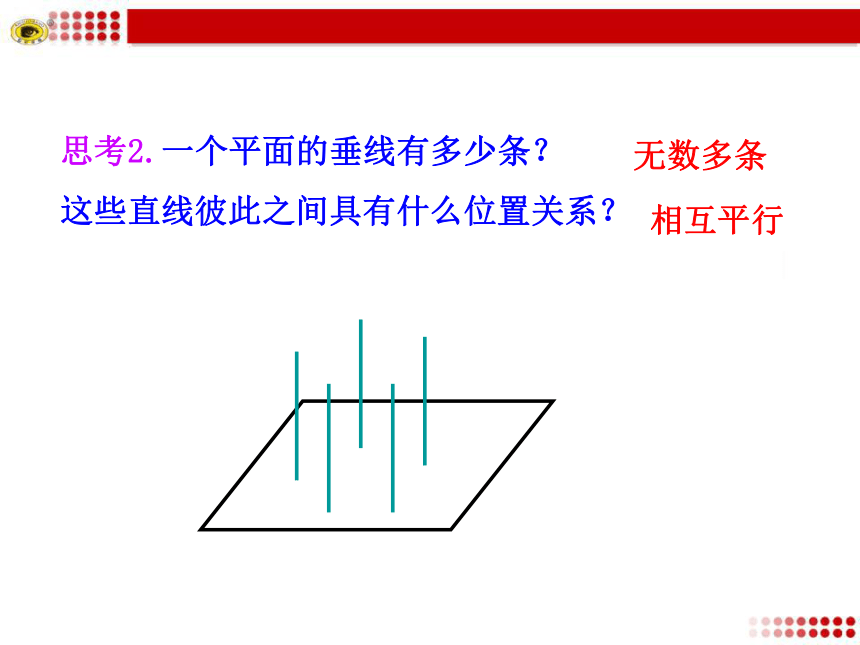
2.能够灵活地应用线面垂直的性质定理证明有关问题.(难点)思考1.如图,长方体ABCD-A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?这些直线都与底面垂直这些直线相互平行思考2.一个平面的垂线有多少条?
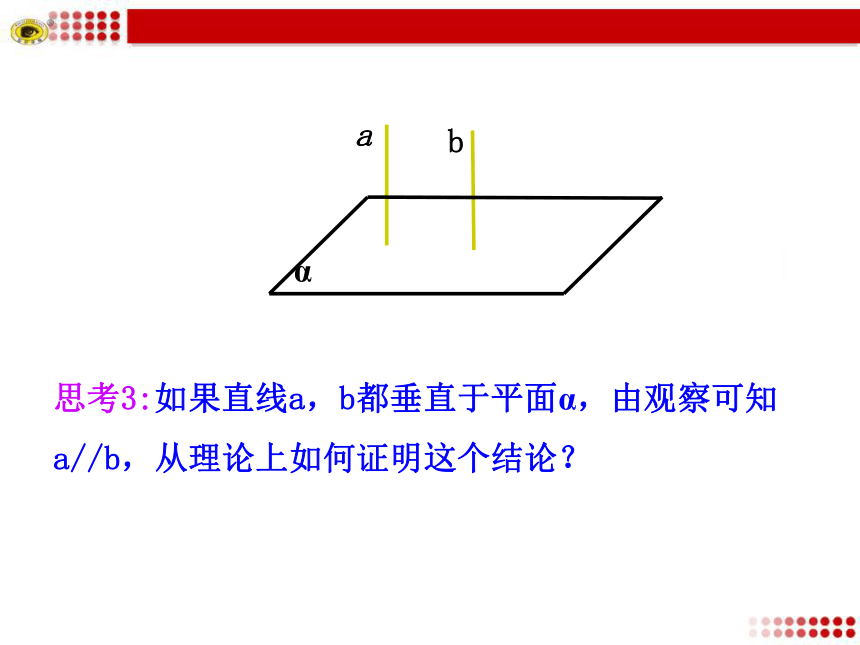
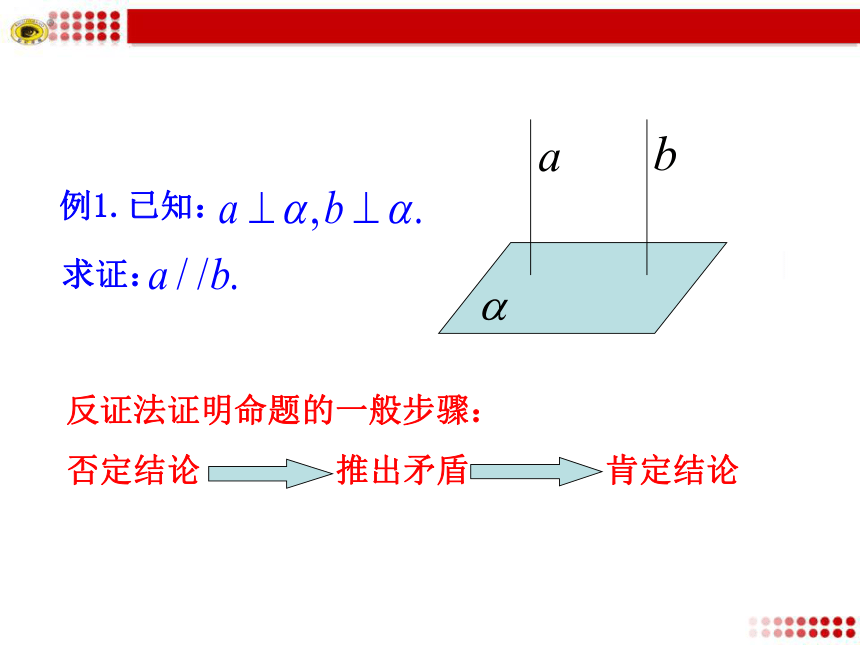
这些直线彼此之间具有什么位置关系?无数多条相互平行思考3:如果直线a,b都垂直于平面α,由观察可知a//b,从理论上如何证明这个结论?例1.已知:求证:经过同一点 的两直线 , 都垂直于 是不可能的,所以证明:
假设 不平行,
设 ,经过点
作直线 与直线 平行假设结论不成立找出矛盾直线与平面垂直的性质定理定理6.3 如果两条直线同垂直于一个平面,那么这两条直线平行. 用符号语言可表述为:思考交流
1.设a,b为直线,α为平面,若a⊥α,b//a,则b与α的位置关系如何?垂直2.设l为直线,α,β为平面,若l⊥α,α//β,则l与β的位置关系如何?垂直3.设l为直线,α,β为平面,若l⊥α,l⊥β,则平面α,β的位置关系如何?平行1.直线l与平面α不垂直,l∩α=O,P∈l,PA⊥α垂
足为A,直线a∥α且a⊥OA,则a与l( )
A.必相交 B.必为异面直线
C.垂直 D.无法确定C2.(2014·辽宁高考)已知m、n表示两条不同的直
线, α表示平面,下列说法正确的是 ( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n?α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥αB3.设l是直线,α,β是两个不同的平面( )
A.若l∥α,l∥β,则α∥β
B.若l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β
D.若α⊥β, l∥α,则l⊥βB提示:若l∥α,l∥β,则α,β可能相交,故A错;
若l∥α,则平面α内必存在一直线m与l平行,又l⊥β,则m⊥β,又m ?α,故α⊥β,故B对;若α⊥β,l⊥α,则l∥β或l ?β,故C错;若α⊥β,l∥α,则l与β关系不确定,故D错.5. 直三棱柱ABC- A1B1C1中,AB=AA1,∠CAB=90°,
证明:CB1⊥BA1.【证明】连接AB1,因为ABC-A1B1C1是直棱柱,∠CAB=90°,所以AC⊥平面ABB1A1,
故AC⊥BA1.
又AB=AA1,则四边形ABB1A1是正方形.
所以BA1⊥AB1,又CA∩AB1=A,
所以,BA1⊥平面CAB1,故CB1⊥BA1.2.转化思想:1.直线和平面垂直的性质定理:
一种证明直线和直线平行的方法;
欲证线线平行,考虑证这两线与某一平面垂直. 不论做什么事,相信自己,别让别人的一句话将你击倒.
第1课时 直线与平面垂直的性质前面我们学习了:
1.直线与平面垂直的定义;
判定直线与平面垂直的方法.
2.直线与平面垂直的判定定理,解决了直线与平面垂直的问题;反之,在直线与平面垂直的条件下,能得到哪些结论?图中立柱与地面是垂直的,你能得出什么结论?立柱相互平行国旗杆与地面都是垂直的,你能发现什么现象?旗杆互相平行1.理解直线与平面垂直的性质定理,并能用文字、符号和图形语言描述定理. (重点)
2.能够灵活地应用线面垂直的性质定理证明有关问题.(难点)思考1.如图,长方体ABCD-A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?这些直线都与底面垂直这些直线相互平行思考2.一个平面的垂线有多少条?
这些直线彼此之间具有什么位置关系?无数多条相互平行思考3:如果直线a,b都垂直于平面α,由观察可知a//b,从理论上如何证明这个结论?例1.已知:求证:经过同一点 的两直线 , 都垂直于 是不可能的,所以证明:
假设 不平行,
设 ,经过点
作直线 与直线 平行假设结论不成立找出矛盾直线与平面垂直的性质定理定理6.3 如果两条直线同垂直于一个平面,那么这两条直线平行. 用符号语言可表述为:思考交流
1.设a,b为直线,α为平面,若a⊥α,b//a,则b与α的位置关系如何?垂直2.设l为直线,α,β为平面,若l⊥α,α//β,则l与β的位置关系如何?垂直3.设l为直线,α,β为平面,若l⊥α,l⊥β,则平面α,β的位置关系如何?平行1.直线l与平面α不垂直,l∩α=O,P∈l,PA⊥α垂
足为A,直线a∥α且a⊥OA,则a与l( )
A.必相交 B.必为异面直线
C.垂直 D.无法确定C2.(2014·辽宁高考)已知m、n表示两条不同的直
线, α表示平面,下列说法正确的是 ( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n?α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥αB3.设l是直线,α,β是两个不同的平面( )
A.若l∥α,l∥β,则α∥β
B.若l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β
D.若α⊥β, l∥α,则l⊥βB提示:若l∥α,l∥β,则α,β可能相交,故A错;
若l∥α,则平面α内必存在一直线m与l平行,又l⊥β,则m⊥β,又m ?α,故α⊥β,故B对;若α⊥β,l⊥α,则l∥β或l ?β,故C错;若α⊥β,l∥α,则l与β关系不确定,故D错.5. 直三棱柱ABC- A1B1C1中,AB=AA1,∠CAB=90°,
证明:CB1⊥BA1.【证明】连接AB1,因为ABC-A1B1C1是直棱柱,∠CAB=90°,所以AC⊥平面ABB1A1,
故AC⊥BA1.
又AB=AA1,则四边形ABB1A1是正方形.
所以BA1⊥AB1,又CA∩AB1=A,
所以,BA1⊥平面CAB1,故CB1⊥BA1.2.转化思想:1.直线和平面垂直的性质定理:
一种证明直线和直线平行的方法;
欲证线线平行,考虑证这两线与某一平面垂直. 不论做什么事,相信自己,别让别人的一句话将你击倒.
同课章节目录
