7.3 球

课件39张PPT。7.3 球 如果用油漆去涂一个乒乓球和一个篮球，且涂的油漆厚度相同，问哪一个球所用的油漆多？为什么？只需要求出它们的表面积 一个充满空气的足球和一个充满空气的篮球，球内的气压相同，若忽略球内部材料的厚度，则哪一个球充入的气体较多？为什么？只需求出它们的体积那如何求球的表面积和体积呢？请进入本节课的学习！1.理解球的截面，并能解决相应问题；
2.了解圆的切线的相关概念；
3.记住球的表面积和体积公式.（重点）
4.会用球的表面积和体积公式进行有关的计算，并能解决一些简单的实际问题.(难点）问题2：把直线换成平面，圆换成球，即用一个平面去截球，情况又怎样呢？提示：圆面.探究点1 球的截面问题1：一条直线与圆相交，在圆内的部分是什么图形？
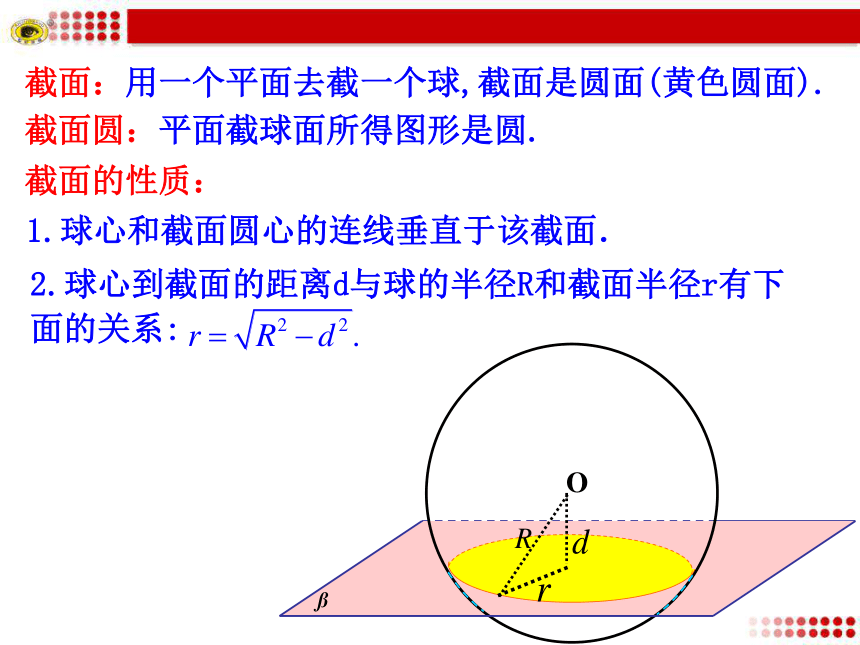
提示：弦（线段）.2.球心到截面的距离d与球的半径R和截面半径r有下面的关系:1.球心和截面圆心的连线垂直于该截面．截面：用一个平面去截一个球,截面是圆面(黄色圆面).
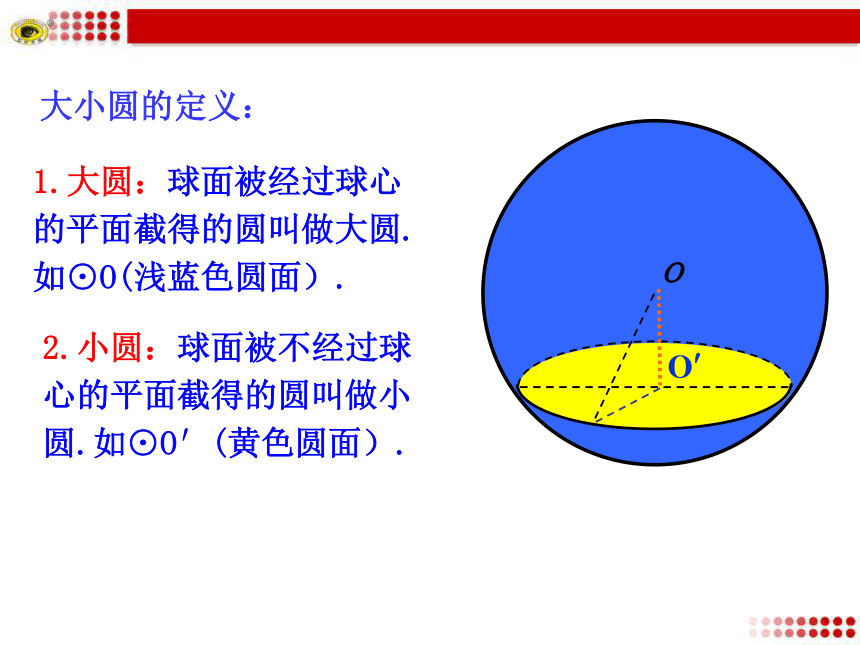
截面圆：平面截球面所得图形是圆. 截面的性质：大小圆的定义： 1.大圆：球面被经过球心的平面截得的圆叫做大圆.如⊙O(浅蓝色圆面）.o2.小圆：球面被不经过球心的平面截得的圆叫做小圆.如⊙O′(黄色圆面）. 问题：在球中，球心到截面的距离d与截面圆的大小
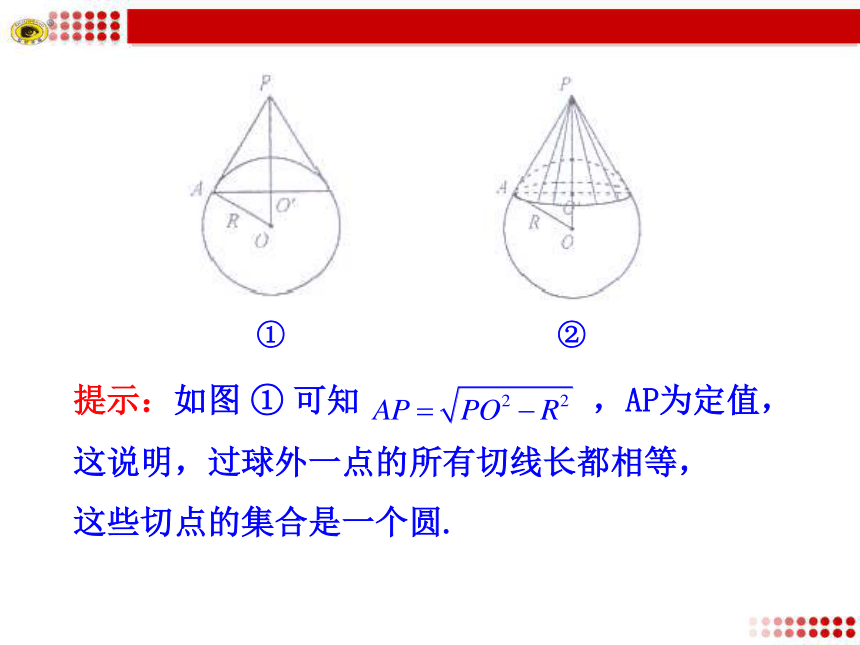
有什么关系？探究点2 球的切线 直线与球相切：当直线与球有唯一交点时，称直线与球相切，其中它们的交点称为直线与球的切点.问题：过球外一点P，有无数条切线，那么所有切线长都相等吗？所有切点组成什么图形？①②提示：如图 ① 可知 ，AP为定值，
这说明，过球外一点的所有切线长都相等，
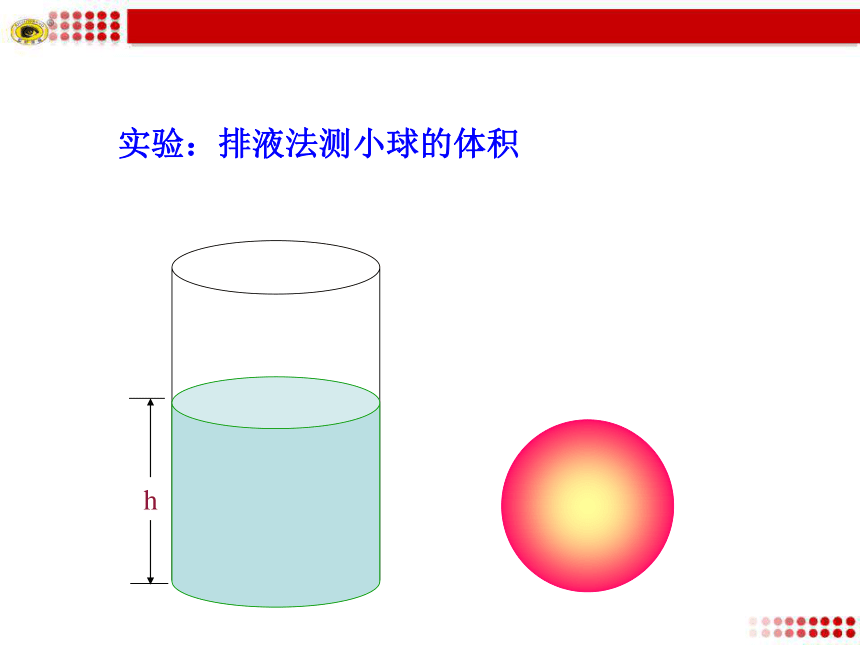
这些切点的集合是一个圆.怎样求球的体积?知识探究探究点3 球的表面积和体积实验：排液法测小球的体积实验：排液法测小球的体积实验：排液法测小球的体积实验：排液法测小球的体积实验：排液法测小球的体积实验：排液法测小球的体积实验：排液法测小球的体积H小球的体积 等于它排开液体的体积实验：排液法测小球的体积割圆术 早在公元三世纪，我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”.他用加倍的方式不断增加圆内接正多边形的边数，使其面积与圆的面积之差更小，即所谓“割之弥细，所失弥小”.这样重复下去，就达到了“割之又割，以至于不可再割，则与圆合体而无所失矣”.这是世界上最早的“极限”思想.球体由N个这样的形状组成球体的分割这样可以求出球体体积为球面被分割成n个网格，表面积分别为：则球的表面积：球的表面积球的表面积是大圆面积的4倍半径是 的球的表面积：观察球的体积与表面积公式，思考下列问题：
思考1:计算球的表面积与体积，关键需要确定哪个量？
提示：要计算球的表面积与体积，关键需要确定球的半径R. 思考2.想一想若球的表面积为S，如何用S表示球的体积V呢？
提示：因为S=4πR2，所以
即球的体积V与表面积S的关系式为思考3.若两球的半径之比为R1∶R2，那么两球的表
面积之比及体积之比分别是多少？
提示：
所以两球的表面积之比为 两球的体积之比
为例1.如图，一个圆锥形的空杯子上面放着一个半球形的冰激凌，如果冰激凌融化了，会溢出杯子吗？（假设冰激凌融化前后体积不变）解： 圆锥因为所以，冰激凌融化了，不会溢出杯子.V半球7.9 g/cm3），每个钢球重145 kg，并且外径等于
50 cm，试根据以上数据，判断钢球是实心的还是空心的．如果是空心的，请你计算出它的内径（π取3.14，结果精确到1 cm）．解：设球的内径是2xcm，那么球的质量为： 答：钢球是空心的,其内径约为45 cm．1.填空
(1)球的表面积变为原来的2倍,则半径变为原来的 倍.
(2)球半径变为原来的2倍，则表面积变为原来的 倍.
(3)两球表面积之比为1︰2，则其体积之比是 .
(4)两球体积之比是1︰2，则其表面积之比是 .注意:影响球的表面积及体积的只有一个元素，就是球的半径. 2. 某几何体的三视图如图所示,它的体积为( )
A. B. C. D.C【解析】选C.该几何体下部分是半径为3,高为4
的圆锥,体积为 ,上部分是半
球,体积为 ,所以体积为 . A球的体积和表面积公式
已知：球的半径为R.
结论：体积V=______，
表面积S=______. 4πR2 不论你在什么时候开始，重要的是开始之后就不要停止.不论你在什么时候结束，重要的是结束之后就不要悔恨.