1.5 第1课时 两点间的距离公式
文档属性
| 名称 | 1.5 第1课时 两点间的距离公式 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 12:24:51 | ||
图片预览






文档简介
课件22张PPT。1.5 平面直角坐标系中的距离公式
第1课时 两点间的距离公式 在初中,我们已经学过数轴上两点间的距离公式;如果把这个问题拓展到平面直角坐标系内又如何来求两点间的距离呢?(x1,y2)1.掌握两点间距离公式的推导过程. (重点)
2.会利用两点间的距离公式解决简单的几何问题.
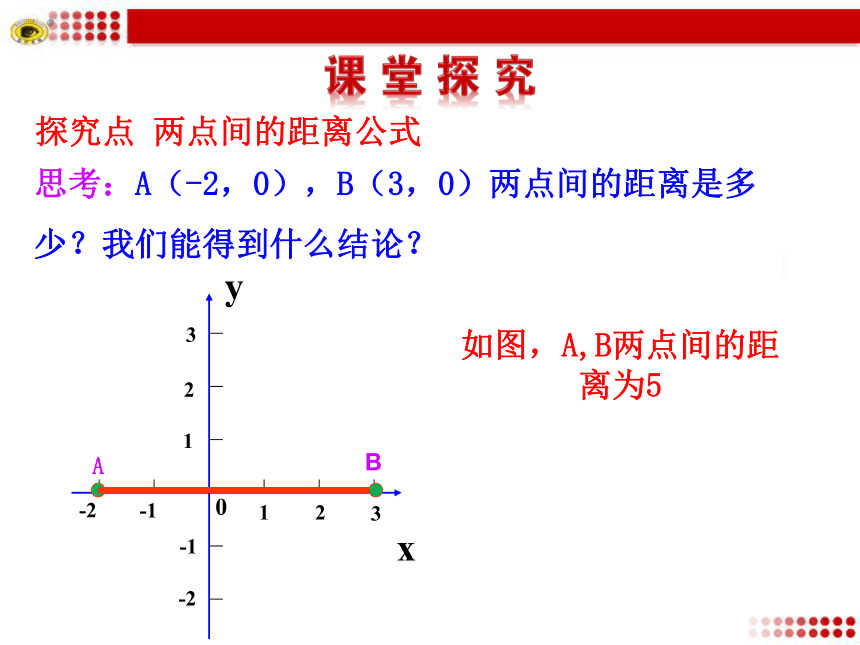
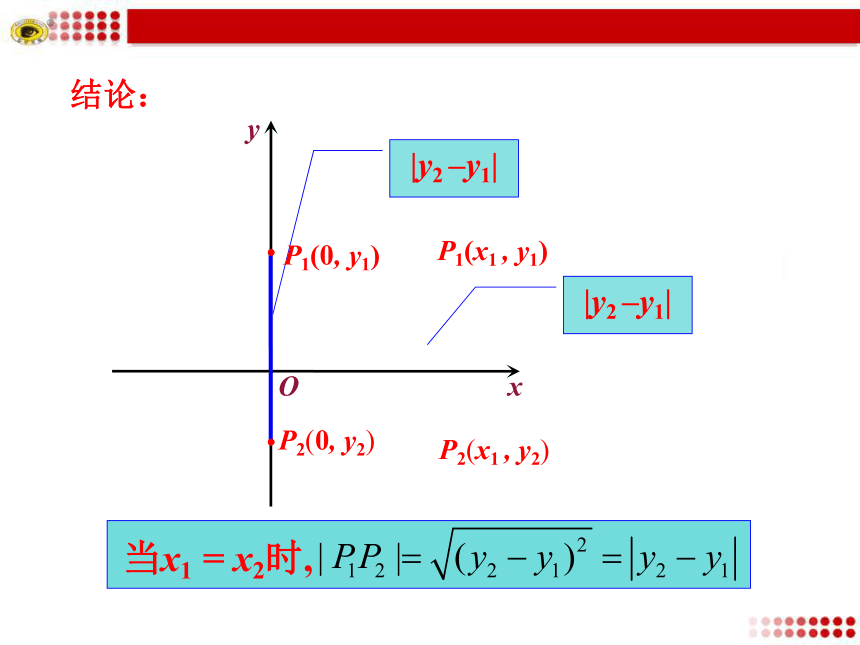
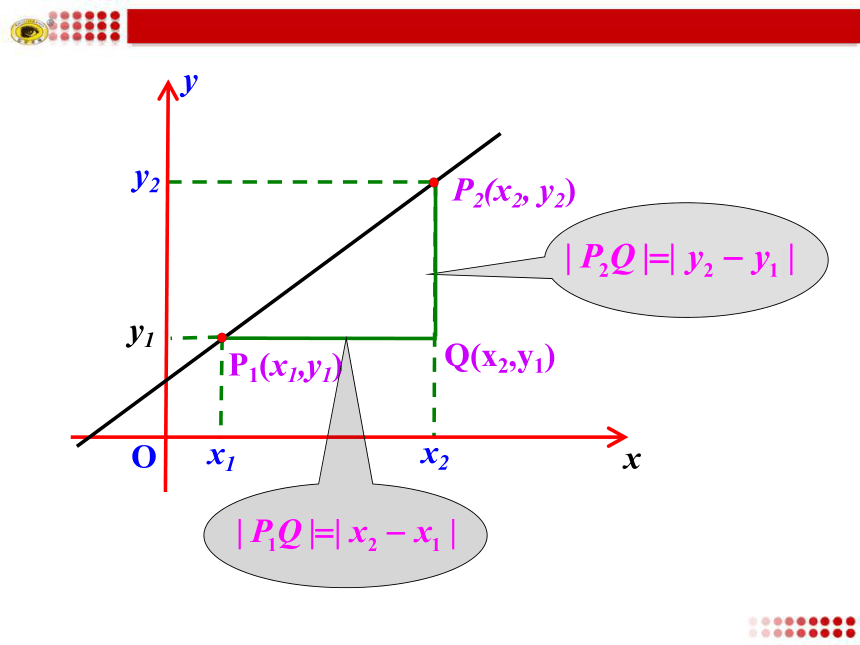
(难点)思考:A(-2,0),B(3,0)两点间的距离是多少?我们能得到什么结论?AB如图,A,B两点间的距离为53探究点 两点间的距离公式P2(x2 , 0)P1(x1 , y)P2(x2 , y)|x2 –x1||x2 –x1|P1(x1 , 0)结论:思考:A(0,2),B(0,-2)两点间的距离是多少?我们能得到什么结论?如图,A,B两点间的距离为4P2(0, y2)P1(x1 , y1)P2(x1 , y2)|y2 –y1|P1(0, y1)|y2 –y1|结论:思考:已知平面上两点P1(x1,y1)和P2(x2,y2),如何求点P1和P2的距离|P1P2|?xyP1(x1,y1)P2(x2,y2)OxyP1(x1,y1)P2(x2, y2)Q(x2,y1)Ox2y2x1y1当y1=y2时,当x1=x2时,试求:P1,P2两点间的距离.两点间距离公式特别地,点A(x,y)到原点(0,0)的距离为 一般地,若两点A,B的坐标分别为(x1,y1), (x2,y2),则A,B两点间的距离公式为(1) (2) 例1 求下列两点间的距离:解:直接利用公式【变式练习】A(-1,0)B(1,0)根据边的关系判断.···【变式练习】根据图形特点,建立适当的直角坐标系,利用坐标解决有关问题,这种方法叫坐标法也称为解析法. 用“坐标法”解决有关几何问题的基本步骤:第一步:建立坐标系,
用坐标系表示有关的量第二步:进行
有关代数运算第三步:把代数运算结果
“翻译”成几何关系【提升总结】1.已知点A(-2,-1),B(a,3)且AB=5,则a的值
是( )
A.1 B.-5 C.1或-5 D.-1或5C2.已知点M(-1,3),N(5,1),点P(x,y)到M,N
的距离相等,则点P(x,y)所满足的方程是( )
A.x+3y-8=0 B.3x-y-4=0
C.x-3y+9=0 D.x-3y+8=0B|AB|=9|AB|=8|AB|=5解:|AB|=5,|BC|= ,|AC|= ,
满足|AB|2=|AC|2+|BC|2,所以 是直角三角形.1.x轴上A,B两点间的距离公式2.平面直角坐标系中,A(x1,y1),B(x2,y2)两点间的距离公式不同的品格导致不同的兴趣爱好.
第1课时 两点间的距离公式 在初中,我们已经学过数轴上两点间的距离公式;如果把这个问题拓展到平面直角坐标系内又如何来求两点间的距离呢?(x1,y2)1.掌握两点间距离公式的推导过程. (重点)
2.会利用两点间的距离公式解决简单的几何问题.
(难点)思考:A(-2,0),B(3,0)两点间的距离是多少?我们能得到什么结论?AB如图,A,B两点间的距离为53探究点 两点间的距离公式P2(x2 , 0)P1(x1 , y)P2(x2 , y)|x2 –x1||x2 –x1|P1(x1 , 0)结论:思考:A(0,2),B(0,-2)两点间的距离是多少?我们能得到什么结论?如图,A,B两点间的距离为4P2(0, y2)P1(x1 , y1)P2(x1 , y2)|y2 –y1|P1(0, y1)|y2 –y1|结论:思考:已知平面上两点P1(x1,y1)和P2(x2,y2),如何求点P1和P2的距离|P1P2|?xyP1(x1,y1)P2(x2,y2)OxyP1(x1,y1)P2(x2, y2)Q(x2,y1)Ox2y2x1y1当y1=y2时,当x1=x2时,试求:P1,P2两点间的距离.两点间距离公式特别地,点A(x,y)到原点(0,0)的距离为 一般地,若两点A,B的坐标分别为(x1,y1), (x2,y2),则A,B两点间的距离公式为(1) (2) 例1 求下列两点间的距离:解:直接利用公式【变式练习】A(-1,0)B(1,0)根据边的关系判断.···【变式练习】根据图形特点,建立适当的直角坐标系,利用坐标解决有关问题,这种方法叫坐标法也称为解析法. 用“坐标法”解决有关几何问题的基本步骤:第一步:建立坐标系,
用坐标系表示有关的量第二步:进行
有关代数运算第三步:把代数运算结果
“翻译”成几何关系【提升总结】1.已知点A(-2,-1),B(a,3)且AB=5,则a的值
是( )
A.1 B.-5 C.1或-5 D.-1或5C2.已知点M(-1,3),N(5,1),点P(x,y)到M,N
的距离相等,则点P(x,y)所满足的方程是( )
A.x+3y-8=0 B.3x-y-4=0
C.x-3y+9=0 D.x-3y+8=0B|AB|=9|AB|=8|AB|=5解:|AB|=5,|BC|= ,|AC|= ,
满足|AB|2=|AC|2+|BC|2,所以 是直角三角形.1.x轴上A,B两点间的距离公式2.平面直角坐标系中,A(x1,y1),B(x2,y2)两点间的距离公式不同的品格导致不同的兴趣爱好.
同课章节目录
