1.5 第2课时 点到直线的距离公式
文档属性
| 名称 | 1.5 第2课时 点到直线的距离公式 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 12:25:04 | ||
图片预览




文档简介
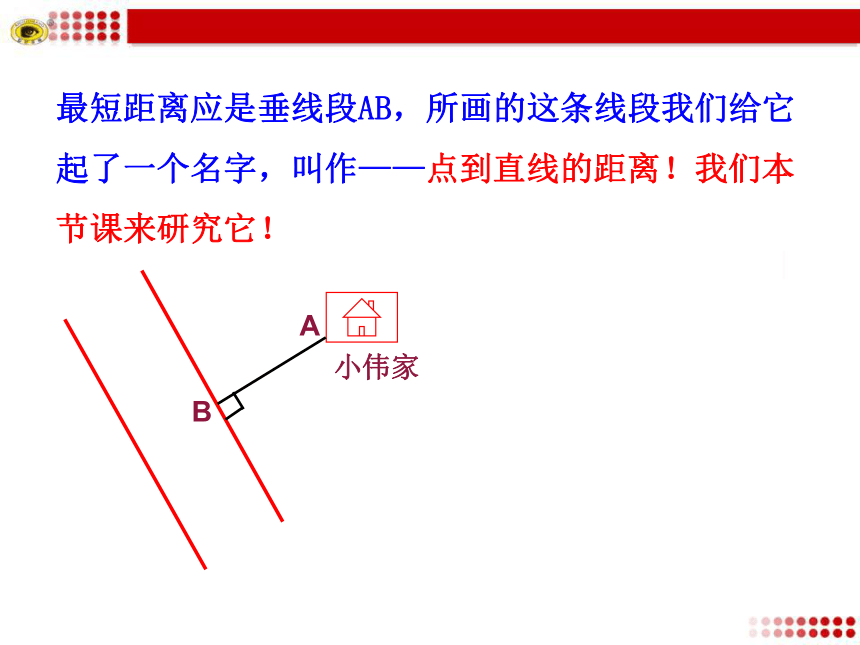
课件29张PPT。第2课时 点到直线的距离公式 小伟家住在公路的一侧,最近他爸爸买了一辆轿车,他家为了方便准备修一条水泥路和公路连接,请问怎样修才能使他家距离公路最近,请画出所修的路线.你认为哪种方案最节省材料?你的理由是什么?最短距离应是垂线段AB,所画的这条线段我们给它起了一个名字,叫作——点到直线的距离!我们本节课来研究它!AB1.知道点到直线的距离公式的推导过程. (重点)
2.会利用点到直线的距离公式求点到直线的距离.
(难点)
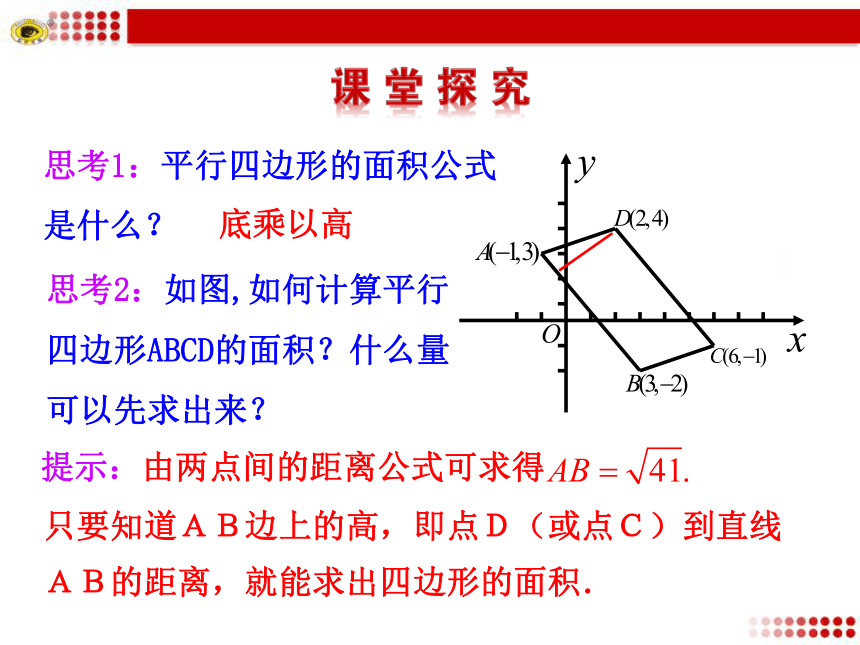
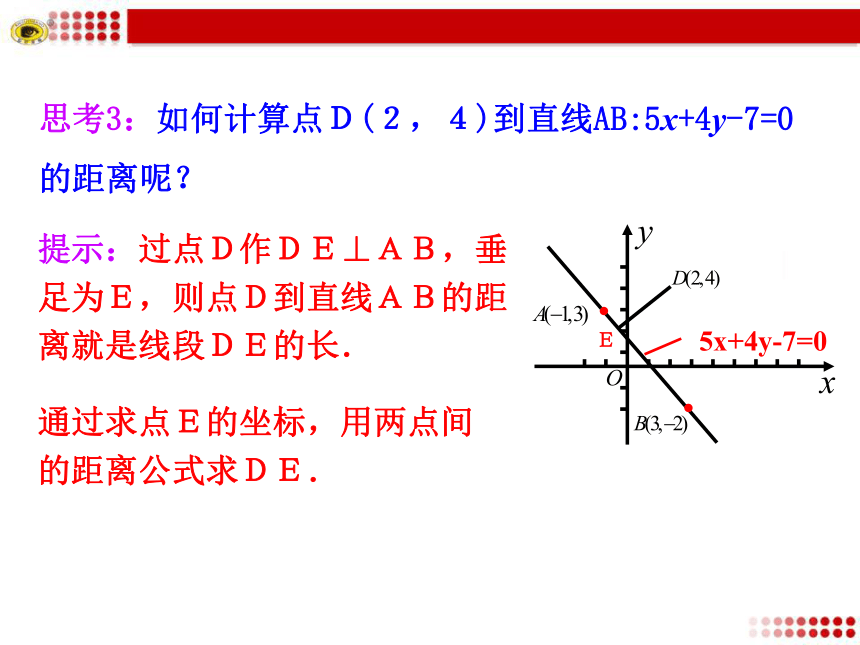
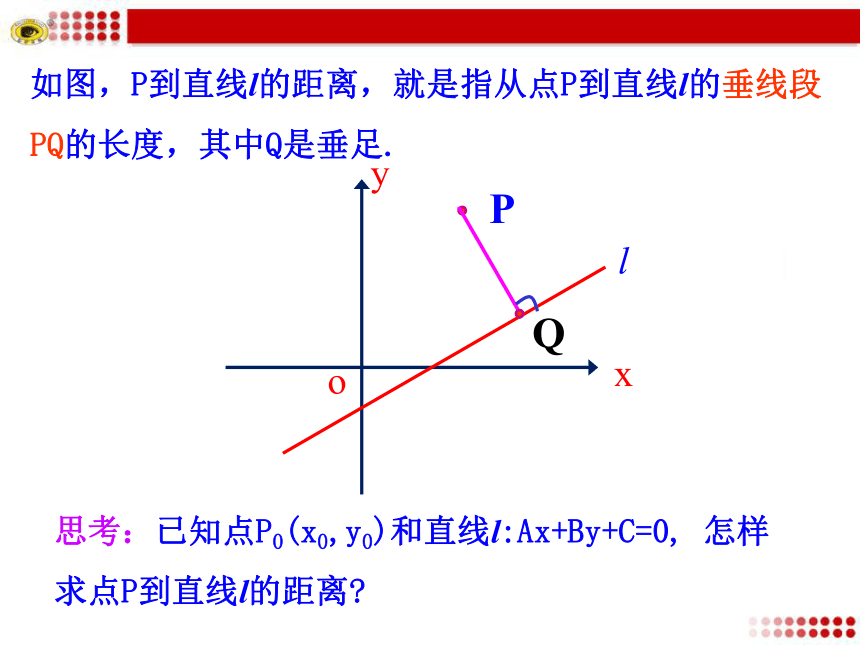
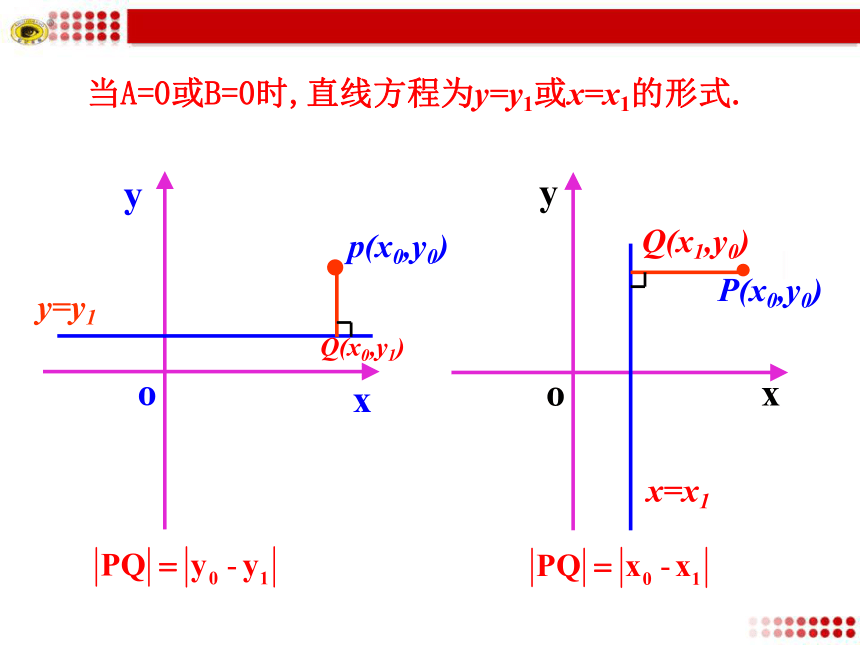
3.会求两条平行直线之间的距离.思考1:平行四边形的面积公式是什么?思考2:如图,如何计算平行四边形ABCD的面积?什么量可以先求出来?底乘以高提示:由两点间的距离公式可求得只要知道AB边上的高,即点D(或点C)到直线AB的距离,就能求出四边形的面积.思考3:如何计算点D(2,4)到直线AB:5x+4y-7=0的距离呢?提示:过点D作DE⊥AB,垂足为E,则点D到直线AB的距离就是线段DE的长.通过求点E的坐标,用两点间的距离公式求DE.E5x+4y-7=04.用两点间的距离公式,求出点D到AB的距离1.由DE⊥AB,可知DE所在直线的斜率为2.求出DE的方程即4x-5y+12=0.3.由AB和DE所在直线的方程得垂足E的坐标Q思考:已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离?如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足. 当A=0或B=0时,直线方程为y=y1或x=x1的形式.Q(x0,y1)Q(x1,y0)点P(-1,2)到直线3x=2的距离是______.
(2)点P(-1,2)到直线3y=2的距离是______.练一练点 之间的距离 ( 到 的距离)xyO下面设A≠0,B ≠0, 我们进一步探求点到直线的距离公式:思路1: 若直线不平行于坐标轴(即A ≠0且B≠0),由 可得它的斜率是直线PQ的方程是与联立,解得一般地,对于直线思路2:三角形的面积公式·PQ是RtΔPMN斜边上的高,由三角形面积可知由此我们得到,的距离点到直线的距离公式点 到直线直线方程为一般式例1.(1)求原点到直线l1:5x-12y-9=0的距离;(2)求点P(-1,2)到直线l2:2x+y-10=0的距离.分析:根据点到直线的距离公式求解.解: (1)原点到直线l1的的距离 (2)点P到直线l2的距离求下列点到直线的距离:
(1)(0,0),3x-2y+4=0 (2)(2,-3),x=y答案: (1) (2) 【变式练习】例2.用解析法证明:等腰三角形底边延长线上一点到两腰的距离之差等于一腰上的高.证明:在△ABC中,AB=AC,P为BC延长线上一点,PD⊥AB于D,PE⊥AC于E,CF⊥AB于F.以BC所在直线为x轴,以BC的中垂线为y轴,建立直角坐标系如图.设A(0,b),B(-a,0),C(a,0)(a>0,b>0),则直线AB方程为bx-ay+ab=0,直线AC方程为bx+ay-ab=0,取P(x0,0),使x0>a,则点P到直线AB,AC的距离分别为则点C到直线AB的距离为则由线到线的距离点到线的距离分析:一般地,已知两条平行直线则即注意:两条直线的未知量的系数相同才能使用上式.思考:直角坐标系中两条平行直线的距离如何求呢?【变式练习】
求下列两条平行直线的距离:
(1) 3x-2y-1=0,3x-2y+6=0
(2) x+2y=0,2x+4y-7=0解析:(1)1.若直线3x+4y-3=0与直线6x+my+2=0平行,则它们
之间的距离为( )A.1B.D.A.2x+y=0 B.2x+y-2=0
C.2x+y=0或2x+y+2=0 D. 2x+y=0或2x+y-2=0 C.D2.与直线2x+y+1=0平行且距离等于 的直线方程
为( )C3.求点(-1,3)到直线3x+4y-5=0的距离.4.求两条平行直线3x+4y-1=0与3x+4y-6=0之间的距离.5.已知点P(2,-1),求下列问题:
(1)过点P且与原点距离为2的直线的方程.
(2)过点P且与原点距离最大的直线l的方程,最大距离是多少?
(3)是否存在过点P且与原点距离为6的直线的方程?若存在,求出方程;若不存在,请说明理由.平面内的几种距离公式小结平面上
的距离两点间的距离点到直线的距离两条平行线间的距离 不是拥有幸福的人才幸福,而是知道幸福的人才幸福.幸福不在于享受了多少,而在于感受了多少.
2.会利用点到直线的距离公式求点到直线的距离.
(难点)
3.会求两条平行直线之间的距离.思考1:平行四边形的面积公式是什么?思考2:如图,如何计算平行四边形ABCD的面积?什么量可以先求出来?底乘以高提示:由两点间的距离公式可求得只要知道AB边上的高,即点D(或点C)到直线AB的距离,就能求出四边形的面积.思考3:如何计算点D(2,4)到直线AB:5x+4y-7=0的距离呢?提示:过点D作DE⊥AB,垂足为E,则点D到直线AB的距离就是线段DE的长.通过求点E的坐标,用两点间的距离公式求DE.E5x+4y-7=04.用两点间的距离公式,求出点D到AB的距离1.由DE⊥AB,可知DE所在直线的斜率为2.求出DE的方程即4x-5y+12=0.3.由AB和DE所在直线的方程得垂足E的坐标Q思考:已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离?如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足. 当A=0或B=0时,直线方程为y=y1或x=x1的形式.Q(x0,y1)Q(x1,y0)点P(-1,2)到直线3x=2的距离是______.
(2)点P(-1,2)到直线3y=2的距离是______.练一练点 之间的距离 ( 到 的距离)xyO下面设A≠0,B ≠0, 我们进一步探求点到直线的距离公式:思路1: 若直线不平行于坐标轴(即A ≠0且B≠0),由 可得它的斜率是直线PQ的方程是与联立,解得一般地,对于直线思路2:三角形的面积公式·PQ是RtΔPMN斜边上的高,由三角形面积可知由此我们得到,的距离点到直线的距离公式点 到直线直线方程为一般式例1.(1)求原点到直线l1:5x-12y-9=0的距离;(2)求点P(-1,2)到直线l2:2x+y-10=0的距离.分析:根据点到直线的距离公式求解.解: (1)原点到直线l1的的距离 (2)点P到直线l2的距离求下列点到直线的距离:
(1)(0,0),3x-2y+4=0 (2)(2,-3),x=y答案: (1) (2) 【变式练习】例2.用解析法证明:等腰三角形底边延长线上一点到两腰的距离之差等于一腰上的高.证明:在△ABC中,AB=AC,P为BC延长线上一点,PD⊥AB于D,PE⊥AC于E,CF⊥AB于F.以BC所在直线为x轴,以BC的中垂线为y轴,建立直角坐标系如图.设A(0,b),B(-a,0),C(a,0)(a>0,b>0),则直线AB方程为bx-ay+ab=0,直线AC方程为bx+ay-ab=0,取P(x0,0),使x0>a,则点P到直线AB,AC的距离分别为则点C到直线AB的距离为则由线到线的距离点到线的距离分析:一般地,已知两条平行直线则即注意:两条直线的未知量的系数相同才能使用上式.思考:直角坐标系中两条平行直线的距离如何求呢?【变式练习】
求下列两条平行直线的距离:
(1) 3x-2y-1=0,3x-2y+6=0
(2) x+2y=0,2x+4y-7=0解析:(1)1.若直线3x+4y-3=0与直线6x+my+2=0平行,则它们
之间的距离为( )A.1B.D.A.2x+y=0 B.2x+y-2=0
C.2x+y=0或2x+y+2=0 D. 2x+y=0或2x+y-2=0 C.D2.与直线2x+y+1=0平行且距离等于 的直线方程
为( )C3.求点(-1,3)到直线3x+4y-5=0的距离.4.求两条平行直线3x+4y-1=0与3x+4y-6=0之间的距离.5.已知点P(2,-1),求下列问题:
(1)过点P且与原点距离为2的直线的方程.
(2)过点P且与原点距离最大的直线l的方程,最大距离是多少?
(3)是否存在过点P且与原点距离为6的直线的方程?若存在,求出方程;若不存在,请说明理由.平面内的几种距离公式小结平面上
的距离两点间的距离点到直线的距离两条平行线间的距离 不是拥有幸福的人才幸福,而是知道幸福的人才幸福.幸福不在于享受了多少,而在于感受了多少.
同课章节目录
