2.3 第1课时 直线与圆的位置关系
文档属性
| 名称 | 2.3 第1课时 直线与圆的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 00:00:00 | ||
图片预览









文档简介
课件34张PPT。 2.3 直线与圆、圆与圆的位置关系
第1课时 直线与圆的位置关系请大家仔细观察!实例1一艘轮船在沿直线返回港口的途中,接到气象台的台
风预报:台风中心位于轮船正西70km处,受影响的范
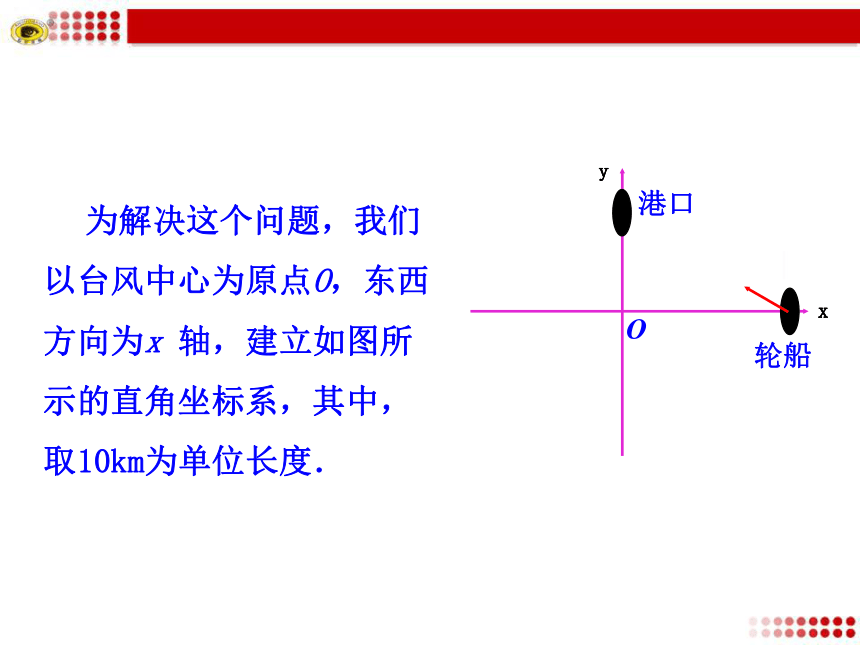
围是半径长为30km的圆形区域.已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?港口实例2:O 为解决这个问题,我们以台风中心为原点O,东西方向为x 轴,建立如图所示的直角坐标系,其中,取10km为单位长度.港口轮船xyxy这样,受台风影响的圆区域所对应的圆心为O 的圆的方程为轮船航线所在直线l的方程为问题归结为:圆心为O 的圆与直线l有无公共点.
本节课我们学习解决它的方法!Oxy1.了解直线与圆的位置关系.(重点)
2. 会用几何法与代数法来判断直线与圆的位置关系.(重点、难点)
3.掌握圆的切线方程的求法及有关弦长问题.(难点)为了大家能看的更清楚些.
以蓝线为水平线,圆圈为太阳!
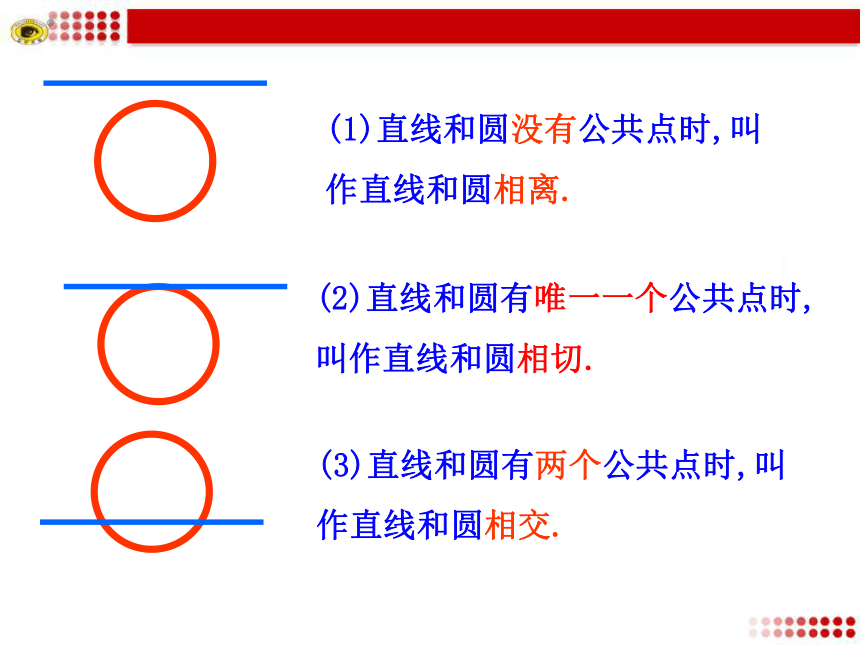
注意观察!!请大家把直线和圆的公共点个数情况总结一下,并把相应的图形画出来.总体看来应该有下列三种情况:(1)直线和圆有一个公共点(2)直线和圆有两个公共点.(3)直线和圆没有公共点.(2)直线和圆有唯一一个公共点时,叫作直线和圆相切.(3)直线和圆有两个公共点时,叫作直线和圆相交.(1)直线和圆没有公共点时,叫作直线和圆相离.大家都知道:点和圆的位置关系可以用圆心到点之间的距离这一数量关系来刻画;那么直线和圆的位置关系是否也可以用数量关系来刻画呢?下面我们一起来研究一下!想一想o圆心O到直线L的距离dL半径r(1)直线L和⊙O相离,此时d与r大小关系为_____.d>r数形结合o圆心O到直线L的距离d半径r(2)直线L和⊙O相切,此时d与r大小关系为______.d=ro圆心O到直线L的距离d半径r(3)直线L和⊙O相交,此时d与r大小关系为_________.dr时,能否得出直线和圆的位置关系为相离?
(2)当d=r时,能否得出直线和圆的位置关系为相切?
(3)当d(d为圆心O到直线L的距离,r为圆O的半径)思考注明:符号” 读作“等价于”.它表示从左端可以推出右端,并且从右端也可以推出左端.几何法判断直线和圆的位置关系直线L和⊙O 相交 d直线L和⊙O 相切 d=r
直线L和⊙O 相离 d>r利用直线与圆的公共点的个数进行判断:直线与圆的位置关系的判断方法【提升总结】已知圆的圆心为C(1,1),半径r=1.(1)点C到直线x-y-2=0的距离为又r=1,所以d1>r,可知直线与圆相离.解:例1.判断下列直线与圆(x-1)2+(y-1)2=1的位置关系:(1)x-y-2=0; (2)x+2y-1=0.判断直线4x-3y-2=0与圆(x-3)2+(y+5)2=36的位置关系.已知圆的圆心为O(3,-5), 半径r=6.点O到直线4x-3y-2=0的距离为又r=6,所以d1﹤r,可知直线与圆相交.解:【变式练习】例2.设直线mx-y+2=0与圆x2+y2=1相切,求实数m的值.已知圆的圆心为O(0,0),半径r=1,则O到已知
直线的距离由已知得d=r,即解:解得利用相切的等价条件【思路探索】利用圆心到直线的距离等于圆的半径求出直线斜率,进而求出切线方程.【变式练习】解:因为(4-3)2+(-3-1)2=17>1,所以点A在圆外.
(1)若所求直线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4).
因为圆心C(3,1)到切线的距离等于半径,半径为1,
所以 =1,即|k+4|= ,
所以k2+8k+16=k2+1.
解得k= .所以切线方程为y+3= (x-4),
即15x+8y-36=0.(2)若直线斜率不存在,
圆心C(3,1)到直线x=4的距离也为1,
这时直线与圆也相切,
所以另一条切线方程是x=4.
综上,所求切线方程为15x+8y-36=0或x=4.1.⊙O的半径为3,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d的取值范围为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和
⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交 AC5.如图,已知直线l: 和圆心为C的圆 ,判断直线l与圆的位置关系;如果相交,求它们交点的坐标.联立
解得:所以,直线 l 与圆有两个交点,它们的坐标分别是:把 代入方程①,得 ;把 代入方程① ,得 . A(2,0),B(1,3)解:判定直线与圆的位置关系的方法有两种
(1)代数方法,由直线与圆的公共点的个数来判断
(2)几何方法,由圆心到直线的距离d与半径r的关系判断.
在实际应用中,常采用第二种方法判定. 不是每一粒种子都能发芽,不是每一段路程都铺满鲜花,不过不要忘记,乌云遮不住太阳的光华.
第1课时 直线与圆的位置关系请大家仔细观察!实例1一艘轮船在沿直线返回港口的途中,接到气象台的台
风预报:台风中心位于轮船正西70km处,受影响的范
围是半径长为30km的圆形区域.已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?港口实例2:O 为解决这个问题,我们以台风中心为原点O,东西方向为x 轴,建立如图所示的直角坐标系,其中,取10km为单位长度.港口轮船xyxy这样,受台风影响的圆区域所对应的圆心为O 的圆的方程为轮船航线所在直线l的方程为问题归结为:圆心为O 的圆与直线l有无公共点.
本节课我们学习解决它的方法!Oxy1.了解直线与圆的位置关系.(重点)
2. 会用几何法与代数法来判断直线与圆的位置关系.(重点、难点)
3.掌握圆的切线方程的求法及有关弦长问题.(难点)为了大家能看的更清楚些.
以蓝线为水平线,圆圈为太阳!
注意观察!!请大家把直线和圆的公共点个数情况总结一下,并把相应的图形画出来.总体看来应该有下列三种情况:(1)直线和圆有一个公共点(2)直线和圆有两个公共点.(3)直线和圆没有公共点.(2)直线和圆有唯一一个公共点时,叫作直线和圆相切.(3)直线和圆有两个公共点时,叫作直线和圆相交.(1)直线和圆没有公共点时,叫作直线和圆相离.大家都知道:点和圆的位置关系可以用圆心到点之间的距离这一数量关系来刻画;那么直线和圆的位置关系是否也可以用数量关系来刻画呢?下面我们一起来研究一下!想一想o圆心O到直线L的距离dL半径r(1)直线L和⊙O相离,此时d与r大小关系为_____.d>r数形结合o圆心O到直线L的距离d半径r(2)直线L和⊙O相切,此时d与r大小关系为______.d=ro圆心O到直线L的距离d半径r(3)直线L和⊙O相交,此时d与r大小关系为_________.d
(2)当d=r时,能否得出直线和圆的位置关系为相切?
(3)当d
直线L和⊙O 相离 d>r利用直线与圆的公共点的个数进行判断:直线与圆的位置关系的判断方法【提升总结】已知圆的圆心为C(1,1),半径r=1.(1)点C到直线x-y-2=0的距离为又r=1,所以d1>r,可知直线与圆相离.解:例1.判断下列直线与圆(x-1)2+(y-1)2=1的位置关系:(1)x-y-2=0; (2)x+2y-1=0.判断直线4x-3y-2=0与圆(x-3)2+(y+5)2=36的位置关系.已知圆的圆心为O(3,-5), 半径r=6.点O到直线4x-3y-2=0的距离为又r=6,所以d1﹤r,可知直线与圆相交.解:【变式练习】例2.设直线mx-y+2=0与圆x2+y2=1相切,求实数m的值.已知圆的圆心为O(0,0),半径r=1,则O到已知
直线的距离由已知得d=r,即解:解得利用相切的等价条件【思路探索】利用圆心到直线的距离等于圆的半径求出直线斜率,进而求出切线方程.【变式练习】解:因为(4-3)2+(-3-1)2=17>1,所以点A在圆外.
(1)若所求直线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4).
因为圆心C(3,1)到切线的距离等于半径,半径为1,
所以 =1,即|k+4|= ,
所以k2+8k+16=k2+1.
解得k= .所以切线方程为y+3= (x-4),
即15x+8y-36=0.(2)若直线斜率不存在,
圆心C(3,1)到直线x=4的距离也为1,
这时直线与圆也相切,
所以另一条切线方程是x=4.
综上,所求切线方程为15x+8y-36=0或x=4.1.⊙O的半径为3,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d的取值范围为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和
⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交 AC5.如图,已知直线l: 和圆心为C的圆 ,判断直线l与圆的位置关系;如果相交,求它们交点的坐标.联立
解得:所以,直线 l 与圆有两个交点,它们的坐标分别是:把 代入方程①,得 ;把 代入方程① ,得 . A(2,0),B(1,3)解:判定直线与圆的位置关系的方法有两种
(1)代数方法,由直线与圆的公共点的个数来判断
(2)几何方法,由圆心到直线的距离d与半径r的关系判断.
在实际应用中,常采用第二种方法判定. 不是每一粒种子都能发芽,不是每一段路程都铺满鲜花,不过不要忘记,乌云遮不住太阳的光华.
同课章节目录
