2.3 第2课时 圆与圆的位置关系
文档属性
| 名称 | 2.3 第2课时 圆与圆的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 12:32:25 | ||
图片预览








文档简介
课件32张PPT。第2课时 圆与圆的位置关系我们为你
骄傲!—北京?奥运你能举出生活中表示两个圆不同位置关系的实例吗?你能找出上图中圆与圆的位置关系吗?1. 理解圆与圆的位置关系的种类. (重点)
2. 会利用几何法判断圆与圆的位置关系. (难点)
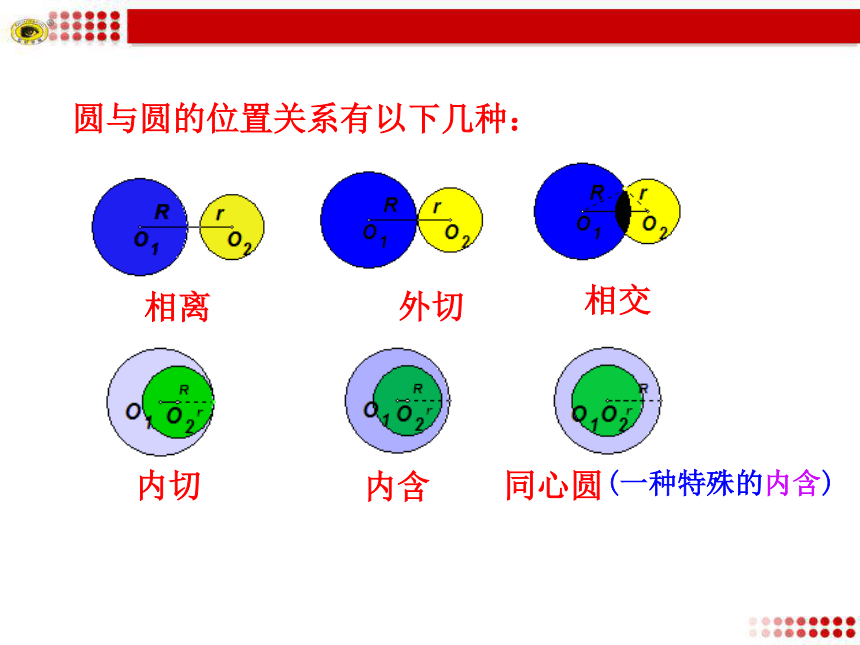
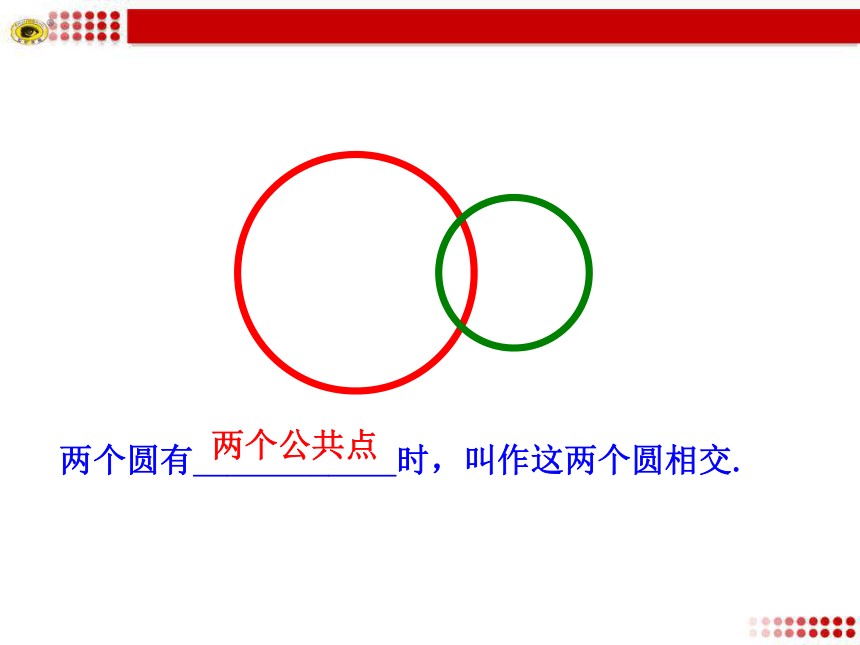
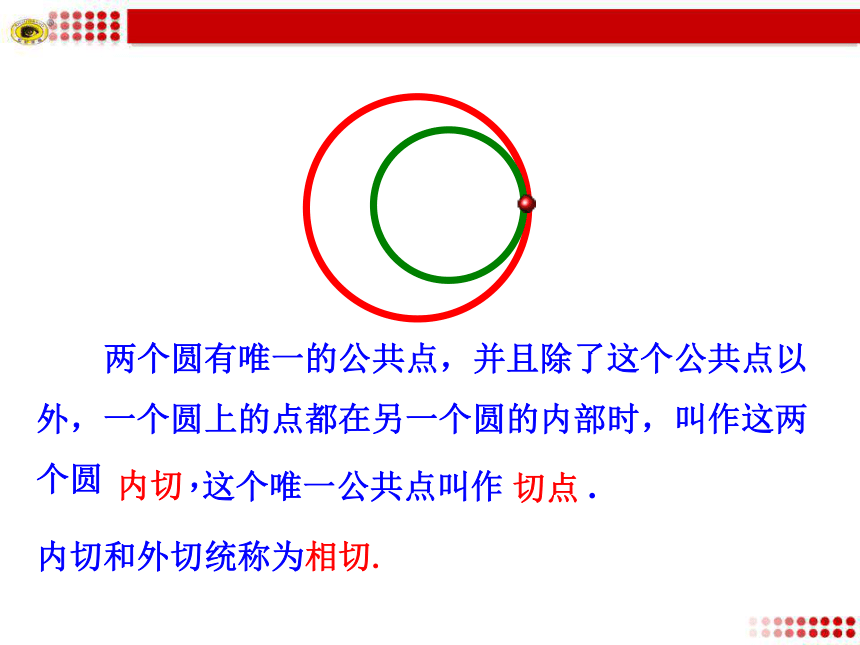
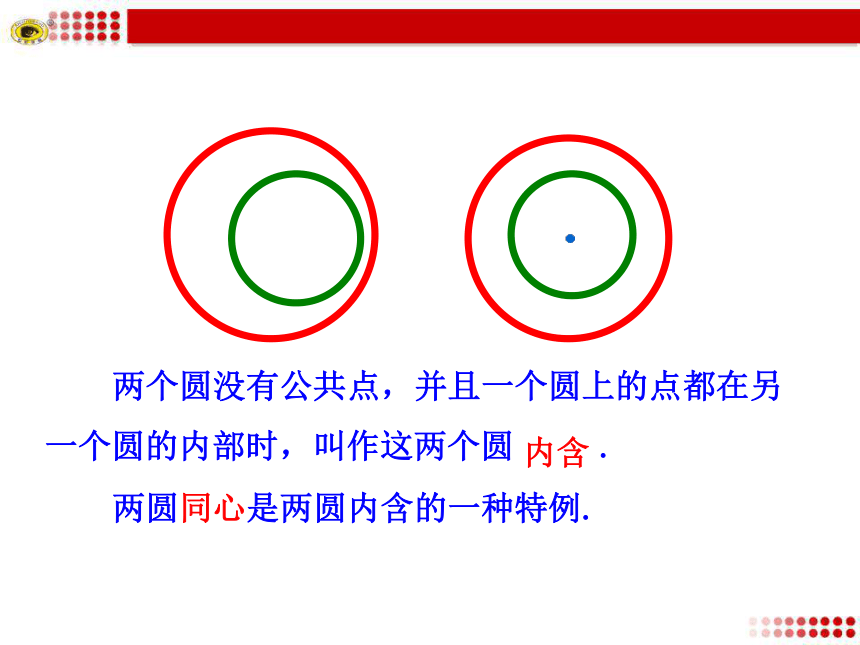
3. 掌握用圆与圆的方程来判断圆与圆的位置关系的方法.思考 圆与圆有几种位置关系?探究点1 圆与圆的位置关系种类提示:相离、外切、相交、内切、内含圆与圆的位置关系有以下几种:相离外切相交内切内含同心圆(一种特殊的内含)两个圆____________,并且每个圆上的点都在另一个圆的外部时,叫作这两个圆相离.没有公共点两个圆有______________,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫作这两个圆外切,这个唯一的公共点叫作切点.唯一的公共点两个圆有____________时,叫作这两个圆相交.两个公共点 两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫作这两个圆 , 内切这个唯一公共点叫作 .切点内切和外切统称为相切. 两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫作这两个圆 .内含 两圆同心是两圆内含的一种特例.O1O2Rrd思考:两圆的位置关系怎样来判断?1.几何方法:两圆相离 d>R+r探究点2 两圆位置关系的判断RrdO1O2T两圆外切 d=R+rO1O2rRd两圆内切 d=R-r (R>r)TOO1O2Rrd两圆内含 dr)O1O2dRr两圆相交 R-rr)注意半径的大小2.代数法判断圆与圆的位置关系 将两个圆的方程联立,消去其中的一个未知数y或x,得关于x或y的一元二次方程.
若方程中Δ>0,则两圆相交;若方程中Δ=0,则两圆相切;若方程中Δ<0,两圆相离或内含.(此方法仅用于判断两个圆的位置关系,不适用于其他的二次曲线的位置关系的判断问题)圆
和
圆
的
位
置
关
系相 离内 切相 交外 切内 含没有公共点一个公共点两个公共点两圆位置关系的判断:几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)【提升总结】判断两圆位置关系几何方法代数方法各有何优劣,如何选用?几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0,Δ<0时,不能判
断两圆的具体位置关系.例1.在平面直角坐标系中分别作出圆心为C1(0,0),
C2(1,1),半径分别为1,2的两圆,并判断两圆的位置关系.两圆半径分别记作r1和r2,则r1=1,r2=2,圆心距于是,解:作出两圆,如图所示.所以两圆相交.判断下列两圆的位置关系:与解:两圆圆心分别为(-2,2)和(2,5),半径分别为r1=1和r2=4,且圆心距: 所以两圆外切.【变式练习】解:由已知得:圆C1:(x+1)2+(y-3)2=36,其圆心C1(-1,3) ,半径r1=6;例2.(1)判断圆C1:x2+y2+2x-6y-26=0与圆C2:x2+y2-4x+2y+4=0的位置关系,并画出图形.(2)判断圆x2+y2-2y=0和圆x2+y2-2 x-6=0的位置关系.解:两圆的方程分别变形为
x2+(y-1)2=12,(x- )2+y2=32.已知:圆C1:x2+y2-2x-3=0;圆C2:x2+y2-4x+2y+3=0;
试判断两圆的位置关系,若有交点,求出交点坐标.解:(1) 变为标准方程:C1:(x-1)2+y2=4;
C2:(x-2)2+(y+1)2=2.圆心坐标分别为(1,0)和(2,-1),
圆心距d= ,半径分别为r1=2, r2= ,这两个圆相交.【变式练习】(2) 将C1和C2的方程联立,消去x2 和y2 项,
化简得:x=y+3,将上式代入C1得:解得:相应地有:x1=3,x2=1.即交点坐标为(3,0)和(1,-2).1.圆x2+y2-2x=0和圆x2+y2+4y=0的位置关系是( )
A.相离 B.外切 C.相交 D.内切CB3.圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系
为( )
A.内切 B.相交 C.外切 D.相离B4. 判断下列各题中两圆的位置关系:
(1)C1:x2+y2+2x-6y-26=0, C2: x2+y2-4x+2y-4=0;
(2)C1:(x+2)2+(y-2)2=13, C2: (x-4)2+(y+2)2=13;
(3)C1:x2+y2=9, C2: (x-2)2+y2=1答案与提示: (1)|r1-r2|=3<|C1C2|所以两圆圆心均在第一象限且横、纵坐标相等.
设两圆的圆心分别为(a,a),(b,b),
则有(4-a)2 +(1-a)2=a2, (4-b)2 +(1-b)2=b2 ,即a,b为方程(4-x)2 +(1-x)2=x2的两个根,
整理得x2-10x +17=0, 所以a+b=10, ab=17,
所以(a-b)2 =(a+b)2-4ab=100-4×17=32,
所以|C1C2|=?
1.圆与圆的位置关系的种类.
2.判定圆与圆的位置关系的两种方法
(1)代数方法,由圆与圆的公共点的个数来判断.
(2)几何方法,由圆心距d与两圆半径的差与和的关系判断.
在实际应用中,常采用第二种方法判定. 不是境况造就人,而是人造就境况.
骄傲!—北京?奥运你能举出生活中表示两个圆不同位置关系的实例吗?你能找出上图中圆与圆的位置关系吗?1. 理解圆与圆的位置关系的种类. (重点)
2. 会利用几何法判断圆与圆的位置关系. (难点)
3. 掌握用圆与圆的方程来判断圆与圆的位置关系的方法.思考 圆与圆有几种位置关系?探究点1 圆与圆的位置关系种类提示:相离、外切、相交、内切、内含圆与圆的位置关系有以下几种:相离外切相交内切内含同心圆(一种特殊的内含)两个圆____________,并且每个圆上的点都在另一个圆的外部时,叫作这两个圆相离.没有公共点两个圆有______________,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫作这两个圆外切,这个唯一的公共点叫作切点.唯一的公共点两个圆有____________时,叫作这两个圆相交.两个公共点 两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫作这两个圆 , 内切这个唯一公共点叫作 .切点内切和外切统称为相切. 两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫作这两个圆 .内含 两圆同心是两圆内含的一种特例.O1O2Rrd思考:两圆的位置关系怎样来判断?1.几何方法:两圆相离 d>R+r探究点2 两圆位置关系的判断RrdO1O2T两圆外切 d=R+rO1O2rRd两圆内切 d=R-r (R>r)TOO1O2Rrd两圆内含 d
若方程中Δ>0,则两圆相交;若方程中Δ=0,则两圆相切;若方程中Δ<0,两圆相离或内含.(此方法仅用于判断两个圆的位置关系,不适用于其他的二次曲线的位置关系的判断问题)圆
和
圆
的
位
置
关
系相 离内 切相 交外 切内 含没有公共点一个公共点两个公共点两圆位置关系的判断:几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)【提升总结】判断两圆位置关系几何方法代数方法各有何优劣,如何选用?几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0,Δ<0时,不能判
断两圆的具体位置关系.例1.在平面直角坐标系中分别作出圆心为C1(0,0),
C2(1,1),半径分别为1,2的两圆,并判断两圆的位置关系.两圆半径分别记作r1和r2,则r1=1,r2=2,圆心距于是,解:作出两圆,如图所示.所以两圆相交.判断下列两圆的位置关系:与解:两圆圆心分别为(-2,2)和(2,5),半径分别为r1=1和r2=4,且圆心距: 所以两圆外切.【变式练习】解:由已知得:圆C1:(x+1)2+(y-3)2=36,其圆心C1(-1,3) ,半径r1=6;例2.(1)判断圆C1:x2+y2+2x-6y-26=0与圆C2:x2+y2-4x+2y+4=0的位置关系,并画出图形.(2)判断圆x2+y2-2y=0和圆x2+y2-2 x-6=0的位置关系.解:两圆的方程分别变形为
x2+(y-1)2=12,(x- )2+y2=32.已知:圆C1:x2+y2-2x-3=0;圆C2:x2+y2-4x+2y+3=0;
试判断两圆的位置关系,若有交点,求出交点坐标.解:(1) 变为标准方程:C1:(x-1)2+y2=4;
C2:(x-2)2+(y+1)2=2.圆心坐标分别为(1,0)和(2,-1),
圆心距d= ,半径分别为r1=2, r2= ,这两个圆相交.【变式练习】(2) 将C1和C2的方程联立,消去x2 和y2 项,
化简得:x=y+3,将上式代入C1得:解得:相应地有:x1=3,x2=1.即交点坐标为(3,0)和(1,-2).1.圆x2+y2-2x=0和圆x2+y2+4y=0的位置关系是( )
A.相离 B.外切 C.相交 D.内切CB3.圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系
为( )
A.内切 B.相交 C.外切 D.相离B4. 判断下列各题中两圆的位置关系:
(1)C1:x2+y2+2x-6y-26=0, C2: x2+y2-4x+2y-4=0;
(2)C1:(x+2)2+(y-2)2=13, C2: (x-4)2+(y+2)2=13;
(3)C1:x2+y2=9, C2: (x-2)2+y2=1答案与提示: (1)|r1-r2|=3<|C1C2|
设两圆的圆心分别为(a,a),(b,b),
则有(4-a)2 +(1-a)2=a2, (4-b)2 +(1-b)2=b2 ,即a,b为方程(4-x)2 +(1-x)2=x2的两个根,
整理得x2-10x +17=0, 所以a+b=10, ab=17,
所以(a-b)2 =(a+b)2-4ab=100-4×17=32,
所以|C1C2|=?
1.圆与圆的位置关系的种类.
2.判定圆与圆的位置关系的两种方法
(1)代数方法,由圆与圆的公共点的个数来判断.
(2)几何方法,由圆心距d与两圆半径的差与和的关系判断.
在实际应用中,常采用第二种方法判定. 不是境况造就人,而是人造就境况.
同课章节目录
