1.4.1 有理数的乘法 第二课时 课件(24张PPT)
文档属性
| 名称 | 1.4.1 有理数的乘法 第二课时 课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 09:18:41 | ||
图片预览








文档简介
(共24张PPT)
第一章
有理数
1.4.1 有理数的乘法
第2课时 有理数乘法的运算律及运用
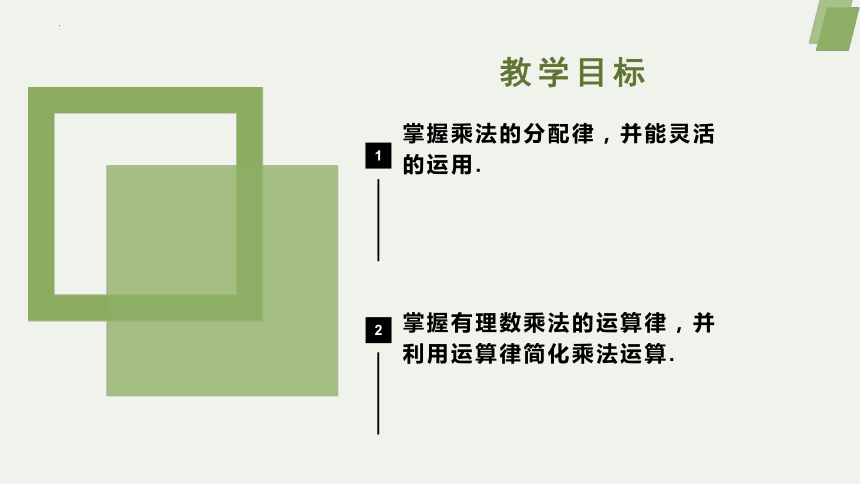
教学目标
掌握乘法的分配律,并能灵活的运用.
掌握有理数乘法的运算律,并利用运算律简化乘法运算.
1
2
复习回顾
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
思考:(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
复习回顾
1.几个非零的数相乘:
几个不是0的数相乘,当负因数的个数是_____时,积是正数;当负因数的个数是_____时,积是负数.
偶数
奇数
2.几个数相乘,其中含有0:
几个数相乘,如果其中有因数为0,那么积等于0.
新知探究
1.小学学习哪些乘法运算律?
2.小学的乘法运算律在有理数乘法成立吗?请举例说明.
新知探究
两个数相乘,交换两个因数的位置,积相等.
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
1.乘法交换律:
2.乘法结合律:
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
3.乘法分配律:
a(b+c)=ab+ac
(ab)c=a(bc).
新知探究
第一组:
(2) (3×4)×0.25= 3×(4×0.25)=
(3) 2×(3+4)= 2×3+2×4=
(1) 2×3= 3×2=
思考:上面每小组运算分别体现了什么运算律?
2×3 3×2
(3×4)×0.25 3×(4×0.25)
2×(3+4) 2×3+2×4
6
6
3
3
14
14
=
=
=
巩固练习
5×(-4) =
15-35=
第二组:
(2) [3×(-4)]×(- 5)=
3×[(-4)×(-5)]=
(3) 5×[3+(-7 )]=
5×3+5×(-7 )=
(1) 5×(-6) = (-6 )×5=
-30
-30
60
60
-20
-20
5× (-6) (-6) ×5
[3×(-4)]×(- 5) 3×[(-4)×(-5)]
5×[3+(-7 )] 5×3+5×(-7 )
=
=
=
(-12)×(-5) =
3×20=
归纳小结
结论:
(1)第一组式子中数的范围是 ________;
(2)第二组式子中数的范围是 ________;
(3)比较第一组和第二组中的算式,可以发现
正数
有理数
各运算律在有理数范围内仍然适用
新知探究
两个数相乘,交换两个因数的位置,积相等.
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
1.乘法交换律:
2.乘法结合律:
数的范围已扩充到有理数.
注意:
用字母表示乘数时,“×”号可以写成“·”或省略,
如a×b可以写成a·b或ab.
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
新知探究
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
a(b+c)
ab+ac
=
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
3.乘法分配律:
巩固练习
1.计算(-3)×2×(-5)=(-3)×[2×(-5)],这是运用了( )
A.乘法交换律
B.乘法结合律
C.乘法分配律
D.乘法交换律、乘法结合律
B
巩固练习
2.用两种方法计算:
思考:可以使用哪两种方法?请你动手做一做.
巩固练习
解:
方法1:
方法2:
巩固练习
3.观察下列计算过程,看其中运用了什么运算律?运算过程是否存在错误?哪里出现了错误?请指正.
巩固练习
正解:
特别提醒:
1. 用分配律时,一定要注意符号不能弄错、弄丢;
2. 括号外一项与括号内每一项都要相乘,不能漏项.
课堂练习
1.三个数相乘积为负数,则其中负因数的个数有( )
A.1个 B.2个
C.3个 D.1个或3个
D
提示:负因数的个数为奇数,积为负数.
课堂练习
2.下面乘积中符号为正的是( )
A.
B.
C.
D.
提示:负因数的个数为偶数,积为正数.
C
课堂练习
3. 口算:
(1)(-2)×3×4×(-1)
(2)(-5)×(-3)×4×(-2)
(3)(-2)×(-2)×(-2)×(-2)
(4)(-3)×(-3)×(-3)×(-3)
=24
=-120
=16
=81
课堂练习
4.计算:
解:(1)原式=(-6)×(-4)= 24
课堂练习
4.计算:
解:(2)原式=
课堂练习
5.若a、b、c为有理数,且|a+1|+|b+2|+|c+3|=0,求(a-1)(b+2)(c-3)的值.
解:∵ |a+1|+|b+2|+|c+3|=0,
∴ a=-1,b=-2,c=-3,
则(a-1)(b+2)(c-3)=0.
课堂总结
有理数乘法运算律
1.乘法交换律:两个数相乘,交换两个因数的位置,积不变.
ab=ba
2.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变. (ab)c=a(bc)
3.乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.a(b+c)=a(b+c)
1.4.1 有理数的乘法
第2课时 有理数乘法的运算律及运用
谢谢观看
有理数
第一章
有理数
1.4.1 有理数的乘法
第2课时 有理数乘法的运算律及运用
教学目标
掌握乘法的分配律,并能灵活的运用.
掌握有理数乘法的运算律,并利用运算律简化乘法运算.
1
2
复习回顾
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
思考:(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
复习回顾
1.几个非零的数相乘:
几个不是0的数相乘,当负因数的个数是_____时,积是正数;当负因数的个数是_____时,积是负数.
偶数
奇数
2.几个数相乘,其中含有0:
几个数相乘,如果其中有因数为0,那么积等于0.
新知探究
1.小学学习哪些乘法运算律?
2.小学的乘法运算律在有理数乘法成立吗?请举例说明.
新知探究
两个数相乘,交换两个因数的位置,积相等.
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
1.乘法交换律:
2.乘法结合律:
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
3.乘法分配律:
a(b+c)=ab+ac
(ab)c=a(bc).
新知探究
第一组:
(2) (3×4)×0.25= 3×(4×0.25)=
(3) 2×(3+4)= 2×3+2×4=
(1) 2×3= 3×2=
思考:上面每小组运算分别体现了什么运算律?
2×3 3×2
(3×4)×0.25 3×(4×0.25)
2×(3+4) 2×3+2×4
6
6
3
3
14
14
=
=
=
巩固练习
5×(-4) =
15-35=
第二组:
(2) [3×(-4)]×(- 5)=
3×[(-4)×(-5)]=
(3) 5×[3+(-7 )]=
5×3+5×(-7 )=
(1) 5×(-6) = (-6 )×5=
-30
-30
60
60
-20
-20
5× (-6) (-6) ×5
[3×(-4)]×(- 5) 3×[(-4)×(-5)]
5×[3+(-7 )] 5×3+5×(-7 )
=
=
=
(-12)×(-5) =
3×20=
归纳小结
结论:
(1)第一组式子中数的范围是 ________;
(2)第二组式子中数的范围是 ________;
(3)比较第一组和第二组中的算式,可以发现
正数
有理数
各运算律在有理数范围内仍然适用
新知探究
两个数相乘,交换两个因数的位置,积相等.
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
1.乘法交换律:
2.乘法结合律:
数的范围已扩充到有理数.
注意:
用字母表示乘数时,“×”号可以写成“·”或省略,
如a×b可以写成a·b或ab.
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
新知探究
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
a(b+c)
ab+ac
=
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
3.乘法分配律:
巩固练习
1.计算(-3)×2×(-5)=(-3)×[2×(-5)],这是运用了( )
A.乘法交换律
B.乘法结合律
C.乘法分配律
D.乘法交换律、乘法结合律
B
巩固练习
2.用两种方法计算:
思考:可以使用哪两种方法?请你动手做一做.
巩固练习
解:
方法1:
方法2:
巩固练习
3.观察下列计算过程,看其中运用了什么运算律?运算过程是否存在错误?哪里出现了错误?请指正.
巩固练习
正解:
特别提醒:
1. 用分配律时,一定要注意符号不能弄错、弄丢;
2. 括号外一项与括号内每一项都要相乘,不能漏项.
课堂练习
1.三个数相乘积为负数,则其中负因数的个数有( )
A.1个 B.2个
C.3个 D.1个或3个
D
提示:负因数的个数为奇数,积为负数.
课堂练习
2.下面乘积中符号为正的是( )
A.
B.
C.
D.
提示:负因数的个数为偶数,积为正数.
C
课堂练习
3. 口算:
(1)(-2)×3×4×(-1)
(2)(-5)×(-3)×4×(-2)
(3)(-2)×(-2)×(-2)×(-2)
(4)(-3)×(-3)×(-3)×(-3)
=24
=-120
=16
=81
课堂练习
4.计算:
解:(1)原式=(-6)×(-4)= 24
课堂练习
4.计算:
解:(2)原式=
课堂练习
5.若a、b、c为有理数,且|a+1|+|b+2|+|c+3|=0,求(a-1)(b+2)(c-3)的值.
解:∵ |a+1|+|b+2|+|c+3|=0,
∴ a=-1,b=-2,c=-3,
则(a-1)(b+2)(c-3)=0.
课堂总结
有理数乘法运算律
1.乘法交换律:两个数相乘,交换两个因数的位置,积不变.
ab=ba
2.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变. (ab)c=a(bc)
3.乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.a(b+c)=a(b+c)
1.4.1 有理数的乘法
第2课时 有理数乘法的运算律及运用
谢谢观看
有理数
