第二章 对称图形—圆 小结与思考 (第1课时) 课件(46张PPT)
文档属性
| 名称 | 第二章 对称图形—圆 小结与思考 (第1课时) 课件(46张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 08:47:48 | ||
图片预览






文档简介
(共46张PPT)
第2章 · 对称图形—圆
小结与思考(1)
学习目标
1. 整理本章所学知识,构建本章知识框架 ;
2. 理解并掌握圆的相关概念和性质,与圆有关的位置关系.
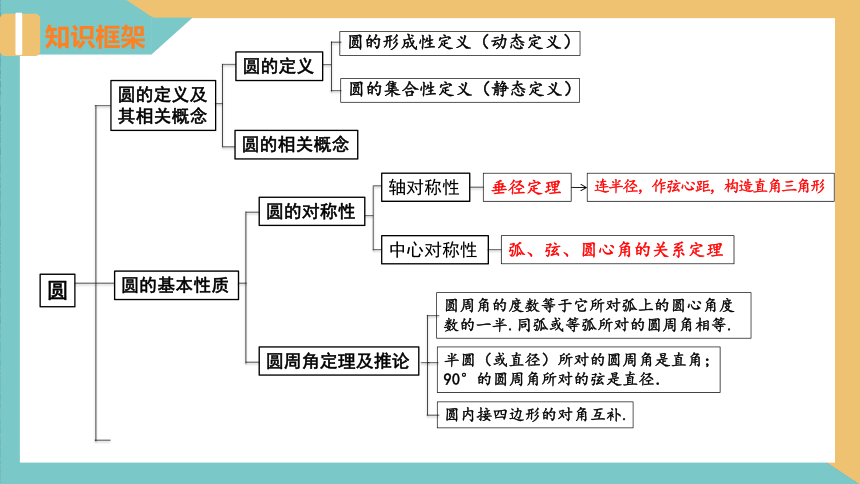
知识框架
圆
圆的定义及其相关概念
圆的形成性定义(动态定义)
圆的定义
圆的集合性定义(静态定义)
圆的相关概念
圆的基本性质
圆的对称性
轴对称性
中心对称性
垂径定理
弧、弦、圆心角的关系定理
圆周角定理及推论
圆周角的度数等于它所对弧上的圆心角度数的一半.同弧或等弧所对的圆周角相等.
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
圆内接四边形的对角互补.
连半径,作弦心距,构造直角三角形
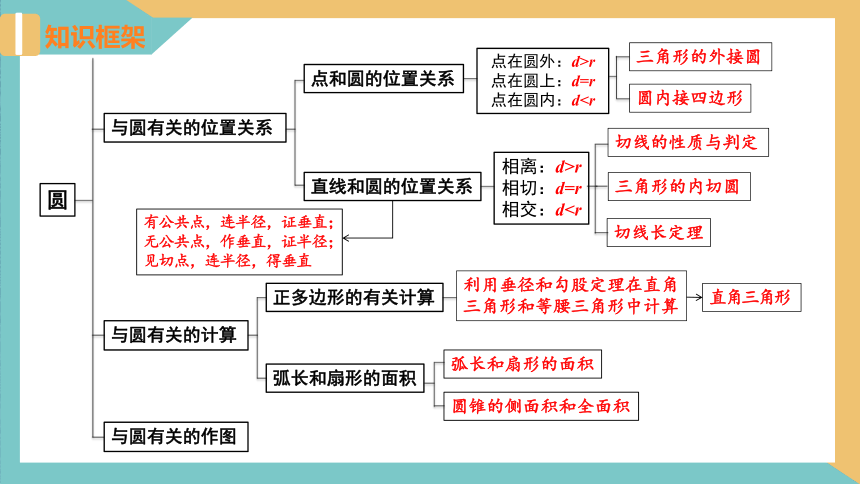
知识框架
圆
与圆有关的位置关系
点和圆的位置关系
直线和圆的位置关系
点在圆外:d>r点在圆上:d=r 点在圆内:d三角形的外接圆
圆内接四边形
相离:d>r
相切:d=r
相交:d切线的性质与判定
切线长定理
三角形的内切圆
与圆有关的计算
正多边形的有关计算
弧长和扇形的面积
利用垂径和勾股定理在直角三角形和等腰三角形中计算
弧长和扇形的面积
圆锥的侧面积和全面积
有公共点,连半径,证垂直;
无公共点,作垂直,证半径;
见切点,连半径,得垂直
直角三角形
与圆有关的作图
考点分析
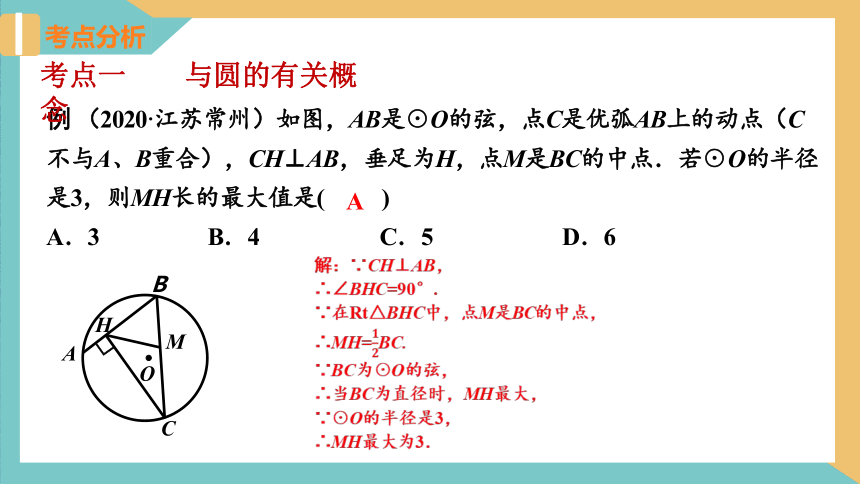
例 (2020·江苏常州)如图,AB是☉O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若☉O的半径是3,则MH长的最大值是( )
A.3 B.4 C.5 D.6
考点一 与圆的有关概念
C
B
A
O
∟
H
M
A
考点分析
1.(2021·凉山州)已知P是☉O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A. 3cm B. 4cm C. 5cm D. 6cm
B
2.(2021·江苏常州)如图,BC是☉O的直径,AB是☉O的弦.若∠AOC=60°,则∠OAB的度数是( )
A. 20° B. 25° C. 30° D. 35°
C
C
O·
B
A
巩固练习
3. 如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3:1,则圆的面积约为正方形面积的( )
A.27倍 B.14倍 C.9倍 D. 3倍
B
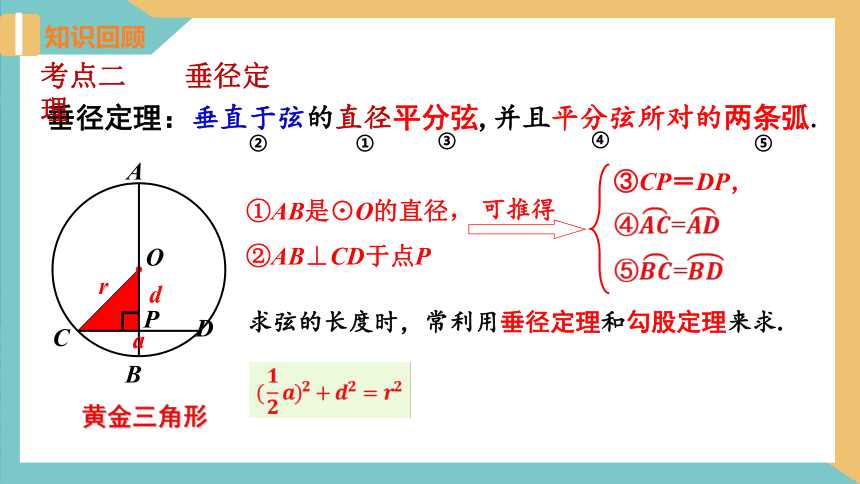
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
·
O
C
D
A
B
P
∟
①AB是⊙O的直径, ②AB⊥CD于点P
可推得
③CP=DP,
①
②
③
④
⑤
知识回顾
黄金三角形
d
a
r
求弦的长度时,常利用垂径定理和勾股定理来求.
考点二 垂径定理
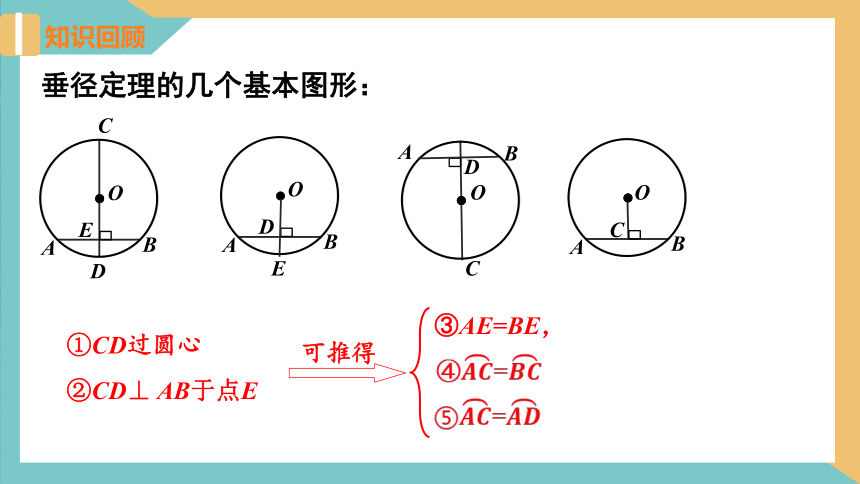
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
①CD过圆心
②CD⊥ AB于点E
可推得
③AE=BE,
知识回顾
考点分析
例 如图,四边形 ABCD是⊙O的内接四边形,且 AC⊥BD,OF⊥AB,垂足分别为 E、F. OF与CD有怎样的数量关系?为什么?
C
B
A
O
∟
E
D
∟
F
G
巩固练习
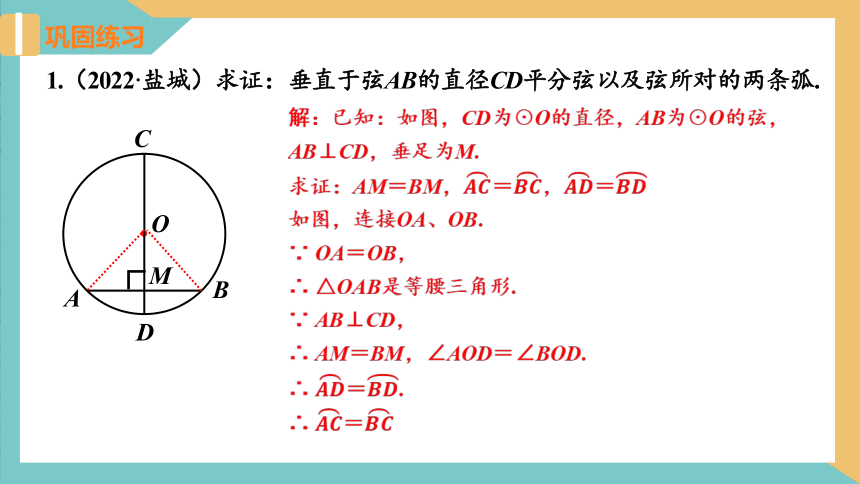
1.(2022·盐城)求证:垂直于弦AB的直径CD平分弦以及弦所对的两条弧.
·
O
A
B
C
D
M
∟
巩固练习
2.如图,BC是⊙O的弦,半径OA⊥BC,点D在⊙O上,且∠ADB =25°.求∠AOC的度数.
C
B
A
O
∟
D
巩固练习
3.如图,在⊙O中,直径AB交弦CD于点E,OF⊥CD,垂足为F,AE =1,BE=5,OF=1.求CD的长.
C
B
A
O
∟
D
F
E
1
1
5
巩固练习
4. ⊙O的半径为10cm,弦AB∥CD,AB=16,CD=12,则AB、CD间的
距离是____________.
2cm
或14cm
解:
①两条弦在圆心的同侧
②两条弦在圆心的两侧
●O
A
B
C
D
∟
●O
A
B
C
D
∟
巩固练习
5.(2020·江苏徐州)在△ABC中,若AB=6,∠ACB=45°,则△ACB的面积的最大值为_______.
A
C
B
6
45°
O
M
知识回顾
考点三 弧、弦、圆心角的关系定理
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
●
●
A
B
A'
B'
O
O'
AB=A′B′
∠AOB =∠A′O′B′
AB=A′B′
∠AOB =∠ A′O′B′
AB=A′B′
∠AOB=∠ A′O′B′
考点分析
C
B
A
O
D
E
F
G
C
B
A
O
D
E
F
G
考点分析
(2)设G是BD的中点,在⊙O上是否存在点P(点B除外),使得 PG=PF?为什么?
P
∟
巩固练习
C
B
A
O
D
E
∴∠AOC=∠COD=∠DOE.
∵∠AOC =40°,
∴∠COD=∠DOE=∠AOC =40°.
∴∠BOE=180°-3×40°=60°.
巩固练习
2.如图,AB是⊙O的直径,AC是⊙O的弦,AB= 2,∠BAC =30°.
在图中作弦AD,使 AD = 1,并求∠CAD的度数.
C
B
A
O
D1
D2
巩固练习
(1)求证:△BFG≌△CDG;
C
B
A
O
∟
D
E
F
G
巩固练习
(2) 若AD=BE=2,求BF的长.
C
B
A
O
∟
D
E
F
G
知识回顾
考点四 圆周角定理
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等.
推论1:
半圆(或直径)所对的圆周角是直角;
用于判断某个
圆周角是否是直角
用于判断某条弦是否是直径
90°的圆周角所对的弦是直径.
推论2:
圆内接四边形的对角互补.
考点分析
例 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O
的弦,且AF⊥BC,垂足为D. BE与CF相等吗?为什么?
C
B
A
O
∟
D
E
F
巩固练习
1.(2022·江苏淮安)如图,四边形ABCD是⊙O的内接四边形,若∠AOC=160°,则∠ABC的度数是 ( )
A.80° B.100° C.140° D.160°
B
2.(2020·江苏镇江)如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于 ( )
A.10° B.14° C.16° D.26°
C
B
A
O
D
O
A
B
C
D
C
图1
图2
巩固练习
3.(2021·江苏连云港)如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=30°,∠OBC=40°.则∠OAC=______.
C
B
A
O
25°
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是BC上一点,过C、E、D三点的圆交AE于点F. ∠DFE与∠BAC相等吗?为什么?
图3
C
B
A
D
F
E
∟
∟
图4
相等.
由∠ECD=∠DFE,∠ECD=∠BAC,
得∠DFE=∠BAC.
5.(1)如图①,点A、B、C在⊙O上,点D在⊙O外,比较∠BAC与∠BDC的大小,并说明理由;
(2)如图②,点A、B、C在⊙O上,点D在⊙O内,比较∠BAC与∠BDC的大小,并说明理由.
C
B
A
O
D
①
C
B
A
O
D
②
E
F
巩固练习
巩固练习
6.如图,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D. 若AB=10,AC=6,求BC、BD的长.
C
B
A
O
D
巩固练习
7.如图,四边形 ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F,且∠E=50°,∠F=30°.求∠A的度数.
C
B
A
O
D
F
E
解:∵四边形 ABCD内接于⊙O
∴∠ADC+∠ABC=180°.
∵∠E=50°,∠F=30°
∴∠ADC+∠A=150°,
∠ABC+∠A=130°.
∴∠ADC+∠ABC+2∠A=280°.
180°+2∠A=280°.
∴∠A=50°
考点五 点与圆的位置关系
知识回顾
d
d
点在圆内
点在圆上
点在圆外
O
P
P
P
●
O
P
●
O
P
●
O
P
r
r
r
d
d<r
d=r
d>r
点与圆的位置关系
d与r的数量关系
考点分析
例 如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为坐标轴、网格边长为单位长,建立平面直角坐标系;②利用网格,仅用直尺画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
A
B
C
O
D
x
y
(2)请在(1)的基础上,完成下列问题:
①点C的坐标是 ;
点D的坐标是 ;
②⊙D的半径= (结果保留根号).
(6,2)
(2,0)
巩固练习
1. 在△ABC中, ∠C=90 °,AC=1,BC=2,M是AB的中点,以点C为圆心,1为半径作⊙C,则( )
A. 点M在⊙C上 B.点M在⊙C内
C.点M在⊙C外 D.点M与⊙C的位置关系不能确定
C
2.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为___________.
2cm或4cm
3.在公园的点O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一个以点O为圆心、OA长为半径的圆形水池,要求池内不留树,则E、F、G、H四棵树中需要被移除的为( )
A
巩固练习
A. E、F、G B. F、G、H C. G、H、E D. H、E、F
H
A
O
G
F
E
直线与圆的
位置关系 相 交 相 切 相 离
图形
公共点个数
公共点名称
直线名称
圆心到直线的距离
d与半径r的关系
知识回顾
● O
2
d
r
d<r
● O
d
r
1
d=r
● O
d
r
d>r
切点
切线
0
考点六 直线与圆的位置关系
三角形内切圆和外接中的有关角
基本图形
角之间的关系
∠BOC=2∠A
知识回顾
a
b
c
1.有哪些方法可以判定直线与圆相切?
1.定义法:
2.数量关系法(d=r)
3.判定定理
l
A
l
O
l
r
d
知识回顾
2.常用辅助线添加方法:
证切线时常用辅助线添加方法:
①有交点,连半径,证垂直;
②无交点,作垂直,证相等(d=r).
有切线时常用辅助线添加方法:
有切点,连半径,得垂直
考点分析
例1 在同一平面内,已知点O到直线l的距离为5,以点O为圆心,r为半径画圆.
(1)当r=_____时,⊙O上有且只有1个点到直线l的距离等于3;
(2)当r=_____时,⊙O上有且只有3个点到直线l的距离等于3;
(3)随着r的变化,⊙O上到直线l的距离等于3的点的个数有哪些变化?求出相对应的r的值或取值范围.
O
l
∟
(1)5-3=2
5
2
3
3
(2)5+3=8
8
(3)当0当r=2时, ⊙O上有且只有1个点到直线l的距离等于3;
当2当r=8时, ⊙O上有且只有3个点到直线l的距离等于3,
当r>8时, ⊙O上有且只有4个点到直线l的距离等于3.
分类讨论思想
巩固练习
1.(2023·江苏宿迁)在同一平面内,已知⊙O的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P到直线l的最大距离是______.
5
l
O
P
∟
2.(2020·江苏泰州)如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为_______.
图1
∟
a
b
O
P
H
3或5
图2
3.如图,直线AB、CD相交于点O, ∠AOD=30 °,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么__________秒钟后⊙P与直线CD相切.
4或8
o
A
B
D
C
P
P1
P2
E
巩固练习
例2 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
M
N
D
O
A
B
C
证明:过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,
∴OM⊥BC.
又∵ON⊥CD,O为正方形ABCD
对角线AC上一点,
∴OM=ON,
∴CD与⊙O相切.
┛
切线的判定和性质综合应用.
无交点,作垂直,证相等(d=r)
考点分析
巩固练习
1.如图,AD是⊙O的弦,AB经过圆心O交⊙O于点C,∠A=∠B=30°.
BD与⊙O有怎样的位置关系?为什么?
C
B
A
O
D
解:连接OD.
∵OA=OD,
∴∠ADO=∠A=30°,
∴∠BOD=60°.
又∵∠B=30°,
∴∠BDO=90°.
∴直线BD与⊙O相切.
巩固练习
2.如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,∠BAC=2∠B,过点A的切线交OC的延长线于点D.若⊙O的半径为2,求AD的长.
C
B
A
O
D
巩固练习
3. 如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,且∠BAD=80°. 求∠DAC的度数.
C
A
B
O
D
∟
巩固练习
4. 如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别为A、B.
OP与CB有怎样的位置关系?为什么?
C
B
A
O
P
解:连接AB、OB.
∵PA、PB是⊙O的切线,
∴PA=PB,
∵OA=OB,
∴OP⊥AB.
∵AC是⊙O的直径,
∴∠ABC=90°.
∴CB⊥AB.
∴OP∥CB.
巩固练习
5.如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分
别为D、E、F.若BD=6,AD=4,求⊙O的半径r.
∟
C
B
A
O
F
D
E
解:连接OE、OF.设⊙O的半径为r.
∵BC、AC是⊙O的切线,
∴CE=CF,OE⊥BC,OF⊥AC,
∵∠C=90°,
∴四边形OECF是正方形.
在Rt△ABC中,
∵AB=10,BC=6+r,CA=4+r,
得(6+r)2+(4+r)2=102,
∴r=2.
课堂小结
谈谈你本节课的收获是什么?
第2章 · 对称图形—圆
小结与思考(1)
学习目标
1. 整理本章所学知识,构建本章知识框架 ;
2. 理解并掌握圆的相关概念和性质,与圆有关的位置关系.
知识框架
圆
圆的定义及其相关概念
圆的形成性定义(动态定义)
圆的定义
圆的集合性定义(静态定义)
圆的相关概念
圆的基本性质
圆的对称性
轴对称性
中心对称性
垂径定理
弧、弦、圆心角的关系定理
圆周角定理及推论
圆周角的度数等于它所对弧上的圆心角度数的一半.同弧或等弧所对的圆周角相等.
半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
圆内接四边形的对角互补.
连半径,作弦心距,构造直角三角形
知识框架
圆
与圆有关的位置关系
点和圆的位置关系
直线和圆的位置关系
点在圆外:d>r点在圆上:d=r 点在圆内:d
圆内接四边形
相离:d>r
相切:d=r
相交:d
切线长定理
三角形的内切圆
与圆有关的计算
正多边形的有关计算
弧长和扇形的面积
利用垂径和勾股定理在直角三角形和等腰三角形中计算
弧长和扇形的面积
圆锥的侧面积和全面积
有公共点,连半径,证垂直;
无公共点,作垂直,证半径;
见切点,连半径,得垂直
直角三角形
与圆有关的作图
考点分析
例 (2020·江苏常州)如图,AB是☉O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若☉O的半径是3,则MH长的最大值是( )
A.3 B.4 C.5 D.6
考点一 与圆的有关概念
C
B
A
O
∟
H
M
A
考点分析
1.(2021·凉山州)已知P是☉O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A. 3cm B. 4cm C. 5cm D. 6cm
B
2.(2021·江苏常州)如图,BC是☉O的直径,AB是☉O的弦.若∠AOC=60°,则∠OAB的度数是( )
A. 20° B. 25° C. 30° D. 35°
C
C
O·
B
A
巩固练习
3. 如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3:1,则圆的面积约为正方形面积的( )
A.27倍 B.14倍 C.9倍 D. 3倍
B
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
·
O
C
D
A
B
P
∟
①AB是⊙O的直径, ②AB⊥CD于点P
可推得
③CP=DP,
①
②
③
④
⑤
知识回顾
黄金三角形
d
a
r
求弦的长度时,常利用垂径定理和勾股定理来求.
考点二 垂径定理
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
①CD过圆心
②CD⊥ AB于点E
可推得
③AE=BE,
知识回顾
考点分析
例 如图,四边形 ABCD是⊙O的内接四边形,且 AC⊥BD,OF⊥AB,垂足分别为 E、F. OF与CD有怎样的数量关系?为什么?
C
B
A
O
∟
E
D
∟
F
G
巩固练习
1.(2022·盐城)求证:垂直于弦AB的直径CD平分弦以及弦所对的两条弧.
·
O
A
B
C
D
M
∟
巩固练习
2.如图,BC是⊙O的弦,半径OA⊥BC,点D在⊙O上,且∠ADB =25°.求∠AOC的度数.
C
B
A
O
∟
D
巩固练习
3.如图,在⊙O中,直径AB交弦CD于点E,OF⊥CD,垂足为F,AE =1,BE=5,OF=1.求CD的长.
C
B
A
O
∟
D
F
E
1
1
5
巩固练习
4. ⊙O的半径为10cm,弦AB∥CD,AB=16,CD=12,则AB、CD间的
距离是____________.
2cm
或14cm
解:
①两条弦在圆心的同侧
②两条弦在圆心的两侧
●O
A
B
C
D
∟
●O
A
B
C
D
∟
巩固练习
5.(2020·江苏徐州)在△ABC中,若AB=6,∠ACB=45°,则△ACB的面积的最大值为_______.
A
C
B
6
45°
O
M
知识回顾
考点三 弧、弦、圆心角的关系定理
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
●
●
A
B
A'
B'
O
O'
AB=A′B′
∠AOB =∠A′O′B′
AB=A′B′
∠AOB =∠ A′O′B′
AB=A′B′
∠AOB=∠ A′O′B′
考点分析
C
B
A
O
D
E
F
G
C
B
A
O
D
E
F
G
考点分析
(2)设G是BD的中点,在⊙O上是否存在点P(点B除外),使得 PG=PF?为什么?
P
∟
巩固练习
C
B
A
O
D
E
∴∠AOC=∠COD=∠DOE.
∵∠AOC =40°,
∴∠COD=∠DOE=∠AOC =40°.
∴∠BOE=180°-3×40°=60°.
巩固练习
2.如图,AB是⊙O的直径,AC是⊙O的弦,AB= 2,∠BAC =30°.
在图中作弦AD,使 AD = 1,并求∠CAD的度数.
C
B
A
O
D1
D2
巩固练习
(1)求证:△BFG≌△CDG;
C
B
A
O
∟
D
E
F
G
巩固练习
(2) 若AD=BE=2,求BF的长.
C
B
A
O
∟
D
E
F
G
知识回顾
考点四 圆周角定理
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等.
推论1:
半圆(或直径)所对的圆周角是直角;
用于判断某个
圆周角是否是直角
用于判断某条弦是否是直径
90°的圆周角所对的弦是直径.
推论2:
圆内接四边形的对角互补.
考点分析
例 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O
的弦,且AF⊥BC,垂足为D. BE与CF相等吗?为什么?
C
B
A
O
∟
D
E
F
巩固练习
1.(2022·江苏淮安)如图,四边形ABCD是⊙O的内接四边形,若∠AOC=160°,则∠ABC的度数是 ( )
A.80° B.100° C.140° D.160°
B
2.(2020·江苏镇江)如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于 ( )
A.10° B.14° C.16° D.26°
C
B
A
O
D
O
A
B
C
D
C
图1
图2
巩固练习
3.(2021·江苏连云港)如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=30°,∠OBC=40°.则∠OAC=______.
C
B
A
O
25°
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是BC上一点,过C、E、D三点的圆交AE于点F. ∠DFE与∠BAC相等吗?为什么?
图3
C
B
A
D
F
E
∟
∟
图4
相等.
由∠ECD=∠DFE,∠ECD=∠BAC,
得∠DFE=∠BAC.
5.(1)如图①,点A、B、C在⊙O上,点D在⊙O外,比较∠BAC与∠BDC的大小,并说明理由;
(2)如图②,点A、B、C在⊙O上,点D在⊙O内,比较∠BAC与∠BDC的大小,并说明理由.
C
B
A
O
D
①
C
B
A
O
D
②
E
F
巩固练习
巩固练习
6.如图,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D. 若AB=10,AC=6,求BC、BD的长.
C
B
A
O
D
巩固练习
7.如图,四边形 ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F,且∠E=50°,∠F=30°.求∠A的度数.
C
B
A
O
D
F
E
解:∵四边形 ABCD内接于⊙O
∴∠ADC+∠ABC=180°.
∵∠E=50°,∠F=30°
∴∠ADC+∠A=150°,
∠ABC+∠A=130°.
∴∠ADC+∠ABC+2∠A=280°.
180°+2∠A=280°.
∴∠A=50°
考点五 点与圆的位置关系
知识回顾
d
d
点在圆内
点在圆上
点在圆外
O
P
P
P
●
O
P
●
O
P
●
O
P
r
r
r
d
d<r
d=r
d>r
点与圆的位置关系
d与r的数量关系
考点分析
例 如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为坐标轴、网格边长为单位长,建立平面直角坐标系;②利用网格,仅用直尺画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
A
B
C
O
D
x
y
(2)请在(1)的基础上,完成下列问题:
①点C的坐标是 ;
点D的坐标是 ;
②⊙D的半径= (结果保留根号).
(6,2)
(2,0)
巩固练习
1. 在△ABC中, ∠C=90 °,AC=1,BC=2,M是AB的中点,以点C为圆心,1为半径作⊙C,则( )
A. 点M在⊙C上 B.点M在⊙C内
C.点M在⊙C外 D.点M与⊙C的位置关系不能确定
C
2.平面上一点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为___________.
2cm或4cm
3.在公园的点O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一个以点O为圆心、OA长为半径的圆形水池,要求池内不留树,则E、F、G、H四棵树中需要被移除的为( )
A
巩固练习
A. E、F、G B. F、G、H C. G、H、E D. H、E、F
H
A
O
G
F
E
直线与圆的
位置关系 相 交 相 切 相 离
图形
公共点个数
公共点名称
直线名称
圆心到直线的距离
d与半径r的关系
知识回顾
● O
2
d
r
d<r
● O
d
r
1
d=r
● O
d
r
d>r
切点
切线
0
考点六 直线与圆的位置关系
三角形内切圆和外接中的有关角
基本图形
角之间的关系
∠BOC=2∠A
知识回顾
a
b
c
1.有哪些方法可以判定直线与圆相切?
1.定义法:
2.数量关系法(d=r)
3.判定定理
l
A
l
O
l
r
d
知识回顾
2.常用辅助线添加方法:
证切线时常用辅助线添加方法:
①有交点,连半径,证垂直;
②无交点,作垂直,证相等(d=r).
有切线时常用辅助线添加方法:
有切点,连半径,得垂直
考点分析
例1 在同一平面内,已知点O到直线l的距离为5,以点O为圆心,r为半径画圆.
(1)当r=_____时,⊙O上有且只有1个点到直线l的距离等于3;
(2)当r=_____时,⊙O上有且只有3个点到直线l的距离等于3;
(3)随着r的变化,⊙O上到直线l的距离等于3的点的个数有哪些变化?求出相对应的r的值或取值范围.
O
l
∟
(1)5-3=2
5
2
3
3
(2)5+3=8
8
(3)当0
当2
当r>8时, ⊙O上有且只有4个点到直线l的距离等于3.
分类讨论思想
巩固练习
1.(2023·江苏宿迁)在同一平面内,已知⊙O的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P到直线l的最大距离是______.
5
l
O
P
∟
2.(2020·江苏泰州)如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为_______.
图1
∟
a
b
O
P
H
3或5
图2
3.如图,直线AB、CD相交于点O, ∠AOD=30 °,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么__________秒钟后⊙P与直线CD相切.
4或8
o
A
B
D
C
P
P1
P2
E
巩固练习
例2 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
M
N
D
O
A
B
C
证明:过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,
∴OM⊥BC.
又∵ON⊥CD,O为正方形ABCD
对角线AC上一点,
∴OM=ON,
∴CD与⊙O相切.
┛
切线的判定和性质综合应用.
无交点,作垂直,证相等(d=r)
考点分析
巩固练习
1.如图,AD是⊙O的弦,AB经过圆心O交⊙O于点C,∠A=∠B=30°.
BD与⊙O有怎样的位置关系?为什么?
C
B
A
O
D
解:连接OD.
∵OA=OD,
∴∠ADO=∠A=30°,
∴∠BOD=60°.
又∵∠B=30°,
∴∠BDO=90°.
∴直线BD与⊙O相切.
巩固练习
2.如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,∠BAC=2∠B,过点A的切线交OC的延长线于点D.若⊙O的半径为2,求AD的长.
C
B
A
O
D
巩固练习
3. 如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,且∠BAD=80°. 求∠DAC的度数.
C
A
B
O
D
∟
巩固练习
4. 如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别为A、B.
OP与CB有怎样的位置关系?为什么?
C
B
A
O
P
解:连接AB、OB.
∵PA、PB是⊙O的切线,
∴PA=PB,
∵OA=OB,
∴OP⊥AB.
∵AC是⊙O的直径,
∴∠ABC=90°.
∴CB⊥AB.
∴OP∥CB.
巩固练习
5.如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分
别为D、E、F.若BD=6,AD=4,求⊙O的半径r.
∟
C
B
A
O
F
D
E
解:连接OE、OF.设⊙O的半径为r.
∵BC、AC是⊙O的切线,
∴CE=CF,OE⊥BC,OF⊥AC,
∵∠C=90°,
∴四边形OECF是正方形.
在Rt△ABC中,
∵AB=10,BC=6+r,CA=4+r,
得(6+r)2+(4+r)2=102,
∴r=2.
课堂小结
谈谈你本节课的收获是什么?
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
