1.4.1 有理数的乘法(第1课时) 课件(29张PPT)
文档属性
| 名称 | 1.4.1 有理数的乘法(第1课时) 课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 593.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 09:34:58 | ||
图片预览







文档简介
(共29张PPT)
新课导入
讲授新课
当堂检测
课堂小结
第一章 有理数
1.4 有理数的乘除法
1.4.1 有理数的乘法(第1课时)
情景引入
情景引入
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库的水位高低?
思考:有没有发现这一问题有什么漏洞?
若问句改成:4天后甲、乙水库的水位的总变化量各是多少?
知识点一 有理数的乘法法则
知识精讲
0
500
1000
1500
-500
-1000
-1500
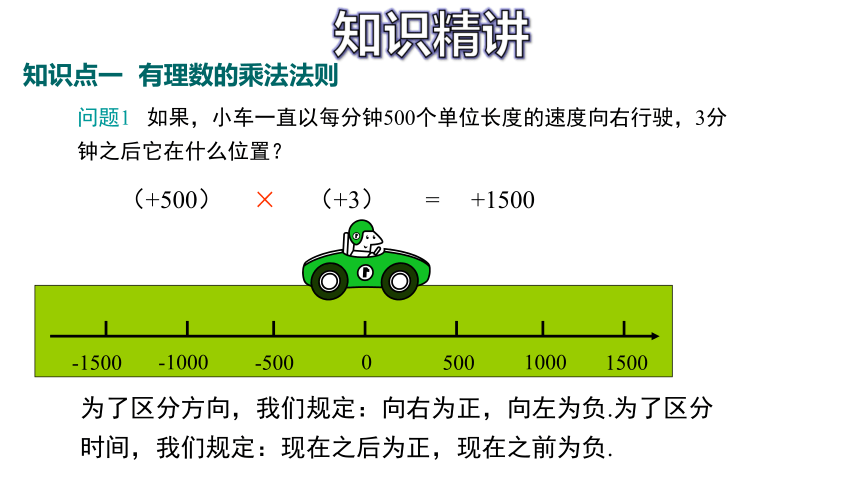
问题1 如果,小车一直以每分钟500个单位长度的速度向右行驶,3分钟之后它在什么位置?
(+500)
×
(+3)
= +1500
为了区分方向,我们规定:向右为正,向左为负.为了区分时间,我们规定:现在之后为正,现在之前为负.
知识精讲
0
500
1000
1500
-500
-1000
-1500
问题2 如果,小车一直以每分钟500个单位长度的速度向左行驶,3分钟之后它在什么位置?
(-500)
×
(+3)
= -1500
知识精讲
0
500
1000
1500
-500
-1000
-1500
问题3 如果,小车一直以每分钟500个单位长度的速度向右行驶,3分钟之前它在什么位置?
(+500)
×
(-3)
= -1500
知识精讲
0
500
1000
1500
-500
-1000
-1500
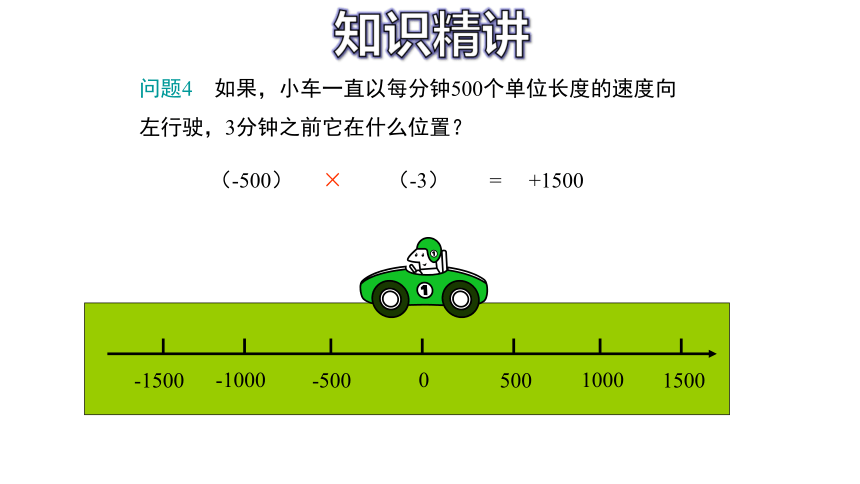
问题4 如果,小车一直以每分钟500个单位长度的速度向左行驶,3分钟之前它在什么位置?
(-500)
×
(-3)
= +1500
知识精讲
通过上例,我们得到4个式子:
(+500)×(+3) = +1500
(- 500)×(-3) = + 1500
(+500)×(- 3) = -1500
(- 500)×(+ 3) = -1500
想一想:
积的符号与两因数的符号有什么关系?
积的绝对值与两因数的绝对值有什么关系?
知识精讲
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
讨论:
(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
概念总结
知识精讲
几个不等于零的数相乘,积的符号由__________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
知识归纳:
几个数相乘,如果其中有因数为0,_________
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
典型例题
典例精析
【例1】下列计算中,得数最小的是( )
A.-3×() B.3×() C.-3×() D.3×()
【详解】解:A、-3×( )=1;
B、3×( )=2;
C、-3×( )=-1;
D、3×( )=-2;
∵2>1>-1>-2,
∴得数最小的是D选项,
故选:D.
练一练
1.从数-8,0,-3,4,1中任取两个数相乘,其最小的积是 .
【详解】在数-8,0,-3,4,1中任取两个数相乘,最小的积是-8×4=-32;
故答案为:-32.
2.计算:
(1); (2).
【详解】(1)原式=;
(2)原式=;
知识点二 倒数
知识精讲
计算并观察结果有何特点?
(1) ×2; (2)(-0.25)×(-4)
要点:有理数中,乘积是1的两个数互为倒数.
思考:数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
知识补充:何为负倒数——乘积为-1的两个数
典型例题
典例精析
【例2】一个数的倒数是它本身,那么这个数是( )
A.0 B.0或1 C.1或-1 D.0或±1
【详解】解:∵1×1=1,
∴1的倒数是1,
∵-1×(-1)=1,
∴-1的倒数是-1,
∵0没有倒数,
∴这个数是1或-1.
故选:C.
练一练
1.做一做:
①5的倒数是 ; ②2的倒数是 ;
③0.1的倒数是 ; ④-3.75的倒数是 ;
⑤-3的倒数是 ; ⑥-0.15的倒数是 .
【答案】 10
【点睛】本题考查了倒数的定义,解决本题的关键是掌握倒数的定义:分子和分母相倒并且两个乘积是1的数互为倒数,0没有倒数.
2.已知x的倒数是,y的绝对值是8,x+y>0,求x-y的值.
【详解】解:因为x的倒数是,
所以x=-2.
因为y的绝对值是8,x+y>0,
所以y=8,
所以x-y=-2-8=-10.
典例精析
【例3】某厂规定,工人完成定额20个零件,每天收入28元,如果超额生产一个零件,增加收入1.5元.一工人某天生产了26个零件,则该工人此天收入( )
A.39元 B.38元 C.37元 D.36元
【详解】解:定额20个零件,收入28元,某天生产了26个零件,
∴超额26-20=6(个),
∵超额生产一个零件,增加收入1.5元,
∴超额6个的费用是1.5×6=9(元),
∴该工人此天收入28+9=37(元),
故选:C.
知识点三 有理数乘法的应用
知识精讲
练一练
1.人的正常体温一般在37℃左右,室温太高、太低都会感到不舒服.研究认为,人的满意温度与人的正常体温的比是0.618,则该温度约为 ℃.(结果精确到0.1)
【详解】解:∵人的满意温度与人的正常体温的比是0.618,正常人的体温一般在37℃,
∴人的满意温度37=0.618,
∴人的满意温度约为37×0.618≈22.9℃.
故答案为:22.9.
2.高速公路养护小组,乘车沿东西方向的公路巡视维护,约定向东为正,向西为负,当天行驶记录如下(单位:千米):+18,-9,+17,-14,-3,+11,-6,-8.
(1)养护小组最后到达的地方在出发点的哪个方向?距出发点多远?
(2)养护过程中,最远处离出发点有多远?
(3)若汽车行驶每千米耗油量为0.1升,则这次养护小组的汽车共耗油多少升?
【详解】(1)解:+18+(-9)+(+17)+(-14)+(-3)+(+11)+(-6)+
(-8)=6(千米),
故最后到达的地方在出发点东方,距出发点6千米;
(2)解:距离出发点的距离依次为:18、9、26、12、9、20、14、6.
所以,最远处离出发点26千米;
(3)解:18+9+17+14+3+11+6+8=86(千米),
86×0.1=8.6升.
答:这次养护小组的汽车共耗油8.6升.
课堂练习
1.计算(-5)×(-25)×(-2)×4的结果是( )
A.-100 B.100 C.-1000 D.1000
【详解】解:原式=[(-5)×(-2)]×[(-25)×4]
=10×(100)
=-1000,
故选:C.
2.小明的爸爸月工资为6000元,扣除5000元个税免征额后,爸爸剩余的部分需要按3%的税率缴纳个人所得税,小明的爸爸应缴纳个人所得税( )元.
A.135 B.105 C.30 D.165
【详解】解:(6000-5000)×3%
=1000×3%
=30(元)
故选:C.
3.如果a,b,c为非零有理数且abc<0,那么的所有可能的值为( )
A.0 B.1或-1 C.1或-3 D.-2或3
【详解】解:abc<0,
∴a,b,c有1个或者3个负数,
∴当a,b,c有1个负数时,=1+1-1=1,
当a,b,c有3个负数时,=-1-1-1=-3,
故选C.
4.在数4、-6、3、-2、1中,任意取3个不同的数相乘,其中乘积最大是 .
【详解】解:乘积最大一定为正数,当三个因数都为正数时,积为1×3×4=12,当由两个因数为负数,另一个为最大的正数时,积为
-6×(-2)×4=48,
∵48>12,
∴乘积最大是48;
故答案为:48
5.已知m、n互为相反数,c、d互为倒数,则m+n+3cd-10的值为 .
【详解】解:∵m、n互为相反数,c、d互为倒数,
∴m+n=0,cd=1,
∴m+n+3cd-10=0+3×1-10=-7,
故答案为:-7.
6.低碳生活就是让我们从身边的小事做起,珍惜资源,降低能耗.已知家用自来水二氧化碳的排放量(kg)=自来水使用吨数(t)×0.91,若聪聪家某个月的用水量为6t,则这个月聪聪家自来水二氧化碳的排放量为 kg.
【详解】解:由题意,得这个月聪聪家自来水二氧化碳的排放量为6×0.91=5.46kg;
故答案为:5.46
7.计算:
(1)(-10)×()×(-0,1)×6; (2)-3×××(-0.25).
【详解】(1)解:原式==-2.
(2)解:原式=3×××=.
8.某大学游泳池暑假开展优惠活动,普通票价每张20元,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费;②银卡售价150元/张,每次凭卡另收10元.两种优惠卡仅限暑假使用,不限次数,大学生张佳打算在40天的假期内每天游泳一次,选择哪种消费方式更合算?
【详解】解:方式一:普通票总消费金额为:20×40=800(元);
方式二:金卡总消费金额为600元;
方式三:银卡总消费金额为:150+10×40=550(元).
∵550<600<800,
∴选择银卡消费方式消费更合算.
课堂总结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.任何数和零相乘都得零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
新课导入
讲授新课
当堂检测
课堂小结
第一章 有理数
1.4 有理数的乘除法
1.4.1 有理数的乘法(第1课时)
情景引入
情景引入
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库的水位高低?
思考:有没有发现这一问题有什么漏洞?
若问句改成:4天后甲、乙水库的水位的总变化量各是多少?
知识点一 有理数的乘法法则
知识精讲
0
500
1000
1500
-500
-1000
-1500
问题1 如果,小车一直以每分钟500个单位长度的速度向右行驶,3分钟之后它在什么位置?
(+500)
×
(+3)
= +1500
为了区分方向,我们规定:向右为正,向左为负.为了区分时间,我们规定:现在之后为正,现在之前为负.
知识精讲
0
500
1000
1500
-500
-1000
-1500
问题2 如果,小车一直以每分钟500个单位长度的速度向左行驶,3分钟之后它在什么位置?
(-500)
×
(+3)
= -1500
知识精讲
0
500
1000
1500
-500
-1000
-1500
问题3 如果,小车一直以每分钟500个单位长度的速度向右行驶,3分钟之前它在什么位置?
(+500)
×
(-3)
= -1500
知识精讲
0
500
1000
1500
-500
-1000
-1500
问题4 如果,小车一直以每分钟500个单位长度的速度向左行驶,3分钟之前它在什么位置?
(-500)
×
(-3)
= +1500
知识精讲
通过上例,我们得到4个式子:
(+500)×(+3) = +1500
(- 500)×(-3) = + 1500
(+500)×(- 3) = -1500
(- 500)×(+ 3) = -1500
想一想:
积的符号与两因数的符号有什么关系?
积的绝对值与两因数的绝对值有什么关系?
知识精讲
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数同0相乘,都得0.
讨论:
(1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
概念总结
知识精讲
几个不等于零的数相乘,积的符号由__________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
知识归纳:
几个数相乘,如果其中有因数为0,_________
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
典型例题
典例精析
【例1】下列计算中,得数最小的是( )
A.-3×() B.3×() C.-3×() D.3×()
【详解】解:A、-3×( )=1;
B、3×( )=2;
C、-3×( )=-1;
D、3×( )=-2;
∵2>1>-1>-2,
∴得数最小的是D选项,
故选:D.
练一练
1.从数-8,0,-3,4,1中任取两个数相乘,其最小的积是 .
【详解】在数-8,0,-3,4,1中任取两个数相乘,最小的积是-8×4=-32;
故答案为:-32.
2.计算:
(1); (2).
【详解】(1)原式=;
(2)原式=;
知识点二 倒数
知识精讲
计算并观察结果有何特点?
(1) ×2; (2)(-0.25)×(-4)
要点:有理数中,乘积是1的两个数互为倒数.
思考:数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
知识补充:何为负倒数——乘积为-1的两个数
典型例题
典例精析
【例2】一个数的倒数是它本身,那么这个数是( )
A.0 B.0或1 C.1或-1 D.0或±1
【详解】解:∵1×1=1,
∴1的倒数是1,
∵-1×(-1)=1,
∴-1的倒数是-1,
∵0没有倒数,
∴这个数是1或-1.
故选:C.
练一练
1.做一做:
①5的倒数是 ; ②2的倒数是 ;
③0.1的倒数是 ; ④-3.75的倒数是 ;
⑤-3的倒数是 ; ⑥-0.15的倒数是 .
【答案】 10
【点睛】本题考查了倒数的定义,解决本题的关键是掌握倒数的定义:分子和分母相倒并且两个乘积是1的数互为倒数,0没有倒数.
2.已知x的倒数是,y的绝对值是8,x+y>0,求x-y的值.
【详解】解:因为x的倒数是,
所以x=-2.
因为y的绝对值是8,x+y>0,
所以y=8,
所以x-y=-2-8=-10.
典例精析
【例3】某厂规定,工人完成定额20个零件,每天收入28元,如果超额生产一个零件,增加收入1.5元.一工人某天生产了26个零件,则该工人此天收入( )
A.39元 B.38元 C.37元 D.36元
【详解】解:定额20个零件,收入28元,某天生产了26个零件,
∴超额26-20=6(个),
∵超额生产一个零件,增加收入1.5元,
∴超额6个的费用是1.5×6=9(元),
∴该工人此天收入28+9=37(元),
故选:C.
知识点三 有理数乘法的应用
知识精讲
练一练
1.人的正常体温一般在37℃左右,室温太高、太低都会感到不舒服.研究认为,人的满意温度与人的正常体温的比是0.618,则该温度约为 ℃.(结果精确到0.1)
【详解】解:∵人的满意温度与人的正常体温的比是0.618,正常人的体温一般在37℃,
∴人的满意温度37=0.618,
∴人的满意温度约为37×0.618≈22.9℃.
故答案为:22.9.
2.高速公路养护小组,乘车沿东西方向的公路巡视维护,约定向东为正,向西为负,当天行驶记录如下(单位:千米):+18,-9,+17,-14,-3,+11,-6,-8.
(1)养护小组最后到达的地方在出发点的哪个方向?距出发点多远?
(2)养护过程中,最远处离出发点有多远?
(3)若汽车行驶每千米耗油量为0.1升,则这次养护小组的汽车共耗油多少升?
【详解】(1)解:+18+(-9)+(+17)+(-14)+(-3)+(+11)+(-6)+
(-8)=6(千米),
故最后到达的地方在出发点东方,距出发点6千米;
(2)解:距离出发点的距离依次为:18、9、26、12、9、20、14、6.
所以,最远处离出发点26千米;
(3)解:18+9+17+14+3+11+6+8=86(千米),
86×0.1=8.6升.
答:这次养护小组的汽车共耗油8.6升.
课堂练习
1.计算(-5)×(-25)×(-2)×4的结果是( )
A.-100 B.100 C.-1000 D.1000
【详解】解:原式=[(-5)×(-2)]×[(-25)×4]
=10×(100)
=-1000,
故选:C.
2.小明的爸爸月工资为6000元,扣除5000元个税免征额后,爸爸剩余的部分需要按3%的税率缴纳个人所得税,小明的爸爸应缴纳个人所得税( )元.
A.135 B.105 C.30 D.165
【详解】解:(6000-5000)×3%
=1000×3%
=30(元)
故选:C.
3.如果a,b,c为非零有理数且abc<0,那么的所有可能的值为( )
A.0 B.1或-1 C.1或-3 D.-2或3
【详解】解:abc<0,
∴a,b,c有1个或者3个负数,
∴当a,b,c有1个负数时,=1+1-1=1,
当a,b,c有3个负数时,=-1-1-1=-3,
故选C.
4.在数4、-6、3、-2、1中,任意取3个不同的数相乘,其中乘积最大是 .
【详解】解:乘积最大一定为正数,当三个因数都为正数时,积为1×3×4=12,当由两个因数为负数,另一个为最大的正数时,积为
-6×(-2)×4=48,
∵48>12,
∴乘积最大是48;
故答案为:48
5.已知m、n互为相反数,c、d互为倒数,则m+n+3cd-10的值为 .
【详解】解:∵m、n互为相反数,c、d互为倒数,
∴m+n=0,cd=1,
∴m+n+3cd-10=0+3×1-10=-7,
故答案为:-7.
6.低碳生活就是让我们从身边的小事做起,珍惜资源,降低能耗.已知家用自来水二氧化碳的排放量(kg)=自来水使用吨数(t)×0.91,若聪聪家某个月的用水量为6t,则这个月聪聪家自来水二氧化碳的排放量为 kg.
【详解】解:由题意,得这个月聪聪家自来水二氧化碳的排放量为6×0.91=5.46kg;
故答案为:5.46
7.计算:
(1)(-10)×()×(-0,1)×6; (2)-3×××(-0.25).
【详解】(1)解:原式==-2.
(2)解:原式=3×××=.
8.某大学游泳池暑假开展优惠活动,普通票价每张20元,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费;②银卡售价150元/张,每次凭卡另收10元.两种优惠卡仅限暑假使用,不限次数,大学生张佳打算在40天的假期内每天游泳一次,选择哪种消费方式更合算?
【详解】解:方式一:普通票总消费金额为:20×40=800(元);
方式二:金卡总消费金额为600元;
方式三:银卡总消费金额为:150+10×40=550(元).
∵550<600<800,
∴选择银卡消费方式消费更合算.
课堂总结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.任何数和零相乘都得零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
