第二十一章 一元二次方程 单元复习课件(44张PPT)
文档属性
| 名称 | 第二十一章 一元二次方程 单元复习课件(44张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 09:54:56 | ||
图片预览





文档简介
(共44张PPT)
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十一章一元二次方程小结
学习目标
1)了解一元二次方程及其相关概念,会用配方法、公式法、分解因式法解一元二次方程,并在解一元二次方程的过程中体会转换、降次等数学思想。
2)通过根的判别式判断一元二次方程的情况,了解根与系数的关系。
3)能够利用一元二次方程解决有关实际问题,能根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力。
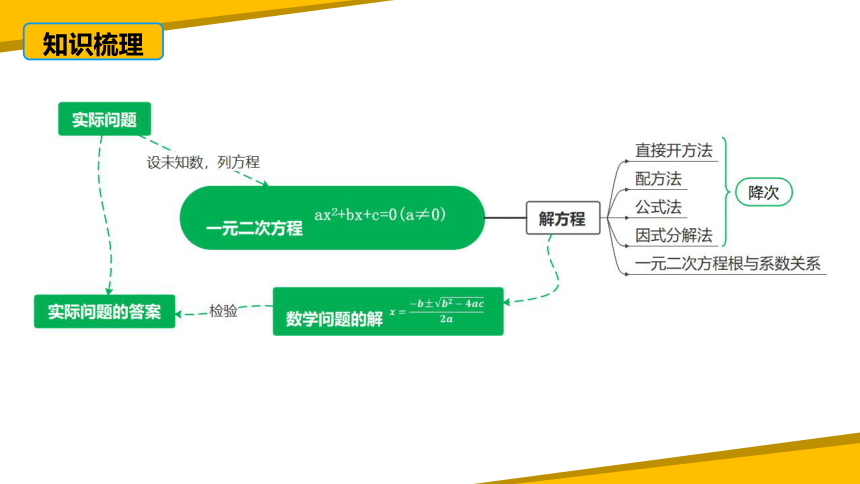
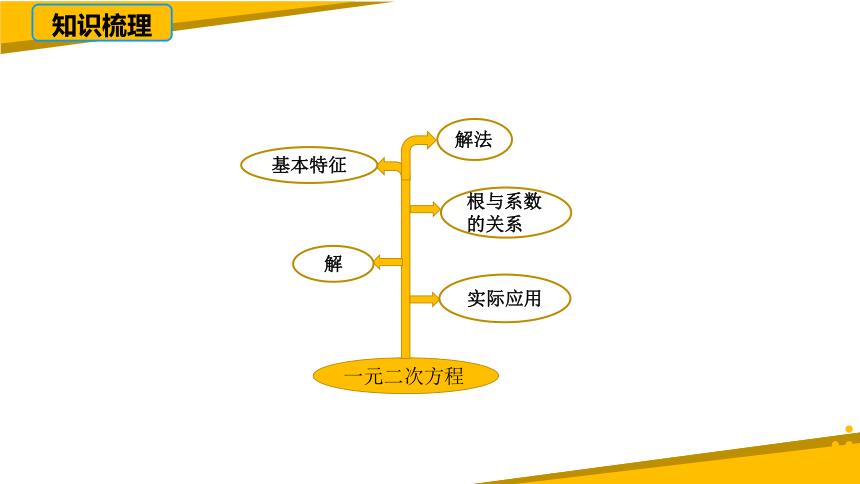
知识梳理
知识梳理
一元二次方程
根与系数的关系
基本特征
实际应用
解
解法
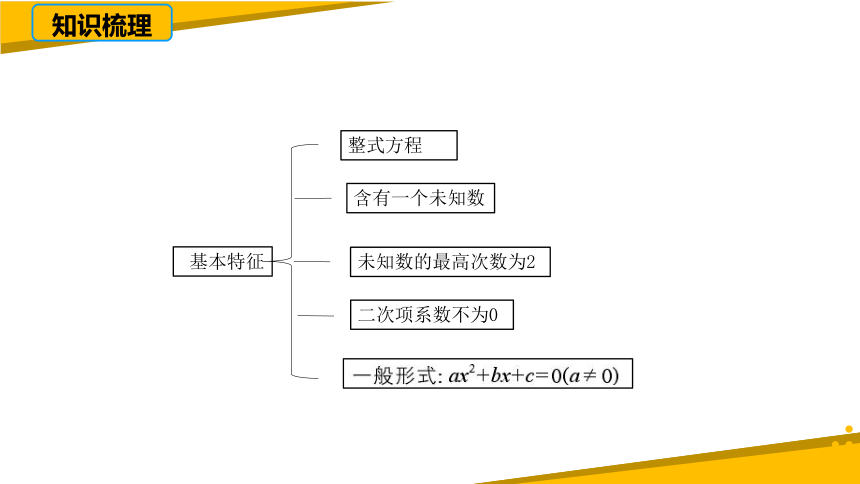
知识梳理
整式方程
含有一个未知数
未知数的最高次数为2
二次项系数不为0
基本特征
未知数的最高次数为2
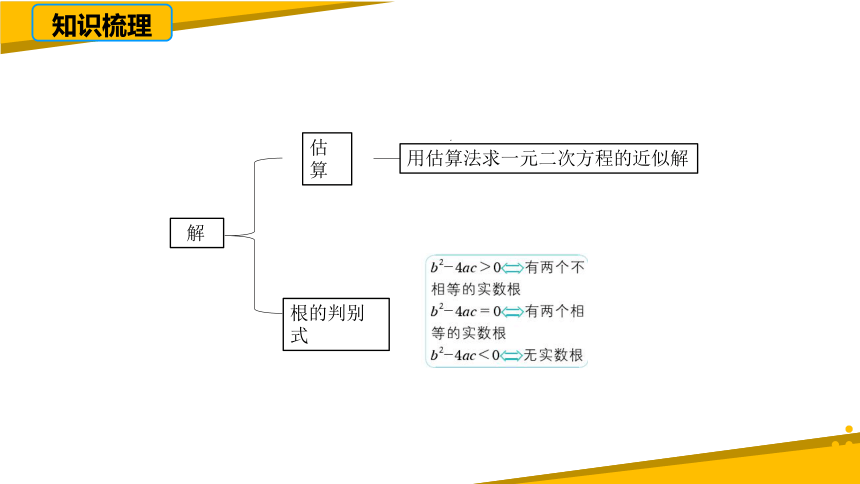
知识梳理
估算
根的判别式
解
用估算法求一元二次方程的近似解
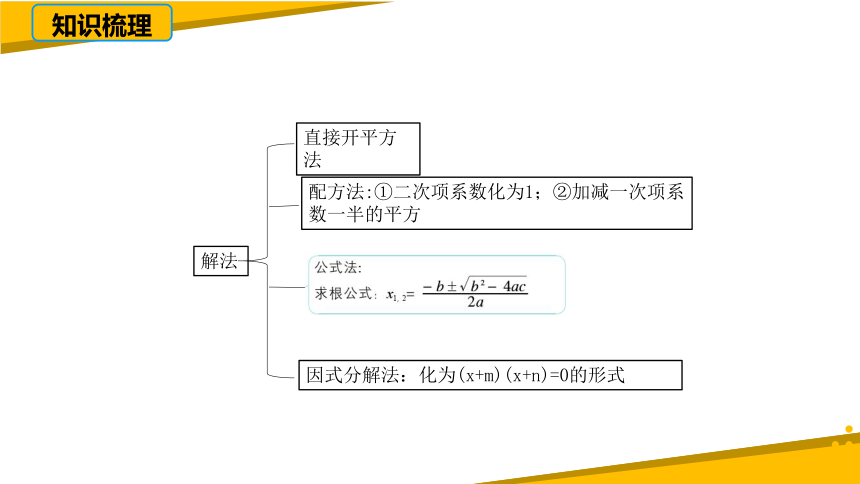
知识梳理
直接开平方法
配方法:①二次项系数化为1;②加减一次项系数一半的平方
解法
因式分解法:化为(x+m)(x+n)=0的形式
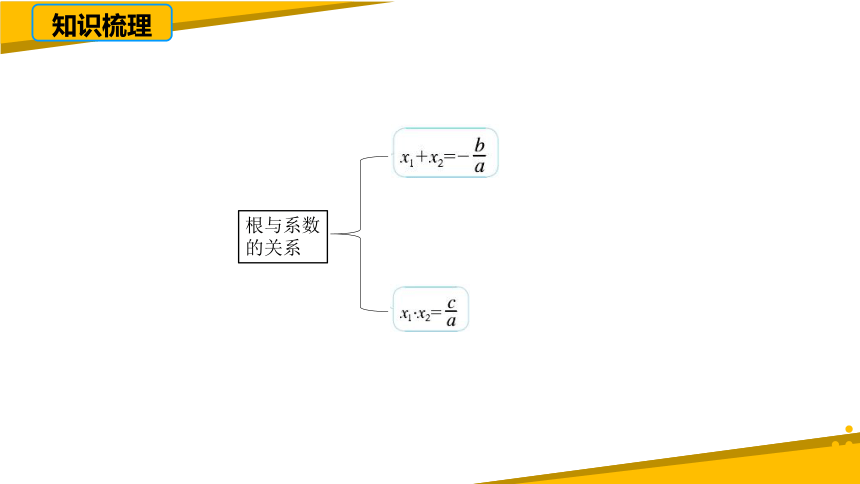
知识梳理
根与系数的关系
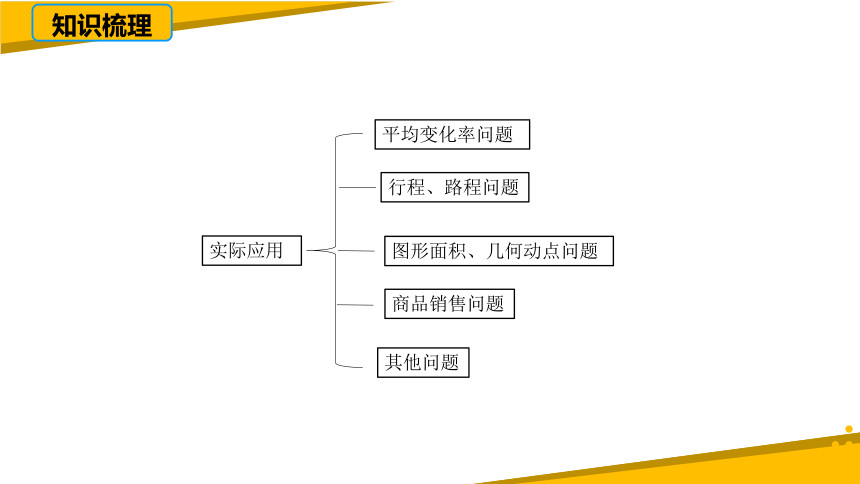
知识梳理
平均变化率问题
行程、路程问题
图形面积、几何动点问题
商品销售问题
实际应用
其他问题
知识梳理
一、一元二次方程的基本概念
1.定义:
只含有一个未知数的整式方程,并且都可以化为 ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一般形式:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
知识梳理
3.项数和系数:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
一次项: ax2 一次项系数:a
二次项: bx 二次项系数:b
常数项:c
4.注意事项:
(1)含有一个未知数; (2)未知数的最高次数为2;
(3)二次项系数不为0; (4)整式方程.
知识梳理
二、解一元二次方程的方法
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
x2 + px + q = 0 (p2 - 4q ≥0)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) (x + n)=0
各种一元二次方程的解法及使用类型
知识梳理
三、一元二次方程在生活中的应用
列方程解应用题的一般步骤:
审
设
列
解
检
答
(1)审题:通过审题弄清已知量与未知量之间的数量关系.
(2)设元:就是设未知数,分直接设与间接设,应根据实际需要恰当选取设元法.
(3)列方程:就是建立已知量与未知量之间的等量关系.列方程这一环节最重要,决定着能否顺利解决实际问题.
(4)解方程:正确求出方程的解并注意检验其合理性.
(5)作答:即写出答语,遵循问什么答什么的原则写清答语.
典例解析
考点一 一元二次方程的定义
例1 若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A. m≠1 B. m=1 C. m≥1 D. m≠0
解析 本题考查了一元二次方程的定义,即方程中必须保证有二次项(二次项系数不为0),因此它的系数m-1≠0,即m≠1,故选A.
A
1.方程5x2-x-3=x2-3+x的二次项系数是 ,一次项系数是 ,常数项是 .
4
-2
0
针对训练
典例解析
考点二 一元二次方程的根的应用
解析 根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等,故只要把x=0代入就可以得到以m为未知数的方程m2-1=0,解得m=±1的值.这里应填-1.这种题的解题方法我们称之为“有根必代”.
例2 若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
-1
典例解析
针对训练
2. 一元二次方程x2+px-2=0的一个根为2,则p的值为 _______.
-1
3.若关于x的一元二次方程 ax +bx+5=0(a≠0)的一个解是x=1, 则2018-a-b的值是__.
2023
典例解析
【易错提示】(1)配方法的前提是二次项系数是1;(a-b)2与(a+b)2 要准确区分;(2)求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否成三角形的好习惯
解析 (1)配方法的关键是配上一次项系数一半的平方;
(2)先求出方程x2﹣13x+36=0的两根,再根据三角形的三边关系定理,得到符合题意的边,进而求得三角形周长.
考点三 一元二次方程的解法
例3 (1)用配方法解方程x2-2x-5=0时,原方程应变为( )
A. (x-1)2=6 B.(x+2)2=9
C. (x+1)2=6 D.(x-2)2=9
(2) (易错题)三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的根,则该三角形的周长为( )
A.13 B. 15 C.18 D.13或18
A
A
典例解析
4.菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
A. 16 B. 12 C. 16或12 D. 24
A
针对训练
典例解析
5.用公式法和配方法分别解方程:x2-4x-1=0
(要求写出必要解题步骤).
典例解析
考点四 一元二次方程的根的判别式的应用
例4 已知关于x的一元二次方程x2-3m=4x有两个不相等的实数根,则m的取值范围是( )
A. B. m<2 C. m ≥0 D. m<0
A
解析 根据方程根的情况可知,此方程的根的判别式 >0,即42-4×1×(-3m)=16+12m>0,解得 ,故选A.
Δ
典例解析
6.下列所给方程中,没有实数根的是( )
A. x2+x=0 B. 5x2-4x-1=0
C.3x2-4x+1=0 D. 4x2-5x+2=0
7.(开放题)若关于x的一元二次方程x2-x+m=0有两个不相等的实数根,则m的值可能是 (写出一个即可).
D
0
针对训练
典例解析
考点五 一元二次方程的根与系数的关系
例5 已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= .
25
解析 根据根与系数的关系可知,m+n=4,mn=-3. m2-mn+n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25.
【重要变形】
典例解析
针对训练
8. 已知方程2x2+4x-3=0的两根分别为x1和x2,则x12+x22的值等于( )
A. 7 B. -2 C. D.
A
典例解析
几何问题
例6 如图1,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540平方米,求道路的宽.
图1
解析 本题利用图形的变换——平移,把零散的图形面积集中化,再建立方程并求解.
考点六 一元二次方程的应用
典例解析
解:设道路宽为x米,由平移得到图2,则宽为(20-x)米,长为(32-x)米,列方程得
(20-x)(32-x)=540,
整理得 x2-52x+100=0.
解得 x1=50(舍去),x2=2.
答:道路宽为2米.
图2
图1
典例解析
解决有关面积问题时,除了对所学图形面积公式熟悉外,还要会将不规则图形分割或组合成规则图形,并找出各部分图形面积之间的关系,再列方程求解.
(注意:这里的横坚斜小路的的宽度都相等)
平移转化
方法总结
典例解析
例7 某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.
(1)若公司每天的销售价为x元,则每天的销售量为多少?
(2)如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
市场销售问题
典例解析
解析 本题为销售中的利润问题,其基本本数量关系用表析分如下:设公司每天的销售价为x元.
单件利润 销售量(件) 每星期利润(元)
正常销售
涨价销售
4
32
x-20
32-2(x-24)
150
其等量关系是:总利润=单件利润×销售量.
解:(1)32-(x-24) ×2=80-2x;
(2)由题意可得(x-20)(80-2x)=150.
解得 x1=25, x2=35.
由题意x≤28, ∴x=25,即售价应当为25元.
【易错提示】销售量在正常销售的基础上进行减少.要注意验根.
128
典例解析
例8 菜农小王种植的某种蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该种蔬菜滞销.小王为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.求平均每次下调的百分率是多少?
解:设平均每次下调的百分率是x,根据题意得
5(1-x)2=3.2
解得 x1=1.8 (舍去), x2=0.2=20%.
答:平均每次下调的百分率是20%.
平均变化率问题
典例解析
9. (易错题)要在一块长52米,宽48米的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
52
48
x
x
图①
小亮设计的方案如图①所示,甬面宽度均为xm,剩下四块绿地面种共2300m2.
小颖设计的方案如图②所示,BC=HE=xm,AB∥CD,HG∥EF,AB ⊥EF, ∠1=60 °.
x
x
G
F
H
E
A
D
(
1
B
C
图②
52
48
针对训练
典例解析
解:(1)根据小亮的设计方案列方程,得(52-x)(48-x)=2300.
解得x1=2,x2=98(不合题意,舍去).
答:小亮设计方案中甬路的宽度为2m;
(2)在图2中作AI⊥CD,HJ⊥EF,垂足分别是为I,J.
∵AB ∥CD, ∴四边形ADCB是平行四边形.
由(1)得x=2, ∴AD=BC=HE=2m.
在Rt △ADI中, ∠ADC=∠1=60 °,
AD=2m,
∴AI= m,同理HJ= m.
∴小颖设计方案中四块绿地的总面
积=52 ×48-2 ×52-2×48+ =2299(m2).
x
x
G
F
H
E
A
D
(
1
B
C
图②
52
48
J
I
典例解析
10.小明对某水果批发市场某种水果销售情况调查发现:如果每千克赢利10元, 每天可售出500千克. 对市场进一步调查发现, 在进价不变的 情况下, 若每千克这种水果在原售价的基础上每涨价1元, 则日销售量将减 少20千克. 如果市场某天销售这种水果赢利6000元, 同时顾客又得到了实惠, 那么该天每千克这种水果涨价多少元?
典例解析
分析 根据“销售利润=销售的千克数×每千克的利润”构建方程.
解 设该天每千克这种水果涨价x元, 由题意得
(10+x)(500-20x)=6000,
整理, 得x -15x+50=0, 解得 x1 =5, x2 =10.
因为顾客得到了实惠, 所以应取x=5.
答:该天每千克这种水果涨价5元.
典例解析
11.某养殖户每年的养殖成本 包括固定成本和可变成本, 其中固定成本每年均为4万 元, 可变成本逐年增长, 已 知该养殖户第1年的可变成 本为2.6万元, 设可变成本平 均每年增长的百分率为x.(1)用含x的代数式表示第3 年的可变成本为万元;
(2)如果该养殖户第3年的养 殖成本为7.146万元, 求可变成本平均每年增长的百分率x.
典例解析
中考链接
A
2019
课堂小结
一元二次方程
一元二次方
程的定义
概念:①整式方程; ②一元; ③二次.
一般形式:ax2+bx+c=0 (a≠0)
一元二次方程的解法
直接开平方法
配方法
公式法
因式分解法
根的判别式及
根与系数的关系
根的判别式: Δ=b2-4ac
根与系数的关系
一元二次方程的应用
营销问题、平均变化率问题
几何问题、数字问题
当堂测试
D
D
C
当堂测试
当堂测试
5.选用合适的方法求解一元二次方程
分层作业
B
A
【基础达标作业】
分层作业
4.已知关于x的方程(2k+1)x2+4kx+k-1=0,问:
(1)k为何值时,此方程是一元一次方程?
(2)k为何值时,此方程是一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数及常数项.
【能力提升作业】
分层作业
【拓展延伸作业】
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十一章一元二次方程小结
学习目标
1)了解一元二次方程及其相关概念,会用配方法、公式法、分解因式法解一元二次方程,并在解一元二次方程的过程中体会转换、降次等数学思想。
2)通过根的判别式判断一元二次方程的情况,了解根与系数的关系。
3)能够利用一元二次方程解决有关实际问题,能根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力。
知识梳理
知识梳理
一元二次方程
根与系数的关系
基本特征
实际应用
解
解法
知识梳理
整式方程
含有一个未知数
未知数的最高次数为2
二次项系数不为0
基本特征
未知数的最高次数为2
知识梳理
估算
根的判别式
解
用估算法求一元二次方程的近似解
知识梳理
直接开平方法
配方法:①二次项系数化为1;②加减一次项系数一半的平方
解法
因式分解法:化为(x+m)(x+n)=0的形式
知识梳理
根与系数的关系
知识梳理
平均变化率问题
行程、路程问题
图形面积、几何动点问题
商品销售问题
实际应用
其他问题
知识梳理
一、一元二次方程的基本概念
1.定义:
只含有一个未知数的整式方程,并且都可以化为 ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一般形式:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
知识梳理
3.项数和系数:
ax2 + bx +c=0 (a,b,c为常数,a≠0)
一次项: ax2 一次项系数:a
二次项: bx 二次项系数:b
常数项:c
4.注意事项:
(1)含有一个未知数; (2)未知数的最高次数为2;
(3)二次项系数不为0; (4)整式方程.
知识梳理
二、解一元二次方程的方法
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
x2 + px + q = 0 (p2 - 4q ≥0)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) (x + n)=0
各种一元二次方程的解法及使用类型
知识梳理
三、一元二次方程在生活中的应用
列方程解应用题的一般步骤:
审
设
列
解
检
答
(1)审题:通过审题弄清已知量与未知量之间的数量关系.
(2)设元:就是设未知数,分直接设与间接设,应根据实际需要恰当选取设元法.
(3)列方程:就是建立已知量与未知量之间的等量关系.列方程这一环节最重要,决定着能否顺利解决实际问题.
(4)解方程:正确求出方程的解并注意检验其合理性.
(5)作答:即写出答语,遵循问什么答什么的原则写清答语.
典例解析
考点一 一元二次方程的定义
例1 若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A. m≠1 B. m=1 C. m≥1 D. m≠0
解析 本题考查了一元二次方程的定义,即方程中必须保证有二次项(二次项系数不为0),因此它的系数m-1≠0,即m≠1,故选A.
A
1.方程5x2-x-3=x2-3+x的二次项系数是 ,一次项系数是 ,常数项是 .
4
-2
0
针对训练
典例解析
考点二 一元二次方程的根的应用
解析 根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等,故只要把x=0代入就可以得到以m为未知数的方程m2-1=0,解得m=±1的值.这里应填-1.这种题的解题方法我们称之为“有根必代”.
例2 若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
-1
典例解析
针对训练
2. 一元二次方程x2+px-2=0的一个根为2,则p的值为 _______.
-1
3.若关于x的一元二次方程 ax +bx+5=0(a≠0)的一个解是x=1, 则2018-a-b的值是__.
2023
典例解析
【易错提示】(1)配方法的前提是二次项系数是1;(a-b)2与(a+b)2 要准确区分;(2)求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否成三角形的好习惯
解析 (1)配方法的关键是配上一次项系数一半的平方;
(2)先求出方程x2﹣13x+36=0的两根,再根据三角形的三边关系定理,得到符合题意的边,进而求得三角形周长.
考点三 一元二次方程的解法
例3 (1)用配方法解方程x2-2x-5=0时,原方程应变为( )
A. (x-1)2=6 B.(x+2)2=9
C. (x+1)2=6 D.(x-2)2=9
(2) (易错题)三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的根,则该三角形的周长为( )
A.13 B. 15 C.18 D.13或18
A
A
典例解析
4.菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
A. 16 B. 12 C. 16或12 D. 24
A
针对训练
典例解析
5.用公式法和配方法分别解方程:x2-4x-1=0
(要求写出必要解题步骤).
典例解析
考点四 一元二次方程的根的判别式的应用
例4 已知关于x的一元二次方程x2-3m=4x有两个不相等的实数根,则m的取值范围是( )
A. B. m<2 C. m ≥0 D. m<0
A
解析 根据方程根的情况可知,此方程的根的判别式 >0,即42-4×1×(-3m)=16+12m>0,解得 ,故选A.
Δ
典例解析
6.下列所给方程中,没有实数根的是( )
A. x2+x=0 B. 5x2-4x-1=0
C.3x2-4x+1=0 D. 4x2-5x+2=0
7.(开放题)若关于x的一元二次方程x2-x+m=0有两个不相等的实数根,则m的值可能是 (写出一个即可).
D
0
针对训练
典例解析
考点五 一元二次方程的根与系数的关系
例5 已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= .
25
解析 根据根与系数的关系可知,m+n=4,mn=-3. m2-mn+n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.故填25.
【重要变形】
典例解析
针对训练
8. 已知方程2x2+4x-3=0的两根分别为x1和x2,则x12+x22的值等于( )
A. 7 B. -2 C. D.
A
典例解析
几何问题
例6 如图1,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540平方米,求道路的宽.
图1
解析 本题利用图形的变换——平移,把零散的图形面积集中化,再建立方程并求解.
考点六 一元二次方程的应用
典例解析
解:设道路宽为x米,由平移得到图2,则宽为(20-x)米,长为(32-x)米,列方程得
(20-x)(32-x)=540,
整理得 x2-52x+100=0.
解得 x1=50(舍去),x2=2.
答:道路宽为2米.
图2
图1
典例解析
解决有关面积问题时,除了对所学图形面积公式熟悉外,还要会将不规则图形分割或组合成规则图形,并找出各部分图形面积之间的关系,再列方程求解.
(注意:这里的横坚斜小路的的宽度都相等)
平移转化
方法总结
典例解析
例7 某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.
(1)若公司每天的销售价为x元,则每天的销售量为多少?
(2)如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?
市场销售问题
典例解析
解析 本题为销售中的利润问题,其基本本数量关系用表析分如下:设公司每天的销售价为x元.
单件利润 销售量(件) 每星期利润(元)
正常销售
涨价销售
4
32
x-20
32-2(x-24)
150
其等量关系是:总利润=单件利润×销售量.
解:(1)32-(x-24) ×2=80-2x;
(2)由题意可得(x-20)(80-2x)=150.
解得 x1=25, x2=35.
由题意x≤28, ∴x=25,即售价应当为25元.
【易错提示】销售量在正常销售的基础上进行减少.要注意验根.
128
典例解析
例8 菜农小王种植的某种蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该种蔬菜滞销.小王为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.求平均每次下调的百分率是多少?
解:设平均每次下调的百分率是x,根据题意得
5(1-x)2=3.2
解得 x1=1.8 (舍去), x2=0.2=20%.
答:平均每次下调的百分率是20%.
平均变化率问题
典例解析
9. (易错题)要在一块长52米,宽48米的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
52
48
x
x
图①
小亮设计的方案如图①所示,甬面宽度均为xm,剩下四块绿地面种共2300m2.
小颖设计的方案如图②所示,BC=HE=xm,AB∥CD,HG∥EF,AB ⊥EF, ∠1=60 °.
x
x
G
F
H
E
A
D
(
1
B
C
图②
52
48
针对训练
典例解析
解:(1)根据小亮的设计方案列方程,得(52-x)(48-x)=2300.
解得x1=2,x2=98(不合题意,舍去).
答:小亮设计方案中甬路的宽度为2m;
(2)在图2中作AI⊥CD,HJ⊥EF,垂足分别是为I,J.
∵AB ∥CD, ∴四边形ADCB是平行四边形.
由(1)得x=2, ∴AD=BC=HE=2m.
在Rt △ADI中, ∠ADC=∠1=60 °,
AD=2m,
∴AI= m,同理HJ= m.
∴小颖设计方案中四块绿地的总面
积=52 ×48-2 ×52-2×48+ =2299(m2).
x
x
G
F
H
E
A
D
(
1
B
C
图②
52
48
J
I
典例解析
10.小明对某水果批发市场某种水果销售情况调查发现:如果每千克赢利10元, 每天可售出500千克. 对市场进一步调查发现, 在进价不变的 情况下, 若每千克这种水果在原售价的基础上每涨价1元, 则日销售量将减 少20千克. 如果市场某天销售这种水果赢利6000元, 同时顾客又得到了实惠, 那么该天每千克这种水果涨价多少元?
典例解析
分析 根据“销售利润=销售的千克数×每千克的利润”构建方程.
解 设该天每千克这种水果涨价x元, 由题意得
(10+x)(500-20x)=6000,
整理, 得x -15x+50=0, 解得 x1 =5, x2 =10.
因为顾客得到了实惠, 所以应取x=5.
答:该天每千克这种水果涨价5元.
典例解析
11.某养殖户每年的养殖成本 包括固定成本和可变成本, 其中固定成本每年均为4万 元, 可变成本逐年增长, 已 知该养殖户第1年的可变成 本为2.6万元, 设可变成本平 均每年增长的百分率为x.(1)用含x的代数式表示第3 年的可变成本为万元;
(2)如果该养殖户第3年的养 殖成本为7.146万元, 求可变成本平均每年增长的百分率x.
典例解析
中考链接
A
2019
课堂小结
一元二次方程
一元二次方
程的定义
概念:①整式方程; ②一元; ③二次.
一般形式:ax2+bx+c=0 (a≠0)
一元二次方程的解法
直接开平方法
配方法
公式法
因式分解法
根的判别式及
根与系数的关系
根的判别式: Δ=b2-4ac
根与系数的关系
一元二次方程的应用
营销问题、平均变化率问题
几何问题、数字问题
当堂测试
D
D
C
当堂测试
当堂测试
5.选用合适的方法求解一元二次方程
分层作业
B
A
【基础达标作业】
分层作业
4.已知关于x的方程(2k+1)x2+4kx+k-1=0,问:
(1)k为何值时,此方程是一元一次方程?
(2)k为何值时,此方程是一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数及常数项.
【能力提升作业】
分层作业
【拓展延伸作业】
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
