第五章 二元一次方程组 学案(无答案) 2023—2024学年北师大版数学八年级上册
文档属性
| 名称 | 第五章 二元一次方程组 学案(无答案) 2023—2024学年北师大版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 303.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 00:00:00 | ||
图片预览


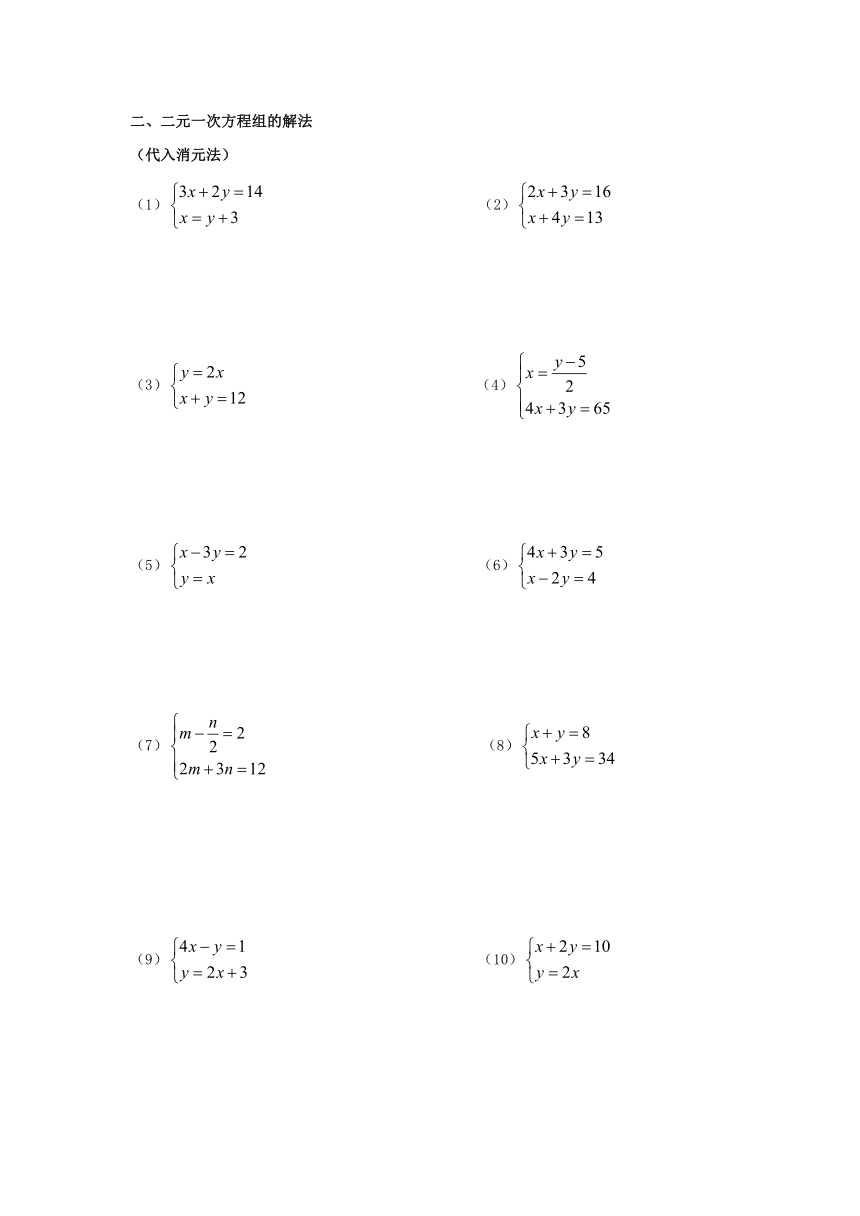

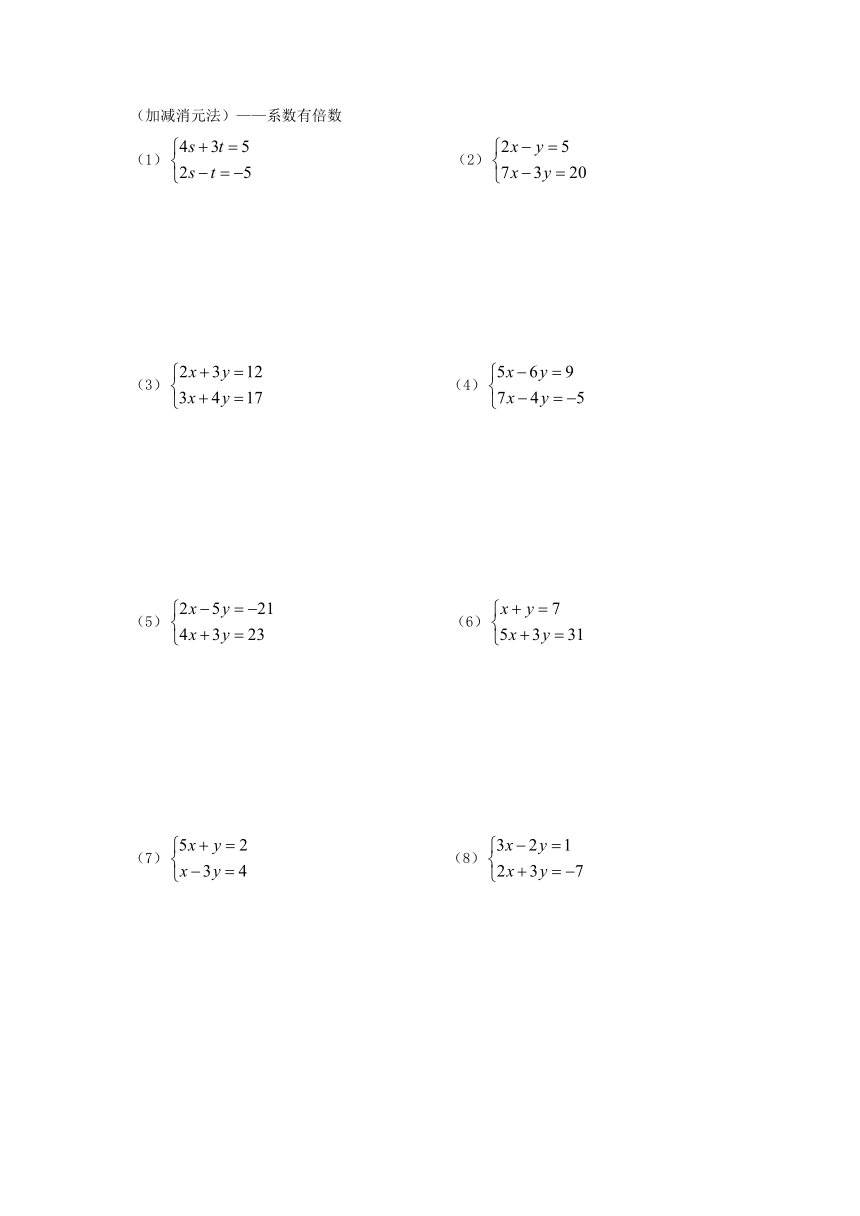
文档简介
二元一次方程组
定义
①含有 个未知数,并且所含未知数的项的次数都是 的方程叫做二元一次方程
1.下列等式:①2x+y=4;②3xy=7;③x2+2y=0;④2=y;⑤2x+y+z=1,是二元一次方程的是
2.若ax+4y=3x﹣7是关于x,y的二元一次方程,则a的取值范围是( )
A.a≠﹣2 B.a≠0 C.a≠3 D.a≠﹣1
②使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的 ;
二元一次方程的解有 个
若 是关于的方程的解,则 .
已知是关于x、y的方程ax+by=3的一组解,则2a+4b﹣1的值为
3.下面4组数值中,哪些是二元一次方程2x+y=10的解?
A. B. C. D.
③二元一次方程的整数解
1.二元一次方程2x+3y=8有多少个正整数解?( )
A.0个 B.1个 C.2个 D.3个
2.如果是方程2ax+by=13的解,a,b是正整数,则a+b的最小值是( )
A.3 B.4 C.5 D.6
3.方程2x+3y=24共有 组非负整数解.
④共含有 个未知数的两个一次方程组成的一组方程,叫做二元一次方程组
1.下列方程组中,不是二元一次方程组的是( ).
A. B. C. D.
2.在方程组,,,, 中,是二元一次方程组的有( )
A.2个 B.3个 C.4个 D.5个
⑤二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解
二元一次方程组的解通常有 个
1.以 为解的二元一次方程组是( ).
A. B. C. D.
2.二元一次方程组的解是( )
A. B. C. D.
3.二元一次方程组的解是( )
A. B. C. D.
4.在(1)(2)(3)(4)中, 是方程7x﹣3y=2的解; 是方程2x+y=8的解; 是方程组的解.
5.已知甲种物品每个重4kg,乙种物品每个重7kg,现有甲种物品x个,乙种物品y个,共重76kg.
(1)列出关于x,y的二元一次方程;
(2)若x=12,则y= .
(3)若乙种物品有8个,则甲种物品有 个.
6.小明和小丽两人同时到一家水果店买水果.小明买了1kg苹果和2kg梨,共花了26元;小丽买了2kg苹果和1kg梨,共花了28元.苹果和梨的价格各为多少?
根据题意,小明列出方程组:.
而小丽列出的是:.
交流后,他们发现两个方程组不同,于是展开了争论,都说自己是正确的,而对方是错误的.他们列的方程组正确吗?你认为他们产生分歧的原因是什么?
二元一次方程组的解法
(代入消元法)
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
(加减消元法)
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
(加减消元法)——系数有倍数
(1) (2)
(3) (4)
(5) (6)
(7) (8)
自选方法解下列方程组:
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
专题一 ——方程组的解
1.如果是方程x﹣3y=﹣3的一组解,那么5﹣a+3b=
2.关于x、y的二元一次方程3x﹣ay=1有一个解是,则a= .
3.已知,都是方程ax﹣y=b的解,则a= ,b= .
4. 若二元一次方程组的解为,则a+b等于 .
5.已知x,y满足方程组,则x+y的值为
6.若方程组的解满足x+y=0,则k的值为 .
7.关于x,y的二元一次方程组的解满足x﹣y=3,则m=
8.已知关于x,y的二元一次方程组的解为,则a﹣2b的值是 .
9.如果方程组的解与方程组的解相同,则a+b的值为
10.若方程组与方程组的解相同,则a= ,b= .
11.如果二元一次方程组的解是二元一次方程3x﹣5y﹣7=0的一个解,那么a值是
12.若关于x、y的二元一次方程组的解是,则关于a、b的二元一次方程组的解是 .
13.已知方程组的解是,则的解是
14.(1)解二元一次方程组
(2)可以用哪些方法得到方程组的解,并对这些方法进行比较.
应用题——整数解
1.把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有( )
A.3种 B.4种 C.5种 D.9种
2.某学校计划用17件同样的奖品全部用于奖励在“扫黑除恶宣传”活动中表现突出的班级,一等奖奖励3件,二等奖奖励2件,则分配一、二等奖个数的方案有( )
A.1种 B.2种 C.3种 D.4种
3.为了开展“阳光体育”活动,某班计划购买甲、乙两种体育用品(每种体育用品都购买),其中甲种体育用品每件20元,乙种体育用品每件30元,共用去150元,请你设计一下,共有 种购买方案.
4.学校计划购买A和B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元.学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
5.为奖励消防演练活动中表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,在购买资金恰好用尽的情况下,购买方案有( )
A.4种 B.3种 C.2种 D.1种
6.在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A、B、C三种奖品,A种每个10元,B种每个20元,C种每个30元,在C种奖品不超过两个且钱全部用完的情况下,有多少种购买方案( )
A.12种 B.15种 C.16种 D.14种
应用题——鸡兔同笼
1、今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何
2.今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?
3.100个和尚分100个馒头,大和尚1人分3个馒头,小和尚3人分1个馒头,问大小和尚各有多少人?
4.在美国职业篮球联赛中,我国著名篮球运动员姚明在一次比赛中22投14中得22分,若他投中了2个三分球,则他还投中了几个两分球和几个罚球?(罚球投中一次记1分)
5.《孙子算经》中记载了一道题,大意是100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可列方程组为 .
6.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为
7.小明从邮局买了面值50分和80分的邮票共9枚,花了6.3元.小明买了两种邮票各多少枚?
8.某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有x人,绘画小组有y人,那么可列方程组为( )
A. B. C. D.
9.小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为
10.医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要
11.某商店准备用两种价格分别为36元/kg和20元/kg的糖果混合成杂拌糖果出售,混合后糖果的价格是28元/kg.现在要配制这种杂拌糖果100kg,需要两种糖果各多少千克?
12.某校有两种类型的学生宿舍30间,大的宿舍每间可住8人,小的每间可住5人,该校198个住宿生恰好住满这30间宿舍.大小宿舍各有多少间?
13.某旅馆的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天35元,一个50人的旅游团到该旅馆住宿,租住了若干客房,且每个客房正好住满,一天共花去住宿费1510元,两种客房各租住了多少间?
14.某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 黄瓜 茄子
批发价/(元/kg) 2.4 2
零售价/(元/kg) 3.6 2.8
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
15.某景点的门票价格如下:
购票人数/人 1﹣50 51﹣100 100人以上
每人门票价/元 12 10 8
我校八年级(1)(2)两个班共102人去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.如果两班都以班级为单位分别购票.则一共应付1116元;如果两班联合起来作为一个团体购票,则可以节省不少钱,两班各有多少名学生?联合起来购票能省多少钱?
应用题——绳长测井
以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
2.用一根绳子围绕一个大树,若环绕大树3周,绳子还多4尺;若环绕大树4周,绳子少了3尺。这根绳子有多长?环绕大树一周需要多少尺?
3.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )
A. B. C. D.
4.我国古代数学著作记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,方程组( )
A. B. C. D.
应用题——盈不足
将一摞笔记本分给若干同学.每个同学5本,则剩下8本;每个同学8本,又差了7本,共有多少本笔记本,多少个同学?
2.有几个人一起买一件物品,每人出8元多3元;每人出7元少4元.问有多少人?该物品价值多少元?
3.小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下多少元?
4.《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为x,买鸡钱数为y,方程组为( )
A. B. C. D.
5.我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )
A. B. C. D.=
应用题——增收节支
问题1:增长(亏损)率问题的公式:
某工厂去年的利润(总产值-总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元
2.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.问甲、乙两种商品原来的单价分别为多少元?
3.某粮食生产专业户去年计划生产水稻和小麦共15吨,实际生产了17吨,其中水稻超产15%,小麦超产10%,该专业户去年计划生产水稻、小麦各多少吨?
4.某商店将某种碳酸饮料每瓶的价格下调了10%.将某种果汁饮料每瓶的价格上调了5%,已知调价前买这两种饮料各一瓶共花费8元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费19.8元,若设上述碳酸饮料、果汁饮料在调价前每瓶分别为x元和y元,则可列方程组为____________________
5.某果园现有桃树和杏树共500棵,计划一年后桃树增加3%,杏树增加4%,这样果园里这两种果树将增加3.6%,如果设该果园现有桃树和杏树分别为x棵,y棵,可列方程组为_____
__________
6.我市某九年一贯制学校共有学生3000人,计划一年后初中在校生增加8%,小学在校生增加11%,这样全校在校生将增加10%,设这所学校现初中在校生x人,小学在校生y人,由题意可列方程组为____________________
问题2:打折公式
1.某商场购进商品后,加价40%作为销售价,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元.两种商品原销售价之和为490元.则两种商品进价分别为多少元?
2.某商场按定价销售某种商品时,每件可获利45元;按定价的八五折销售该商品8件与将定价降低35元销售该商品12件所获利润相等,该商品进价、定价分别是多少?
3.某商场购进甲、乙两种商品后,甲种商品加价50%、乙种商品加价40%作为标价,适逢元旦,商场举办促销活动,甲种商品打八折销售,乙种商品打八五折销售,某顾客购买甲、乙两种商品各1件,共付款538元,已知商场共盈利88元,求甲、乙两种商品的进价各是多少元.
4.甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后,两种商品的单价和比原来的单价和提高了20%.问甲、乙两种商品原来的单价各是多少元?
5.某公司用3000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,两种货物共获利315元,如果设该公司购进这两种货物所用的费用分别为x元,y元,则列出的方程组是____________________
其他百分比问题:
1.为了研究吸烟是否对肺癌有影响,某研究所随机地抽查了1000人.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这1000人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,可列出的方程组是____________________
2.一二两班共有100名学生,他们的体育达标率为81%.如果一班学生体育达标率为87.5%,二班学生体育达标率为75%,那么一二班各有多少名学生?
3.有甲乙两种溶液,甲种溶液由酒精1升,水3升配制而成;乙种溶液由酒精3升,水2升配制而成.现要配制浓度为50%的酒精溶液7升,甲乙两种溶液应各取几升
4.甲、乙两种盐水,若分别取甲种盐水240g,乙种盐水120g,混合后,制成的盐水浓度为8%;若分别取甲种盐水80g,乙种盐水160g,混合后,制成的盐水浓度为10%,求甲、乙两种盐水的浓度各是多少?如果设甲种盐水的浓度为x,乙种盐水浓度为y,根据题意,可列出方程组是___________________
应用题——数字问题
热身准备:
一个两位数的十位数字是x,个位数字是y,则这个两位数可表示为_________
如果交换个位和十位上的数字,那么得到一个新的两位数可表示为_________
2. 一个三位数,若百位数字为a,十位数字为b,个位数字为c,则这个三位数为:__________.
3. 两位数x放在两位数y的左边,组成一个四位数,因此用x,y表示这个四位数为________.如果将x放在y的右边,那么得到一个新的四位数为___________.
4. 一个两位数,个位上的数是m,十位上的数是n,如果在它们之间添上零,那么用代数式表示这个三位数为_______.
列方程组解应用题:
一个两位数,个位上的数字与十位上的数字之和是11,如果把十位上的数字与个位上的数字对调,那么所得的两位数比原两位数大9,求原来的两位数.
两个两位数的和为 68,在较大的两位数的右边接着写较小的两位数,得到一个四位数; 在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2 178, 求这两个两位数.
3.小明和小亮做加法游戏,小明在一个加数后面多写了一个0,得到的和为242;而小亮在另一个加数后面多写了一个0,得到的和为341.设原来的两个加数分别为x,y,请列出满足题意的方程组 .
4.一个两位数是另一个两位数的3倍,如果把这个两位数放在另一个两位数的左边与放在右边所得的数之和为8484.求这个两位数.
5.一个两位数,个位数比十位数大2,若把各位数字和十位数字对调,则所得的新的两位数比原数的两倍少17.若设原数的个位数为x,十位数字为y,则可列方程组为?
6.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
有大小两个两位数,在大数的右边写上一个0之后再写上小的数,得到一个五位数;在小数的右边写上大数,然后再写上一个0,也得到一个五位数,第一个五位数除以第二个五位数得到的商为2,余数为590.此外,二倍大数与三倍小数的和是72,求这两个两位数.
应用题——行程问题
1.李刚骑摩托车在公路上匀速行驶,早晨7:00时看到里程碑上的数是一个两位数,它的数字之和是9;8:00时看里程碑上的两位数与7:00时看到的个位数和十位数互换了;9:00时看到里程碑上的数是7:00时看到的数的8倍,李刚在7:00时看到的数是?
2.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程表上的数如下:则12:00看到的两位数是 .
时刻 12:00 13:00 14:30
里程表上 的数 是一个两位数,数字之和为6 十位与个位数字与12:00时所看到的正好颠倒了 比12:00时看到的两位数中间多了个0
甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人速度各是多少
4. 甲、乙两人赛跑,若乙先跑10米,甲跑5秒即可追上乙;若乙先跑2秒,则甲跑4秒就可追上乙.设甲速为x米/秒,乙速为y米/秒,则可列方程组为?
5.甲、乙两人匀速在400米环形跑道上跑步,同时同地出发,如果相向而行,每隔1分钟相遇一次;如果同向而行,每隔5分钟相遇一次,已知甲比乙的速度快.设甲每分钟跑x米,乙每分钟跑y米,根据题意,列出方程组正确的是( )
A. B. C. D.
6.某体育场环形跑道长400米,甲乙分别以一定的速度练习长跑和自行车。如果反向而行,那么他们每隔30秒相遇一次;如果同向而行,那么每隔80秒乙就追上甲一次。甲乙速度分别是多少?
7.甲、乙两地相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
8.小颖家离学校1880 m,其中有一段为上坡路 ,另一段为下坡路,她跑步去学校共用了16 min .已知小颖在上坡时的平均速度是 4.8 km/h,下坡时的平均速度是12 km/h.问小颖上、下坡各用了多长时间?
9.汽车在上坡时速度为28km/h,下坡时速度42km/h,从甲地到乙地用了4小时30分,返回时用了4小时40分,从甲地到乙地上、下坡路各是多少千米?
10.A,B两地相距80km,一艘船从A出发,顺水航行4h到B,而从B出发逆水航行5h到A,已知船顺水航行、逆水航行的速度分别是船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流速度.
应用题——配套问题
现用160张铁皮做盒子,每张铁皮做6个盒身或做20个盒底,而一个盒身与两个盒底配 成一个盒子,设用x张铁皮做盒身,y张铁皮做盒底,使盒底与盒身正好配套.则可列方程组为 .
某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组 .
3.某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子1张或椅子4把,现计划用120块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,则可列方程组 .
4.某生产车间共90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使1个螺栓配套2个螺帽,应如何分配工人才能使每天生产的螺栓和螺帽刚好配套,设生产螺栓x人,生产螺帽y人,可列方程组 .
5.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,若设需安排x名工人加工大齿轮,y名工人加工小齿轮,则根据题意可得方程组 .
6.要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分x张做侧面,另一部分y张做底面.已知每张白卡纸可以做侧面4个,或做底面6个,如果4个侧面可以和2个底面做成一个包装盒.可列方程组为 .
7. 用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)分别求裁剪出的侧面和底面的个数(用x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
应用题——驮包裹
1.老牛:“累死我了!”
小马:“你还累?这么大的个儿,才比我多驮了2个.”
老牛:“哼,我从你背上拿来1个,我的包裹数就是你的2倍!”
小马:…
根据老牛和小马的对话,你能用列方程求出它们各驮了多少个包裹吗?
2.《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意可列方程组为 .
3.《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?
4.10年前,小明妈妈的年龄是小明的6倍;10年后,小明妈妈的年龄是小明的2倍,小明和他妈妈现在的年龄分别是多少?
5.已知甲乙两人年收入之比为3:2,年支出之比为7:4,年终时两人各余400元,则甲的年收入为 元,乙的年支出为 元。
6.《九章算术》书中有这样的一个问题:五只雀,六只燕共重一斤,雀重燕轻,互换一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )
A. B. C. D.
应用题——图形中找等量关系
1.八块相同的长方形地砖拼成一个长方形,每块长方形地砖的宽等于 ,面积为
2.如图,由8个大小相同的小长方形无缝拼接而成的的一个大长方形,已知大长方形的周长为40cm,则小长方形的周长为 cm.
3.如图,周长为68cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为 cm2.
4.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是 ;阴影部分的面积之和为 .
5.在长为20m、宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则每个小长方形花圃的面积是 m2.
6.将如图左侧所示的6个大小、形状完全相同的小长方形放置在右侧的大长方形中,所标尺寸如图所示(单位:cm),则图中含有阴影部分的总面积为 cm2.
7.如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积.
8.利用两块长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是
9.如图,有四个相同的小长方形和两个相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是
10.如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案,已知A(﹣2,6),则点B的坐标为
11.如图是由截面为同一种矩形的墙砖粘贴的墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,每块墙砖的截面面积是 .
一次函数与方程组的关系
1.解答下列问题.
(1)方程x+y=5的解有多少个?请写出几个;
在坐标系中描出以这些解为坐标的点,它们在一次函数 的图象上
(2)方程2x﹣y=4的解有多少个?请写出几个;
在坐标系中描出以这些解为坐标的点,它们在一次函数 的图象上
直接写出二元一次方程组的解
两条直线的交点坐标与该方程组的解有什么关系?
2.已知一次函数y=3x﹣1与y=2x的图象的交点是(1,2).求方程组的解.
3.已知方程组的解是,试求直线y=3x﹣3与y=﹣x+3交点的坐标.
4.已知直线y=2x与y=﹣x+b的交点为(1,a),确定方程组的解和a、b的值.
5.已知一次函数y=3x﹣5与y=2x+b的图象的交点的坐标为P(1,﹣2).
求方程组的解和b的值.
6.在同一坐标系中画出一次函数和的图象,直线和直线的交点是 ,方程组的解是
7.已知一次函数y=kx﹣b(k、b为常数,且k≠0,b≠0)与y=x的图象相交于点M(a,1),则关于x的方程(k﹣)x=b的解为x= .
8.图中的两条直线,l1,l2的交点坐标可以看做方程组 的解.
9.如图,直线l1,l2的交点坐标可以看做方程组 的解.
10.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,关于x的方程x+5=ax+b的解是( )
A.x=20 B.x=25 C.x=20或25 D.x=﹣20
11.如图,函数y=kx+b(k≠0)的图象经过点B(3,0),与函数y=2x的图象交于点A,则关于x的方程kx+b=2x的解为
12.如图,一次函数y=﹣2x和y=kx+b的图象相交于点A(m,3),则关于x的方程kx+b+2x=0的解为 .
13.一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程组的解为( )
A. B. C. D.
14.如图,直线y=kx(k≠0)与y=x+4在第二象限交于A,y=x+4交x轴,y轴分别于B、C两点.S△ABO:S△ACO=1:2,则方程组的解为
15.(1)在同一平面直角坐标系中,一次函数y=x+1和y=x﹣2的图象(如图)有怎样的位置关系?方程组解的情况如何?你发现了什么?
16.方程组解的情况是 ,则一次函数y=2﹣2x与y=5﹣2x图象之间的位置关系是 .
定义
①含有 个未知数,并且所含未知数的项的次数都是 的方程叫做二元一次方程
1.下列等式:①2x+y=4;②3xy=7;③x2+2y=0;④2=y;⑤2x+y+z=1,是二元一次方程的是
2.若ax+4y=3x﹣7是关于x,y的二元一次方程,则a的取值范围是( )
A.a≠﹣2 B.a≠0 C.a≠3 D.a≠﹣1
②使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的 ;
二元一次方程的解有 个
若 是关于的方程的解,则 .
已知是关于x、y的方程ax+by=3的一组解,则2a+4b﹣1的值为
3.下面4组数值中,哪些是二元一次方程2x+y=10的解?
A. B. C. D.
③二元一次方程的整数解
1.二元一次方程2x+3y=8有多少个正整数解?( )
A.0个 B.1个 C.2个 D.3个
2.如果是方程2ax+by=13的解,a,b是正整数,则a+b的最小值是( )
A.3 B.4 C.5 D.6
3.方程2x+3y=24共有 组非负整数解.
④共含有 个未知数的两个一次方程组成的一组方程,叫做二元一次方程组
1.下列方程组中,不是二元一次方程组的是( ).
A. B. C. D.
2.在方程组,,,, 中,是二元一次方程组的有( )
A.2个 B.3个 C.4个 D.5个
⑤二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解
二元一次方程组的解通常有 个
1.以 为解的二元一次方程组是( ).
A. B. C. D.
2.二元一次方程组的解是( )
A. B. C. D.
3.二元一次方程组的解是( )
A. B. C. D.
4.在(1)(2)(3)(4)中, 是方程7x﹣3y=2的解; 是方程2x+y=8的解; 是方程组的解.
5.已知甲种物品每个重4kg,乙种物品每个重7kg,现有甲种物品x个,乙种物品y个,共重76kg.
(1)列出关于x,y的二元一次方程;
(2)若x=12,则y= .
(3)若乙种物品有8个,则甲种物品有 个.
6.小明和小丽两人同时到一家水果店买水果.小明买了1kg苹果和2kg梨,共花了26元;小丽买了2kg苹果和1kg梨,共花了28元.苹果和梨的价格各为多少?
根据题意,小明列出方程组:.
而小丽列出的是:.
交流后,他们发现两个方程组不同,于是展开了争论,都说自己是正确的,而对方是错误的.他们列的方程组正确吗?你认为他们产生分歧的原因是什么?
二元一次方程组的解法
(代入消元法)
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
(加减消元法)
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
(加减消元法)——系数有倍数
(1) (2)
(3) (4)
(5) (6)
(7) (8)
自选方法解下列方程组:
(1) (2)
(3) (4)
(5) (6)
(7) (8)
(9) (10)
专题一 ——方程组的解
1.如果是方程x﹣3y=﹣3的一组解,那么5﹣a+3b=
2.关于x、y的二元一次方程3x﹣ay=1有一个解是,则a= .
3.已知,都是方程ax﹣y=b的解,则a= ,b= .
4. 若二元一次方程组的解为,则a+b等于 .
5.已知x,y满足方程组,则x+y的值为
6.若方程组的解满足x+y=0,则k的值为 .
7.关于x,y的二元一次方程组的解满足x﹣y=3,则m=
8.已知关于x,y的二元一次方程组的解为,则a﹣2b的值是 .
9.如果方程组的解与方程组的解相同,则a+b的值为
10.若方程组与方程组的解相同,则a= ,b= .
11.如果二元一次方程组的解是二元一次方程3x﹣5y﹣7=0的一个解,那么a值是
12.若关于x、y的二元一次方程组的解是,则关于a、b的二元一次方程组的解是 .
13.已知方程组的解是,则的解是
14.(1)解二元一次方程组
(2)可以用哪些方法得到方程组的解,并对这些方法进行比较.
应用题——整数解
1.把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有( )
A.3种 B.4种 C.5种 D.9种
2.某学校计划用17件同样的奖品全部用于奖励在“扫黑除恶宣传”活动中表现突出的班级,一等奖奖励3件,二等奖奖励2件,则分配一、二等奖个数的方案有( )
A.1种 B.2种 C.3种 D.4种
3.为了开展“阳光体育”活动,某班计划购买甲、乙两种体育用品(每种体育用品都购买),其中甲种体育用品每件20元,乙种体育用品每件30元,共用去150元,请你设计一下,共有 种购买方案.
4.学校计划购买A和B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元.学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
5.为奖励消防演练活动中表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,在购买资金恰好用尽的情况下,购买方案有( )
A.4种 B.3种 C.2种 D.1种
6.在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A、B、C三种奖品,A种每个10元,B种每个20元,C种每个30元,在C种奖品不超过两个且钱全部用完的情况下,有多少种购买方案( )
A.12种 B.15种 C.16种 D.14种
应用题——鸡兔同笼
1、今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何
2.今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?
3.100个和尚分100个馒头,大和尚1人分3个馒头,小和尚3人分1个馒头,问大小和尚各有多少人?
4.在美国职业篮球联赛中,我国著名篮球运动员姚明在一次比赛中22投14中得22分,若他投中了2个三分球,则他还投中了几个两分球和几个罚球?(罚球投中一次记1分)
5.《孙子算经》中记载了一道题,大意是100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可列方程组为 .
6.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为
7.小明从邮局买了面值50分和80分的邮票共9枚,花了6.3元.小明买了两种邮票各多少枚?
8.某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有x人,绘画小组有y人,那么可列方程组为( )
A. B. C. D.
9.小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为
10.医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要
11.某商店准备用两种价格分别为36元/kg和20元/kg的糖果混合成杂拌糖果出售,混合后糖果的价格是28元/kg.现在要配制这种杂拌糖果100kg,需要两种糖果各多少千克?
12.某校有两种类型的学生宿舍30间,大的宿舍每间可住8人,小的每间可住5人,该校198个住宿生恰好住满这30间宿舍.大小宿舍各有多少间?
13.某旅馆的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天35元,一个50人的旅游团到该旅馆住宿,租住了若干客房,且每个客房正好住满,一天共花去住宿费1510元,两种客房各租住了多少间?
14.某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 黄瓜 茄子
批发价/(元/kg) 2.4 2
零售价/(元/kg) 3.6 2.8
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
15.某景点的门票价格如下:
购票人数/人 1﹣50 51﹣100 100人以上
每人门票价/元 12 10 8
我校八年级(1)(2)两个班共102人去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.如果两班都以班级为单位分别购票.则一共应付1116元;如果两班联合起来作为一个团体购票,则可以节省不少钱,两班各有多少名学生?联合起来购票能省多少钱?
应用题——绳长测井
以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
2.用一根绳子围绕一个大树,若环绕大树3周,绳子还多4尺;若环绕大树4周,绳子少了3尺。这根绳子有多长?环绕大树一周需要多少尺?
3.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )
A. B. C. D.
4.我国古代数学著作记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,方程组( )
A. B. C. D.
应用题——盈不足
将一摞笔记本分给若干同学.每个同学5本,则剩下8本;每个同学8本,又差了7本,共有多少本笔记本,多少个同学?
2.有几个人一起买一件物品,每人出8元多3元;每人出7元少4元.问有多少人?该物品价值多少元?
3.小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下多少元?
4.《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为x,买鸡钱数为y,方程组为( )
A. B. C. D.
5.我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )
A. B. C. D.=
应用题——增收节支
问题1:增长(亏损)率问题的公式:
某工厂去年的利润(总产值-总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元
2.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.问甲、乙两种商品原来的单价分别为多少元?
3.某粮食生产专业户去年计划生产水稻和小麦共15吨,实际生产了17吨,其中水稻超产15%,小麦超产10%,该专业户去年计划生产水稻、小麦各多少吨?
4.某商店将某种碳酸饮料每瓶的价格下调了10%.将某种果汁饮料每瓶的价格上调了5%,已知调价前买这两种饮料各一瓶共花费8元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费19.8元,若设上述碳酸饮料、果汁饮料在调价前每瓶分别为x元和y元,则可列方程组为____________________
5.某果园现有桃树和杏树共500棵,计划一年后桃树增加3%,杏树增加4%,这样果园里这两种果树将增加3.6%,如果设该果园现有桃树和杏树分别为x棵,y棵,可列方程组为_____
__________
6.我市某九年一贯制学校共有学生3000人,计划一年后初中在校生增加8%,小学在校生增加11%,这样全校在校生将增加10%,设这所学校现初中在校生x人,小学在校生y人,由题意可列方程组为____________________
问题2:打折公式
1.某商场购进商品后,加价40%作为销售价,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元.两种商品原销售价之和为490元.则两种商品进价分别为多少元?
2.某商场按定价销售某种商品时,每件可获利45元;按定价的八五折销售该商品8件与将定价降低35元销售该商品12件所获利润相等,该商品进价、定价分别是多少?
3.某商场购进甲、乙两种商品后,甲种商品加价50%、乙种商品加价40%作为标价,适逢元旦,商场举办促销活动,甲种商品打八折销售,乙种商品打八五折销售,某顾客购买甲、乙两种商品各1件,共付款538元,已知商场共盈利88元,求甲、乙两种商品的进价各是多少元.
4.甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后,两种商品的单价和比原来的单价和提高了20%.问甲、乙两种商品原来的单价各是多少元?
5.某公司用3000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,两种货物共获利315元,如果设该公司购进这两种货物所用的费用分别为x元,y元,则列出的方程组是____________________
其他百分比问题:
1.为了研究吸烟是否对肺癌有影响,某研究所随机地抽查了1000人.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这1000人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,可列出的方程组是____________________
2.一二两班共有100名学生,他们的体育达标率为81%.如果一班学生体育达标率为87.5%,二班学生体育达标率为75%,那么一二班各有多少名学生?
3.有甲乙两种溶液,甲种溶液由酒精1升,水3升配制而成;乙种溶液由酒精3升,水2升配制而成.现要配制浓度为50%的酒精溶液7升,甲乙两种溶液应各取几升
4.甲、乙两种盐水,若分别取甲种盐水240g,乙种盐水120g,混合后,制成的盐水浓度为8%;若分别取甲种盐水80g,乙种盐水160g,混合后,制成的盐水浓度为10%,求甲、乙两种盐水的浓度各是多少?如果设甲种盐水的浓度为x,乙种盐水浓度为y,根据题意,可列出方程组是___________________
应用题——数字问题
热身准备:
一个两位数的十位数字是x,个位数字是y,则这个两位数可表示为_________
如果交换个位和十位上的数字,那么得到一个新的两位数可表示为_________
2. 一个三位数,若百位数字为a,十位数字为b,个位数字为c,则这个三位数为:__________.
3. 两位数x放在两位数y的左边,组成一个四位数,因此用x,y表示这个四位数为________.如果将x放在y的右边,那么得到一个新的四位数为___________.
4. 一个两位数,个位上的数是m,十位上的数是n,如果在它们之间添上零,那么用代数式表示这个三位数为_______.
列方程组解应用题:
一个两位数,个位上的数字与十位上的数字之和是11,如果把十位上的数字与个位上的数字对调,那么所得的两位数比原两位数大9,求原来的两位数.
两个两位数的和为 68,在较大的两位数的右边接着写较小的两位数,得到一个四位数; 在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2 178, 求这两个两位数.
3.小明和小亮做加法游戏,小明在一个加数后面多写了一个0,得到的和为242;而小亮在另一个加数后面多写了一个0,得到的和为341.设原来的两个加数分别为x,y,请列出满足题意的方程组 .
4.一个两位数是另一个两位数的3倍,如果把这个两位数放在另一个两位数的左边与放在右边所得的数之和为8484.求这个两位数.
5.一个两位数,个位数比十位数大2,若把各位数字和十位数字对调,则所得的新的两位数比原数的两倍少17.若设原数的个位数为x,十位数字为y,则可列方程组为?
6.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字之和,商是5,余数是1.这个两位数是多少?
有大小两个两位数,在大数的右边写上一个0之后再写上小的数,得到一个五位数;在小数的右边写上大数,然后再写上一个0,也得到一个五位数,第一个五位数除以第二个五位数得到的商为2,余数为590.此外,二倍大数与三倍小数的和是72,求这两个两位数.
应用题——行程问题
1.李刚骑摩托车在公路上匀速行驶,早晨7:00时看到里程碑上的数是一个两位数,它的数字之和是9;8:00时看里程碑上的两位数与7:00时看到的个位数和十位数互换了;9:00时看到里程碑上的数是7:00时看到的数的8倍,李刚在7:00时看到的数是?
2.小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程表上的数如下:则12:00看到的两位数是 .
时刻 12:00 13:00 14:30
里程表上 的数 是一个两位数,数字之和为6 十位与个位数字与12:00时所看到的正好颠倒了 比12:00时看到的两位数中间多了个0
甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇,甲、乙两人速度各是多少
4. 甲、乙两人赛跑,若乙先跑10米,甲跑5秒即可追上乙;若乙先跑2秒,则甲跑4秒就可追上乙.设甲速为x米/秒,乙速为y米/秒,则可列方程组为?
5.甲、乙两人匀速在400米环形跑道上跑步,同时同地出发,如果相向而行,每隔1分钟相遇一次;如果同向而行,每隔5分钟相遇一次,已知甲比乙的速度快.设甲每分钟跑x米,乙每分钟跑y米,根据题意,列出方程组正确的是( )
A. B. C. D.
6.某体育场环形跑道长400米,甲乙分别以一定的速度练习长跑和自行车。如果反向而行,那么他们每隔30秒相遇一次;如果同向而行,那么每隔80秒乙就追上甲一次。甲乙速度分别是多少?
7.甲、乙两地相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
8.小颖家离学校1880 m,其中有一段为上坡路 ,另一段为下坡路,她跑步去学校共用了16 min .已知小颖在上坡时的平均速度是 4.8 km/h,下坡时的平均速度是12 km/h.问小颖上、下坡各用了多长时间?
9.汽车在上坡时速度为28km/h,下坡时速度42km/h,从甲地到乙地用了4小时30分,返回时用了4小时40分,从甲地到乙地上、下坡路各是多少千米?
10.A,B两地相距80km,一艘船从A出发,顺水航行4h到B,而从B出发逆水航行5h到A,已知船顺水航行、逆水航行的速度分别是船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流速度.
应用题——配套问题
现用160张铁皮做盒子,每张铁皮做6个盒身或做20个盒底,而一个盒身与两个盒底配 成一个盒子,设用x张铁皮做盒身,y张铁皮做盒底,使盒底与盒身正好配套.则可列方程组为 .
某车间有60名工人生产太阳镜,1名工人每天可生产镜片200片或镜架50个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排x名工人生产镜片,y名工人生产镜架,则可列方程组 .
3.某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子1张或椅子4把,现计划用120块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,则可列方程组 .
4.某生产车间共90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使1个螺栓配套2个螺帽,应如何分配工人才能使每天生产的螺栓和螺帽刚好配套,设生产螺栓x人,生产螺帽y人,可列方程组 .
5.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,若设需安排x名工人加工大齿轮,y名工人加工小齿轮,则根据题意可得方程组 .
6.要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分x张做侧面,另一部分y张做底面.已知每张白卡纸可以做侧面4个,或做底面6个,如果4个侧面可以和2个底面做成一个包装盒.可列方程组为 .
7. 用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)分别求裁剪出的侧面和底面的个数(用x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
应用题——驮包裹
1.老牛:“累死我了!”
小马:“你还累?这么大的个儿,才比我多驮了2个.”
老牛:“哼,我从你背上拿来1个,我的包裹数就是你的2倍!”
小马:…
根据老牛和小马的对话,你能用列方程求出它们各驮了多少个包裹吗?
2.《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意可列方程组为 .
3.《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?
4.10年前,小明妈妈的年龄是小明的6倍;10年后,小明妈妈的年龄是小明的2倍,小明和他妈妈现在的年龄分别是多少?
5.已知甲乙两人年收入之比为3:2,年支出之比为7:4,年终时两人各余400元,则甲的年收入为 元,乙的年支出为 元。
6.《九章算术》书中有这样的一个问题:五只雀,六只燕共重一斤,雀重燕轻,互换一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )
A. B. C. D.
应用题——图形中找等量关系
1.八块相同的长方形地砖拼成一个长方形,每块长方形地砖的宽等于 ,面积为
2.如图,由8个大小相同的小长方形无缝拼接而成的的一个大长方形,已知大长方形的周长为40cm,则小长方形的周长为 cm.
3.如图,周长为68cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为 cm2.
4.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是 ;阴影部分的面积之和为 .
5.在长为20m、宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则每个小长方形花圃的面积是 m2.
6.将如图左侧所示的6个大小、形状完全相同的小长方形放置在右侧的大长方形中,所标尺寸如图所示(单位:cm),则图中含有阴影部分的总面积为 cm2.
7.如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积.
8.利用两块长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是
9.如图,有四个相同的小长方形和两个相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是
10.如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案,已知A(﹣2,6),则点B的坐标为
11.如图是由截面为同一种矩形的墙砖粘贴的墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,每块墙砖的截面面积是 .
一次函数与方程组的关系
1.解答下列问题.
(1)方程x+y=5的解有多少个?请写出几个;
在坐标系中描出以这些解为坐标的点,它们在一次函数 的图象上
(2)方程2x﹣y=4的解有多少个?请写出几个;
在坐标系中描出以这些解为坐标的点,它们在一次函数 的图象上
直接写出二元一次方程组的解
两条直线的交点坐标与该方程组的解有什么关系?
2.已知一次函数y=3x﹣1与y=2x的图象的交点是(1,2).求方程组的解.
3.已知方程组的解是,试求直线y=3x﹣3与y=﹣x+3交点的坐标.
4.已知直线y=2x与y=﹣x+b的交点为(1,a),确定方程组的解和a、b的值.
5.已知一次函数y=3x﹣5与y=2x+b的图象的交点的坐标为P(1,﹣2).
求方程组的解和b的值.
6.在同一坐标系中画出一次函数和的图象,直线和直线的交点是 ,方程组的解是
7.已知一次函数y=kx﹣b(k、b为常数,且k≠0,b≠0)与y=x的图象相交于点M(a,1),则关于x的方程(k﹣)x=b的解为x= .
8.图中的两条直线,l1,l2的交点坐标可以看做方程组 的解.
9.如图,直线l1,l2的交点坐标可以看做方程组 的解.
10.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,关于x的方程x+5=ax+b的解是( )
A.x=20 B.x=25 C.x=20或25 D.x=﹣20
11.如图,函数y=kx+b(k≠0)的图象经过点B(3,0),与函数y=2x的图象交于点A,则关于x的方程kx+b=2x的解为
12.如图,一次函数y=﹣2x和y=kx+b的图象相交于点A(m,3),则关于x的方程kx+b+2x=0的解为 .
13.一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程组的解为( )
A. B. C. D.
14.如图,直线y=kx(k≠0)与y=x+4在第二象限交于A,y=x+4交x轴,y轴分别于B、C两点.S△ABO:S△ACO=1:2,则方程组的解为
15.(1)在同一平面直角坐标系中,一次函数y=x+1和y=x﹣2的图象(如图)有怎样的位置关系?方程组解的情况如何?你发现了什么?
16.方程组解的情况是 ,则一次函数y=2﹣2x与y=5﹣2x图象之间的位置关系是 .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
