1.1探索勾股定理 同步练习(无答案)北师大版八年级数学上册
文档属性
| 名称 | 1.1探索勾股定理 同步练习(无答案)北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 22:34:17 | ||
图片预览



文档简介
1.1探索勾股定理
一、选择题
1.在Rt△ABC中,∠C=90°,若BC﹣AC=2cm,AB=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在离电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长是( )
A. 6米 B. 7米 C. 8米 D. 9米
3.如图,在四边形 中,,,,.分别以点 , 为圆心,大于 长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 .若点 是 的中点,则 的长为( )
A. B. C. D.
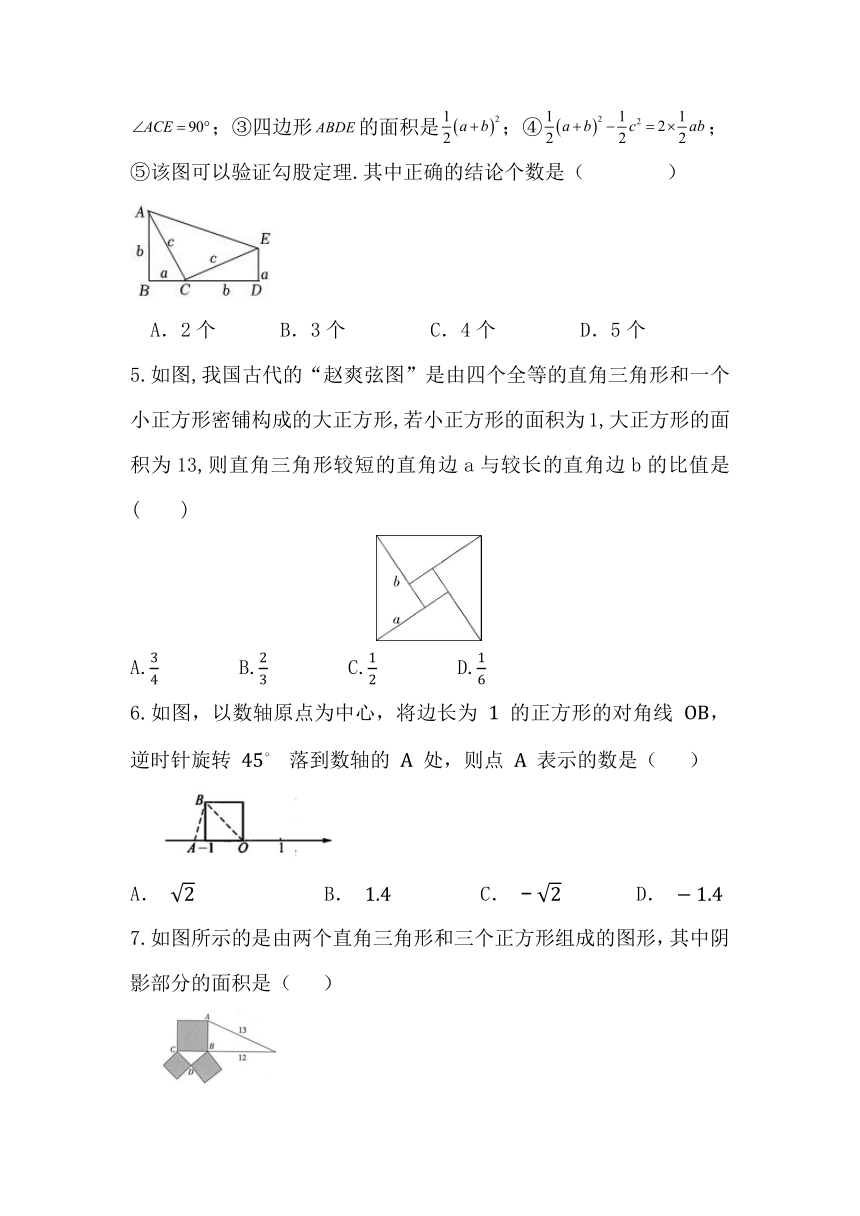
4.如图,在四边形中,//,,点是边上一点,,,.下列结论:①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
5.如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比值是( )
A. B. C. D.
6.如图,以数轴原点为中心,将边长为 的正方形的对角线 ,逆时针旋转 落到数轴的 处,则点 表示的数是( )
A. B. C. D.
7.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A. B. C. D.
8.如图,在四边形ABDE中,AB∥DE,AB⊥BD,点C是边BD上一点,BC=DE=a,CD=AB=b,AC=CE=c.下列结论:①△ABC≌△CDE;②∠ACE=90°;③四边形ABDE的面积是(a+b)2;④(a+b)2-c2=2×ab;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.5 B.4 C.3 D.2
9.如图,,且 ,,,则线段 的长为( )
A. B. C. D.
10.如图,中,,,.将折叠,使边落在边上,展开后得到折痕l,则l的长为( )
A. B. C.5 D.3
11.几千年来,在勾股定理的多种证明方法中,等面积法是典型的一种证法,清代数学家李锐运用这一方法借助三个正方形也证明了勾股定理如图,四边形ABCD,四边形DEFG,四边形CGHI均为正方形,EF交BG于点L,DG交IH于点K,点B,L,C,G在同一条直线上,若,,记四边形DELC的面积为,四边形CGKI的面积为,则的值为
A. B. C. D.
二、填空题
1.如图,在四边形ABCD中,,,,,连接BD,,,若P是BC边上一动点,则DP长的最小值为______.
2.如图,在四边形ABCD中,,,,则AD的取值范围是______.
3.如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为______.
4.勾股定理是初等几何中的一个基本定理.这个定理有十分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴趣,我国古代三国时期吴国的数学家赵爽创造的弦图,是最早证明勾股定理的方法,所谓弦图是指在正方形的每一边上各取一个点,再连接四点构成一个正方形,它可以验证勾股定理.在如图的弦图中,已知:正方形的顶点、、、分别在正方形的边、、、上.若正方形的面积,;则正方形的面积________.
5.如图所示的正方形网格中,每个小正方形的面积均为1,正方形ABCM,CDEN,MNPQ的顶点都在格点上,则正方形MNPQ的面积为 .
6.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图,若,,则图中阴影部分的面积为______.
7.在直线 上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是 ,,,正放置的四个正方形的面积依次是 ,,,,则 .
三、解答题
1.如图,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求:
(1)AO,FO的长;
(2)图中半圆的面积.
2.如图,在中,,,,点是外一点,连接,,且,.
求的长;
你能求出的度数吗?请试一试.
3.已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的倍,甲到达目的地C点的同时乙恰好到达终点D处.
(1)求tan∠ECD的值;
(2)求线段AB及BC的长度.
4.如图, 中,, 平分 , 于 ,若 ,,.
(1)求 的长.
(2)求 的面积.
5.已知 中,,,另有一块等腰直角三角板的直角顶点放在 处,,将三角板 绕点 旋转(点 在 内部),连接 ,,.
(1)求证:.
(2)当 时,求 的长.
6.如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边上距直角顶点米远的点处同时开始测量,点为终点.小娟沿的路径测得所经过的路程是米,小燕沿的路径测得所经过的路程也是米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由?
一、选择题
1.在Rt△ABC中,∠C=90°,若BC﹣AC=2cm,AB=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在离电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长是( )
A. 6米 B. 7米 C. 8米 D. 9米
3.如图,在四边形 中,,,,.分别以点 , 为圆心,大于 长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 .若点 是 的中点,则 的长为( )
A. B. C. D.
4.如图,在四边形中,//,,点是边上一点,,,.下列结论:①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
5.如图,我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形的面积为1,大正方形的面积为13,则直角三角形较短的直角边a与较长的直角边b的比值是( )
A. B. C. D.
6.如图,以数轴原点为中心,将边长为 的正方形的对角线 ,逆时针旋转 落到数轴的 处,则点 表示的数是( )
A. B. C. D.
7.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A. B. C. D.
8.如图,在四边形ABDE中,AB∥DE,AB⊥BD,点C是边BD上一点,BC=DE=a,CD=AB=b,AC=CE=c.下列结论:①△ABC≌△CDE;②∠ACE=90°;③四边形ABDE的面积是(a+b)2;④(a+b)2-c2=2×ab;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.5 B.4 C.3 D.2
9.如图,,且 ,,,则线段 的长为( )
A. B. C. D.
10.如图,中,,,.将折叠,使边落在边上,展开后得到折痕l,则l的长为( )
A. B. C.5 D.3
11.几千年来,在勾股定理的多种证明方法中,等面积法是典型的一种证法,清代数学家李锐运用这一方法借助三个正方形也证明了勾股定理如图,四边形ABCD,四边形DEFG,四边形CGHI均为正方形,EF交BG于点L,DG交IH于点K,点B,L,C,G在同一条直线上,若,,记四边形DELC的面积为,四边形CGKI的面积为,则的值为
A. B. C. D.
二、填空题
1.如图,在四边形ABCD中,,,,,连接BD,,,若P是BC边上一动点,则DP长的最小值为______.
2.如图,在四边形ABCD中,,,,则AD的取值范围是______.
3.如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为______.
4.勾股定理是初等几何中的一个基本定理.这个定理有十分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴趣,我国古代三国时期吴国的数学家赵爽创造的弦图,是最早证明勾股定理的方法,所谓弦图是指在正方形的每一边上各取一个点,再连接四点构成一个正方形,它可以验证勾股定理.在如图的弦图中,已知:正方形的顶点、、、分别在正方形的边、、、上.若正方形的面积,;则正方形的面积________.
5.如图所示的正方形网格中,每个小正方形的面积均为1,正方形ABCM,CDEN,MNPQ的顶点都在格点上,则正方形MNPQ的面积为 .
6.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图,若,,则图中阴影部分的面积为______.
7.在直线 上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是 ,,,正放置的四个正方形的面积依次是 ,,,,则 .
三、解答题
1.如图,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求:
(1)AO,FO的长;
(2)图中半圆的面积.
2.如图,在中,,,,点是外一点,连接,,且,.
求的长;
你能求出的度数吗?请试一试.
3.已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的倍,甲到达目的地C点的同时乙恰好到达终点D处.
(1)求tan∠ECD的值;
(2)求线段AB及BC的长度.
4.如图, 中,, 平分 , 于 ,若 ,,.
(1)求 的长.
(2)求 的面积.
5.已知 中,,,另有一块等腰直角三角板的直角顶点放在 处,,将三角板 绕点 旋转(点 在 内部),连接 ,,.
(1)求证:.
(2)当 时,求 的长.
6.如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边上距直角顶点米远的点处同时开始测量,点为终点.小娟沿的路径测得所经过的路程是米,小燕沿的路径测得所经过的路程也是米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
