14.3.1提公因式法课件
文档属性
| 名称 | 14.3.1提公因式法课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 649.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-21 00:00:00 | ||
图片预览




文档简介
课件16张PPT。14.3.1提 公 因 式 法你们是优秀的,我们就是快乐的。阅读教材114----115页,思考下列问题:
⑴把下列多项式写成整式的积的形式:
x2 +x=__________,x2 -1=__________,ma+mb+mc=______________.
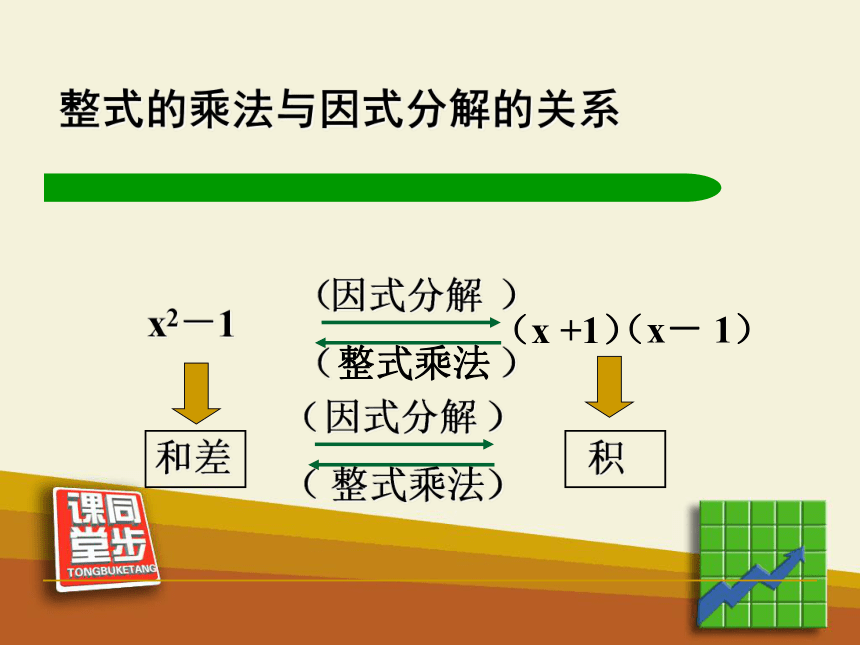
⑵把一个__________化成几个_________的形式,这种变形叫做把这个多项式因式分解(或分解因式).多项式x( x+1)( x+1)( x-1)m(a+b+c) 整式的积整式乘法 因式分解整式的乘法与因式分解的关系 因式分解整式乘法( )( )( )和差积( )x2-1(x +1)(x- 1)( )( )( )( )( )×√√××判断下列变形是不是因式分解活动1:理解提公因式法的意义
(一)如何确定公因式
2、多项式a2-a各项的公因式是____;
多项式10ab2 -5 ab3c 各项的公因式是________. 【合作探究】m公因式a5ab2 我们把多项式各项都含有的相同因式,叫做这个多项式各项的公因式.1、请同学们观察多项式:ma+mb+mc 它的各项都含有一个公共的因式______,我们把因式m叫做这个多项式各项的 . 如何找公因式?
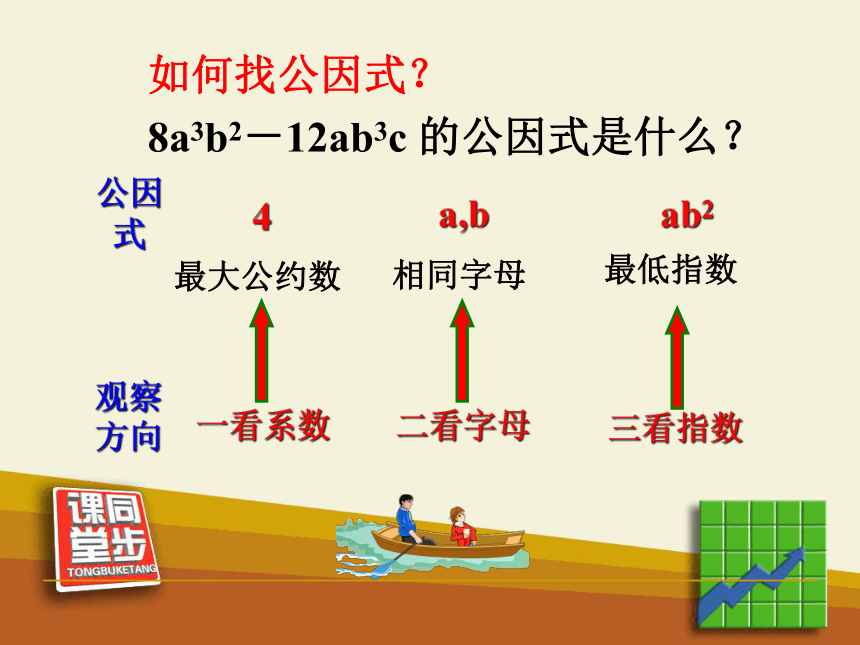
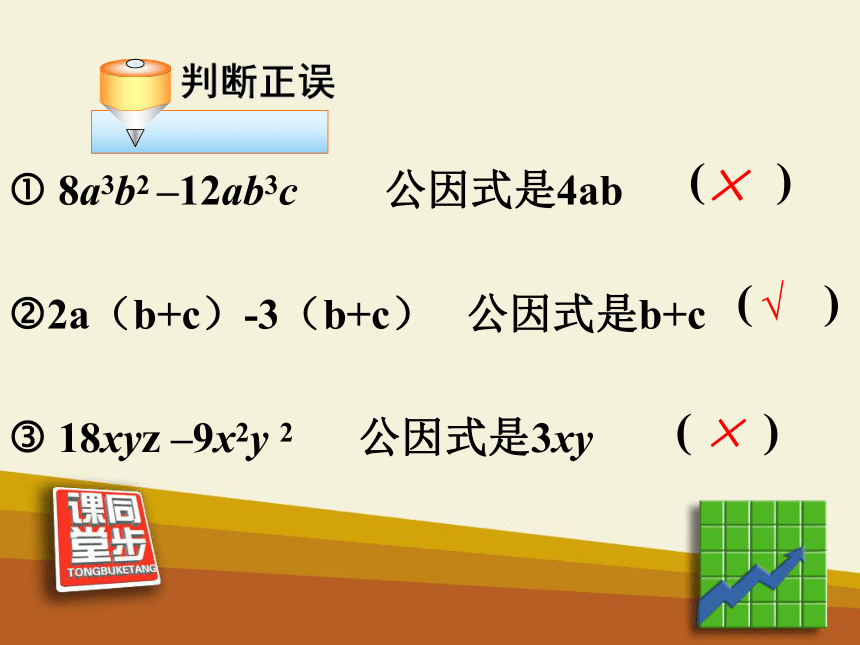
8a3b2-12ab3c 的公因式是什么?最大公约数相同字母公因式4a,bab2一看系数 观察方向二看字母三看指数最低指数? 8a3b2 –12ab3c 公因式是4ab
?2a(b+c)-3(b+c) 公因式是b+c
? 18xyz –9x2y 2 公因式是3xy ×( )√×( )( )方法总结确定公因式一般采取 “三定”的策略:
一定系数 各项系数绝对值的____公约数;
二定字母 各项都含有的________;
三定指数 相同字母的最________次数。相同字母最大低跟踪训练一:
5、在括号内填出下列各多项式中各项的公因式:
(1) ma+mb ( )
(2) ( )
(3) x(x-2)-3(x-2) ( )
(4) 4(x-2)+3(2-x) ( )mx-22ax-2(二)理解提公因式法定义. 6、根据乘法的分配律,可得 m(a+b+c)=
_________ 思考:要得到多项式的因式分解形式,怎么办?逆
变形:ma+mb+mc=m( ___________) 这说明,
多项式各项都含有的公因式 可以提到括号外面.
这样就把ma+mb+mc分解成两个因式 的形式,其
中一个因式m是各项的 ,另一个因式(a+b+c)
是ma+mb+mc除以 所得的商,像这种分解因式
的方法叫做 。 ma+mb+mc积 m a+b+c提公因式法m公因式提公因式法 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.活动2:会用提公因式法分解因式例1:把8a3b2+12ab3c分解因式
例2 把 2a(b+c) -3(b+c)分解因式. 解: 8a3b2 +12ab3c
=4ab2·2a2+4ab2·3bc
=4ab2 (2a2+3bc )运用提公因式法分解因式一般分为“三步”
一定:确定 ,把多项式的各项写成含公 因式的 _____的式;
二提:把公因式提到 ______ 前面,余下的项写在_____内.
三检查:检查各项的__________是否提彻底.公因式积括号公因式括号解: 注意:首项为负数时,要先变号再提公因式。当某一项和公因式相同时,提公因式后剩余的项是1.-3a2b3 +6a3b2c +3a2b -3a2b3 +6a3b2c +3a2b
= -( 3a2b3 -6a3b2c -3a2b)
= -(3a2b·b2-3a2b·2abc-3a2b·1)
=-3a2b (b2-2abc -1) 例3 分解因式: 把下列多项式分解因式:
(1)12x2y+18xy2; (2)-x2+xy-xz;
(3)2x3+6x2+2x
现有甲、乙、丙三位同学各做一题,他们的解法如下:
你认为他们的解法正确吗?试说明理由。
甲同学:
解:12x2y+18xy2
=3xy(4x+6y)乙同学:
解:-x2+xy-xz
=-x(x+y-z)丙同学:
解:2x3+6x2+2x
=2x(x2+3x)找错误 1.分解因式?2.确定公因式的方法?
一定系数 二定字母 三定指数课堂小结3、提公因式法分解因式步骤(分三步):
第一步,定公因式;
第二步,提公因式;
第三步,检查公因式是否提彻底。4、用提公因式法分解因式应注意的问题:1、公因式提取要彻底;
2、首项为负先提负;
3、提取公因式莫漏1.作业: 一定;二提;
三检查。
⑴把下列多项式写成整式的积的形式:
x2 +x=__________,x2 -1=__________,ma+mb+mc=______________.
⑵把一个__________化成几个_________的形式,这种变形叫做把这个多项式因式分解(或分解因式).多项式x( x+1)( x+1)( x-1)m(a+b+c) 整式的积整式乘法 因式分解整式的乘法与因式分解的关系 因式分解整式乘法( )( )( )和差积( )x2-1(x +1)(x- 1)( )( )( )( )( )×√√××判断下列变形是不是因式分解活动1:理解提公因式法的意义
(一)如何确定公因式
2、多项式a2-a各项的公因式是____;
多项式10ab2 -5 ab3c 各项的公因式是________. 【合作探究】m公因式a5ab2 我们把多项式各项都含有的相同因式,叫做这个多项式各项的公因式.1、请同学们观察多项式:ma+mb+mc 它的各项都含有一个公共的因式______,我们把因式m叫做这个多项式各项的 . 如何找公因式?
8a3b2-12ab3c 的公因式是什么?最大公约数相同字母公因式4a,bab2一看系数 观察方向二看字母三看指数最低指数? 8a3b2 –12ab3c 公因式是4ab
?2a(b+c)-3(b+c) 公因式是b+c
? 18xyz –9x2y 2 公因式是3xy ×( )√×( )( )方法总结确定公因式一般采取 “三定”的策略:
一定系数 各项系数绝对值的____公约数;
二定字母 各项都含有的________;
三定指数 相同字母的最________次数。相同字母最大低跟踪训练一:
5、在括号内填出下列各多项式中各项的公因式:
(1) ma+mb ( )
(2) ( )
(3) x(x-2)-3(x-2) ( )
(4) 4(x-2)+3(2-x) ( )mx-22ax-2(二)理解提公因式法定义. 6、根据乘法的分配律,可得 m(a+b+c)=
_________ 思考:要得到多项式的因式分解形式,怎么办?逆
变形:ma+mb+mc=m( ___________) 这说明,
多项式各项都含有的公因式 可以提到括号外面.
这样就把ma+mb+mc分解成两个因式 的形式,其
中一个因式m是各项的 ,另一个因式(a+b+c)
是ma+mb+mc除以 所得的商,像这种分解因式
的方法叫做 。 ma+mb+mc积 m a+b+c提公因式法m公因式提公因式法 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.活动2:会用提公因式法分解因式例1:把8a3b2+12ab3c分解因式
例2 把 2a(b+c) -3(b+c)分解因式. 解: 8a3b2 +12ab3c
=4ab2·2a2+4ab2·3bc
=4ab2 (2a2+3bc )运用提公因式法分解因式一般分为“三步”
一定:确定 ,把多项式的各项写成含公 因式的 _____的式;
二提:把公因式提到 ______ 前面,余下的项写在_____内.
三检查:检查各项的__________是否提彻底.公因式积括号公因式括号解: 注意:首项为负数时,要先变号再提公因式。当某一项和公因式相同时,提公因式后剩余的项是1.-3a2b3 +6a3b2c +3a2b -3a2b3 +6a3b2c +3a2b
= -( 3a2b3 -6a3b2c -3a2b)
= -(3a2b·b2-3a2b·2abc-3a2b·1)
=-3a2b (b2-2abc -1) 例3 分解因式: 把下列多项式分解因式:
(1)12x2y+18xy2; (2)-x2+xy-xz;
(3)2x3+6x2+2x
现有甲、乙、丙三位同学各做一题,他们的解法如下:
你认为他们的解法正确吗?试说明理由。
甲同学:
解:12x2y+18xy2
=3xy(4x+6y)乙同学:
解:-x2+xy-xz
=-x(x+y-z)丙同学:
解:2x3+6x2+2x
=2x(x2+3x)找错误 1.分解因式?2.确定公因式的方法?
一定系数 二定字母 三定指数课堂小结3、提公因式法分解因式步骤(分三步):
第一步,定公因式;
第二步,提公因式;
第三步,检查公因式是否提彻底。4、用提公因式法分解因式应注意的问题:1、公因式提取要彻底;
2、首项为负先提负;
3、提取公因式莫漏1.作业: 一定;二提;
三检查。
