等腰三角形习题课
图片预览




文档简介
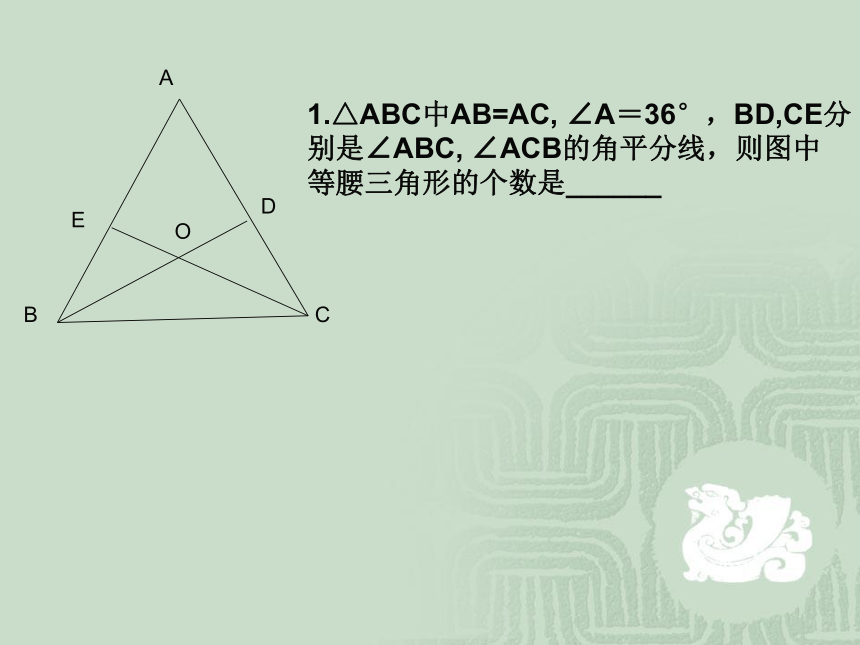
课件14张PPT。等腰三角形习题课AEBDCO1.△ABC中AB=AC, ∠A=36°,BD,CE分
别是∠ABC, ∠ACB的角平分线,则图中
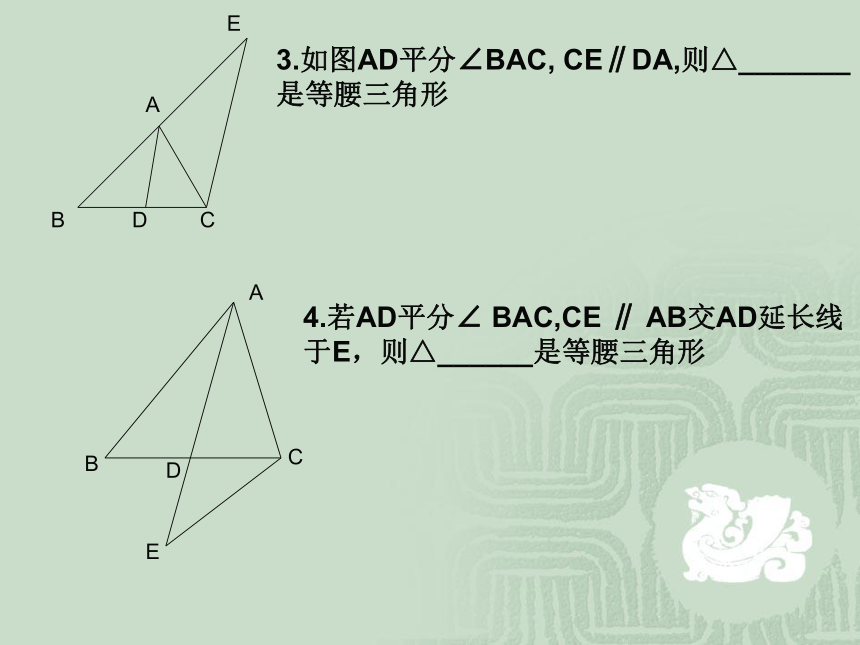
等腰三角形的个数是______EABDC3.如图AD平分∠BAC, CE∥DA,则△_______
是等腰三角形ABCDE4.若AD平分∠ BAC,CE ∥ AB交AD延长线
于E,则△______是等腰三角形例1 等腰三角形的一边长为4,另一边长为6,问
可组成几种不同的等腰三角形?(一边长为
3,另一边长为6呢?)解:当取腰长为4,则三角形三边为4,4,6当取腰长为6,则三角形三边为6,6,4(满足三角形三边关系)(满足三角形三边关系)所以可组成2种不同的三角形。当取腰长为3,则三边3,3,6(不满足三角形三边关系)当取腰长为6,则三边6,6,3(满足三角形三边关系)所以可组成1种三角形。变式1:一个等腰三角形周长为21,其中一 边长为9,
求三角形的腰长?解:当边长9为腰长,则三角形三边9,9,3当边长9为底边长,则三角形三边6,6,9(满足三边关系)(满足三边关系)所以三角形 的腰长为 9或6。变式2:已知等腰三角形的底边和一腰长是方程组
X+2Y=4
3X+Y=7 的解,求这个三角形的各边长。
解:解方程组得:X=2,Y=1当取腰长为2,则三角形三边2,2,1(满足三角形三边要求) 当取腰长为1,则三角形三边1,1,2(不满足三角形三边)所以这个三角形的边为2,2,1。变式3:已知等腰三角形一腰上的中线将三角形周
长分成2:1两部分,已知三角形底边长
为5,求腰长。解:如图,令CD=X,则AD=X,AB=2X∵底边BC=5∴BC+CD=5+X
AB+AD=3X∴(5+X):3X=2:1
或3X:(5+X)=2:1得X=1或X=10即腰长为2或202不合题意,所以腰长为20。XX2X5变式4: 一等腰三角形两边之比为3:2,周长为15cm,
则它的底边长为_____三边之比可能为3:3:2或3:2:2
情况一:三边长为 cm , cm, cm,可组成三角形情况二:三边长为 cm , cm , cm,可组成三角形CBDEOACDEAB5.O是△ABC两内角平分线BO,CO 的交点,
OD∥AB,OE∥AC,BC=5cm,则
△ODE的周长为_______6.CE平分∠ACB且CE⊥DB, ∠ DAB= ∠ DBA,
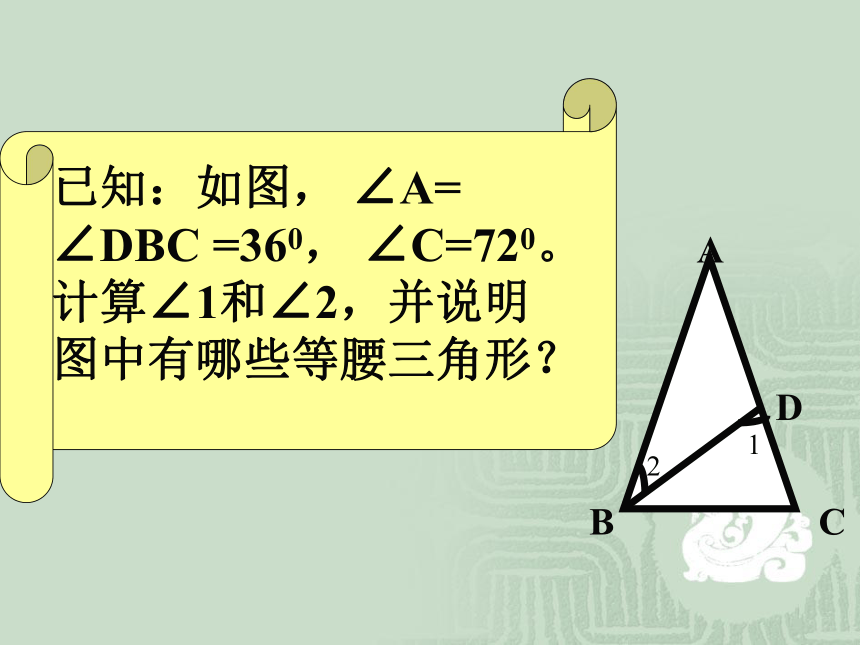
AC=18,△CDB的周长为28,则BD=_________2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)已知:如图,在△ABC中,AB=AC,
O是△ABC内一点,且OB=OC。
求证:AO⊥BCC例1例2已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE练习:已知△ABC中,AB=AC,F在AC上,在BA延长线上取
AE=AF
求证:EF⊥BCEAFBDC
别是∠ABC, ∠ACB的角平分线,则图中
等腰三角形的个数是______EABDC3.如图AD平分∠BAC, CE∥DA,则△_______
是等腰三角形ABCDE4.若AD平分∠ BAC,CE ∥ AB交AD延长线
于E,则△______是等腰三角形例1 等腰三角形的一边长为4,另一边长为6,问
可组成几种不同的等腰三角形?(一边长为
3,另一边长为6呢?)解:当取腰长为4,则三角形三边为4,4,6当取腰长为6,则三角形三边为6,6,4(满足三角形三边关系)(满足三角形三边关系)所以可组成2种不同的三角形。当取腰长为3,则三边3,3,6(不满足三角形三边关系)当取腰长为6,则三边6,6,3(满足三角形三边关系)所以可组成1种三角形。变式1:一个等腰三角形周长为21,其中一 边长为9,
求三角形的腰长?解:当边长9为腰长,则三角形三边9,9,3当边长9为底边长,则三角形三边6,6,9(满足三边关系)(满足三边关系)所以三角形 的腰长为 9或6。变式2:已知等腰三角形的底边和一腰长是方程组
X+2Y=4
3X+Y=7 的解,求这个三角形的各边长。
解:解方程组得:X=2,Y=1当取腰长为2,则三角形三边2,2,1(满足三角形三边要求) 当取腰长为1,则三角形三边1,1,2(不满足三角形三边)所以这个三角形的边为2,2,1。变式3:已知等腰三角形一腰上的中线将三角形周
长分成2:1两部分,已知三角形底边长
为5,求腰长。解:如图,令CD=X,则AD=X,AB=2X∵底边BC=5∴BC+CD=5+X
AB+AD=3X∴(5+X):3X=2:1
或3X:(5+X)=2:1得X=1或X=10即腰长为2或202不合题意,所以腰长为20。XX2X5变式4: 一等腰三角形两边之比为3:2,周长为15cm,
则它的底边长为_____三边之比可能为3:3:2或3:2:2
情况一:三边长为 cm , cm, cm,可组成三角形情况二:三边长为 cm , cm , cm,可组成三角形CBDEOACDEAB5.O是△ABC两内角平分线BO,CO 的交点,
OD∥AB,OE∥AC,BC=5cm,则
△ODE的周长为_______6.CE平分∠ACB且CE⊥DB, ∠ DAB= ∠ DBA,
AC=18,△CDB的周长为28,则BD=_________2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)已知:如图,在△ABC中,AB=AC,
O是△ABC内一点,且OB=OC。
求证:AO⊥BCC例1例2已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE练习:已知△ABC中,AB=AC,F在AC上,在BA延长线上取
AE=AF
求证:EF⊥BCEAFBDC
